6-dimensional hypercube
6-cube
Hexeract
|
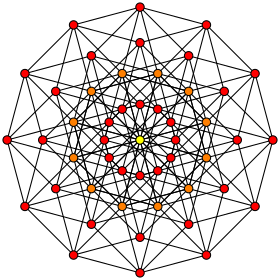
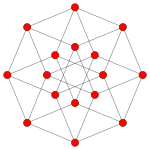
Orthogonal projection
inside Petrie polygon
Orange vertices are doubled, and the center yellow has 4 vertices
|
| Type |
Regular 6-polytope
|
| Family |
hypercube
|
| Schläfli symbol |
{4,34}
|
| Coxeter diagram |
          
|
| 5-faces |
12 {4,3,3,3} 
|
| 4-faces |
60 {4,3,3} 
|
| Cells |
160 {4,3} 
|
| Faces |
240 {4} 
|
| Edges |
192
|
| Vertices |
64
|
| Vertex figure |
5-simplex
|
| Petrie polygon |
dodecagon
|
| Coxeter group |
B6, [34,4]
|
| Dual |
6-orthoplex 
|
| Properties |
convex, Hanner polytope
|
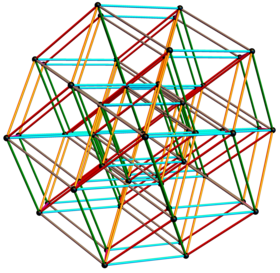
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.
It has Schläfli symbol {4,34}, being composed of 3 5-cubes around each 4-face. It can be called a hexeract, a portmanteau of tesseract (the 4-cube) with hex for six (dimensions) in Greek. It can also be called a regular dodeca-6-tope or dodecapeton, being a 6-dimensional polytope constructed from 12 regular facets.
As a configuration
This configuration matrix represents the 6-cube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]

Cartesian coordinates
Cartesian coordinates for the vertices of a 6-cube centered at the origin and edge length 2 are
- (±1,±1,±1,±1,±1,±1)
while the interior of the same consists of all points (x0, x1, x2, x3, x4, x5) with −1 < xi < 1.
Construction
There are three Coxeter groups associated with the 6-cube, one regular, with the C6 or [4,3,3,3,3] Coxeter group, and a half symmetry (D6) or [33,1,1] Coxeter group. The lowest symmetry construction is based on hyperrectangles or proprisms, cartesian products of lower dimensional hypercubes.
| Name
|
Coxeter
|
Schläfli
|
Symmetry
|
Order
|
| Regular 6-cube
|
          
          
|
{4,3,3,3,3}
|
[4,3,3,3,3] |
46080
|
| Quasiregular 6-cube
|
        
|
|
[3,3,3,31,1] |
23040
|
| hyperrectangle
|
          
|
{4,3,3,3}×{} |
[4,3,3,3,2] |
7680
|
          
|
{4,3,3}×{4} |
[4,3,3,2,4] |
3072
|
          
|
{4,3}2 |
[4,3,2,4,3] |
2304
|
          
|
{4,3,3}×{}2 |
[4,3,3,2,2] |
1536
|
          
|
{4,3}×{4}×{} |
[4,3,2,4,2] |
768
|
          
|
{4}3 |
[4,2,4,2,4] |
512
|
          
|
{4,3}×{}3 |
[4,3,2,2,2] |
384
|
          
|
{4}2×{}2 |
[4,2,4,2,2] |
256
|
          
|
{4}×{}4 |
[4,2,2,2,2] |
128
|
          
|
{}6
|
[2,2,2,2,2] |
64
|