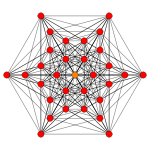
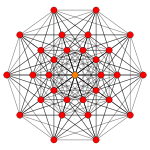
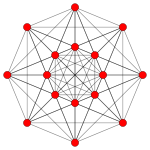
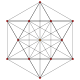
Demihexeract
(6-demicube)
|
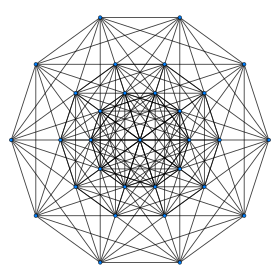
Petrie polygon projection
|
| Type
|
Uniform 6-polytope
|
| Family
|
demihypercube
|
| Schläfli symbol
|
{3,33,1} = h{4,34}
s{21,1,1,1,1}
|
| Coxeter diagrams
|
         = =           
     = =     
          
          
          
          
          
|
| Coxeter symbol
|
131
|
| 5-faces |
44 |
12 {31,2,1}
32 {34}
|
| 4-faces |
252 |
60 {31,1,1}
192 {33}
|
| Cells |
640 |
160 {31,0,1}
480 {3,3}
|
| Faces |
640 |
{3}
|
| Edges |
240
|
| Vertices |
32
|
| Vertex figure
|
Rectified 5-simplex

|
| Symmetry group
|
D6, [33,1,1] = [1+,4,34]
[25]+
|
| Petrie polygon
|
decagon
|
| Properties
|
convex
|
In geometry, a 6-demicube or demihexeract is a uniform 6-polytope, constructed from a 6-cube (hexeract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM6 for a 6-dimensional half measure polytope.
Coxeter named this polytope as 131 from its Coxeter diagram, with a ring on one of the 1-length branches, 







 . It can named similarly by a 3-dimensional exponential Schläfli symbol
. It can named similarly by a 3-dimensional exponential Schläfli symbol  or {3,33,1}.
or {3,33,1}.
Cartesian coordinates
Cartesian coordinates for the vertices of a demihexeract centered at the origin are alternate halves of the hexeract:
- (±1,±1,±1,±1,±1,±1)
with an odd number of plus signs.
As a configuration
This configuration matrix represents the 6-demicube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-demicube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[3]
| D6 |
         |
k-face |
fk |
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
k-figure |
notes
|
| A4 |
         |
( )
|
f0
|
32 |
15 |
60 |
20 |
60 |
15 |
30 |
6 |
6 |
r{3,3,3,3} |
D6/A4 = 32*6!/5! = 32
|
| A3A1A1 |
         |
{ }
|
f1
|
2 |
240 |
8 |
4 |
12 |
6 |
8 |
4 |
2 |
{}x{3,3} |
D6/A3A1A1 = 32*6!/4!/2/2 = 240
|
| A3A2 |
         |
{3}
|
f2
|
3 |
3 |
640 |
1 |
3 |
3 |
3 |
3 |
1 |
{3}v( ) |
D6/A3A2 = 32*6!/4!/3! = 640
|
| A3A1 |
         |
h{4,3}
|
f3
|
4 |
6 |
4 |
160 |
* |
3 |
0 |
3 |
0 |
{3} |
D6/A3A1 = 32*6!/4!/2 = 160
|
| A3A2 |
         |
{3,3}
|
4 |
6 |
4 |
* |
480 |
1 |
2 |
2 |
1 |
{}v( ) |
D6/A3A2 = 32*6!/4!/3! = 480
|
| D4A1 |
         |
h{4,3,3}
|
f4
|
8 |
24 |
32 |
8 |
8 |
60 |
* |
2 |
0 |
{ } |
D6/D4A1 = 32*6!/8/4!/2 = 60
|
| A4 |
         |
{3,3,3}
|
5 |
10 |
10 |
0 |
5 |
* |
192 |
1 |
1 |
D6/A4 = 32*6!/5! = 192
|
| D5 |
         |
h{4,3,3,3}
|
f5
|
16 |
80 |
160 |
40 |
80 |
10 |
16 |
12 |
* |
( ) |
D6/D5 = 32*6!/16/5! = 12
|
| A5 |
         |
{3,3,3,3}
|
6 |
15 |
20 |
0 |
15 |
0 |
6 |
* |
32 |
D6/A5 = 32*6!/6! = 32
|
Related polytopes
There are 47 uniform polytopes with D6 symmetry, 31 are shared by the B6 symmetry, and 16 are unique:
| D6 polytopes
|

h{4,34}
|

h2{4,34}
|

h3{4,34}
|

h4{4,34}
|

h5{4,34}
|

h2,3{4,34}
|

h2,4{4,34}
|

h2,5{4,34}
|

h3,4{4,34}
|

h3,5{4,34}
|

h4,5{4,34}
|

h2,3,4{4,34}
|

h2,3,5{4,34}
|

h2,4,5{4,34}
|

h3,4,5{4,34}
|
h2,3,4,5{4,34}
|
The 6-demicube, 131 is third in a dimensional series of uniform polytopes, expressed by Coxeter as k31 series. The fifth figure is a Euclidean honeycomb, 331, and the final is a noncompact hyperbolic honeycomb, 431. Each progressive uniform polytope is constructed from the previous as its vertex figure.
k31 dimensional figures
| n
|
4
|
5
|
6
|
7
|
8
|
9
|
Coxeter
group
|
A3A1
|
A5
|
D6
|
E7
|
 = E7+ = E7+
|
 =E7++ =E7++
|
Coxeter
diagram
|
      
|
      
|
        
|
          
|
            
|
              
|
| Symmetry
|
[3−1,3,1]
|
[30,3,1]
|
[31,3,1]
|
[32,3,1]
|
[33,3,1]
|
[34,3,1]
|
| Order
|
48
|
720
|
23,040
|
2,903,040
|
∞
|
| Graph
|

|
|

|

|
-
|
-
|
| Name
|
−131
|
031
|
131
|
231
|
331
|
431
|
It is also the second in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 13k series. The fourth figure is the Euclidean honeycomb 133 and the final is a noncompact hyperbolic honeycomb, 134.
13k dimensional figures
| Space
|
Finite
|
Euclidean
|
Hyperbolic
|
| n
|
4
|
5
|
6
|
7
|
8
|
9
|
Coxeter
group
|
A3A1
|
A5
|
D6
|
E7
|
 =E7+ =E7+
|
 =E7++ =E7++
|
Coxeter
diagram
|
      
|
|
        
|
          
|
            
|
              
|
| Symmetry
|
[3−1,3,1]
|
[30,3,1]
|
[31,3,1]
|
[32,3,1]
|
[[33,3,1]]
|
[34,3,1]
|
| Order
|
48
|
720
|
23,040
|
2,903,040
|
∞
|
| Graph
|
|

|

|

|
-
|
-
|
| Name
|
13,-1
|
130
|
131
|
132
|
133
|
134
|
Skew icosahedron
Coxeter identified a subset of 12 vertices that form a regular skew icosahedron {3, 5} with the same symmetries as the icosahedron itself, but at different angles. He dubbed this the regular skew icosahedron.[4][5]

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . It can named similarly by a 3-dimensional exponential Schläfli symbol or {3,33,1}.
. It can named similarly by a 3-dimensional exponential Schläfli symbol or {3,33,1}.