ARGUS

Probability density function c = 1.
Cumulative distribution function c = 1.
Parameters	${\displaystyle c>0}$ cut-off (real) ${\displaystyle \chi >0}$ curvature (real)
Support	${\displaystyle x\in (0,c)\!}$
PDF	see text
CDF	see text
Mean	${\displaystyle \mu =c{\sqrt {\pi /8))\;{\frac {\chi e^{-{\frac {\chi ^{2)){4))}I_{1}({\tfrac {\chi ^{2)){4)))}{\Psi (\chi )))}$ where I1 is the Modified Bessel function of the first kind of order 1, and ${\displaystyle \Psi (x)}$ is given in the text.
Mode	${\displaystyle {\frac {c}((\sqrt {2))\chi )){\sqrt {(\chi ^{2}-2)+{\sqrt {\chi ^{4}+4))))}$
Variance	${\displaystyle c^{2}\!\left(1-{\frac {3}{\chi ^{2))}+{\frac {\chi \phi (\chi )}{\Psi (\chi )))\right)-\mu ^{2))$

In physics, the ARGUS distribution, named after the particle physics experiment ARGUS,^[1] is the probability distribution of the reconstructed invariant mass of a decayed particle candidate^{[clarification needed]} in continuum background^{[clarification needed]}.

Definition

The probability density function (pdf) of the ARGUS distribution is:

${\displaystyle f(x;\chi ,c)={\frac {\chi ^{3))((\sqrt {2\pi ))\,\Psi (\chi )))\cdot {\frac {x}{c^{2))}{\sqrt {1-{\frac {x^{2)){c^{2))))}\exp {\bigg \{}-{\frac {1}{2))\chi ^{2}{\Big (}1-{\frac {x^{2)){c^{2))}{\Big )}{\bigg \)),}$

for ${\displaystyle 0\leq x<c}$. Here ${\displaystyle \chi }$ and ${\displaystyle c}$ are parameters of the distribution and

${\displaystyle \Psi (\chi )=\Phi (\chi )-\chi \phi (\chi )-{\tfrac {1}{2)),}$

where ${\displaystyle \Phi (x)}$ and ${\displaystyle \phi (x)}$ are the cumulative distribution and probability density functions of the standard normal distribution, respectively.

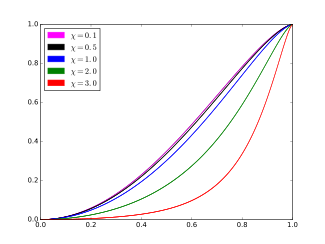
Cumulative distribution function

The cumulative distribution function (cdf) of the ARGUS distribution is

${\displaystyle F(x)=1-{\frac {\Psi \left(\chi {\sqrt {1-x^{2}/c^{2))}\right)}{\Psi (\chi )))}$.

Parameter estimation

Parameter c is assumed to be known (the kinematic limit of the invariant mass distribution), whereas χ can be estimated from the sample X₁, …, X_n using the maximum likelihood approach. The estimator is a function of sample second moment, and is given as a solution to the non-linear equation

${\displaystyle 1-{\frac {3}{\chi ^{2))}+{\frac {\chi \phi (\chi )}{\Psi (\chi )))={\frac {1}{n))\sum _{i=1}^{n}{\frac {x_{i}^{2)){c^{2))))$.

The solution exists and is unique, provided that the right-hand side is greater than 0.4; the resulting estimator ${\displaystyle \scriptstyle {\hat {\chi ))}$ is consistent and asymptotically normal.

Generalized ARGUS distribution

Sometimes a more general form is used to describe a more peaking-like distribution:

${\displaystyle f(x)={\frac {2^{-p}\chi ^{2(p+1))){\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2))\chi ^{2})))\cdot {\frac {x}{c^{2))}\left(1-{\frac {x^{2)){c^{2))}\right)^{p}\exp \left\{-{\frac {1}{2))\chi ^{2}\left(1-{\frac {x^{2)){c^{2))}\right)\right\},\qquad 0\leq x\leq c,\qquad c>0,\,\chi >0,\,p>-1}$

${\displaystyle F(x)={\frac {\Gamma \left(p+1,\,{\tfrac {1}{2))\chi ^{2}\left(1-{\frac {x^{2)){c^{2))}\right)\right)-\Gamma (p+1,\,{\tfrac {1}{2))\chi ^{2})}{\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2))\chi ^{2}))),\qquad 0\leq x\leq c,\qquad c>0,\,\chi >0,\,p>-1}$

where Γ(·) is the gamma function, and Γ(·,·) is the upper incomplete gamma function.

Here parameters c, χ, p represent the cutoff, curvature, and power respectively.

The mode is:

${\displaystyle {\frac {c}((\sqrt {2))\chi )){\sqrt {(\chi ^{2}-2p-1)+{\sqrt {\chi ^{2}(\chi ^{2}-4p+2)+(1+2p)^{2))))))$

The mean is:

${\displaystyle \mu =c\,p\,{\sqrt {\pi )){\frac {\Gamma (p)}{\Gamma ({\tfrac {5}{2))+p))){\frac {\chi ^{2p+2)){2^{p+2))}{\frac {M\left(p+1,{\tfrac {5}{2))+p,-{\tfrac {\chi ^{2)){2))\right)}{\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2))\chi ^{2})))}$

where M(·,·,·) is the Kummer's confluent hypergeometric function.^{[2][circular reference]}

The variance is:

${\displaystyle \sigma ^{2}=c^{2}{\frac {\left({\frac {\chi }{2))\right)^{p+1}\chi ^{p+3}e^{-{\tfrac {\chi ^{2)){2))}+\left(\chi ^{2}-2(p+1)\right)\left\{\Gamma (p+2)-\Gamma (p+2,\,{\tfrac {1}{2))\chi ^{2})\right\)){\chi ^{2}(p+1)\left(\Gamma (p+1)-\Gamma (p+1,\,{\tfrac {1}{2))\chi ^{2})\right)))-\mu ^{2))$

p = 0.5 gives a regular ARGUS, listed above.