 The title page of the original 1879 edition | |
| Author | Gottlob Frege |
|---|---|
| Language | English |
| Genre | Logic |
| Publisher | Lubrecht & Cramer |
Publication date | 1879 |
| Pages | 124 |
| ISBN | 978-3487-0062-39 |
| OCLC | 851287 |
Begriffsschrift (German for, roughly, "concept-writing") is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book.
Begriffsschrift is usually translated as concept writing or concept notation; the full title of the book identifies it as "a formula language, modeled on that of arithmetic, for pure thought." Frege's motivation for developing his formal approach to logic resembled Leibniz's motivation for his calculus ratiocinator (despite that, in the foreword Frege clearly denies that he achieved this aim, and also that his main aim would be constructing an ideal language like Leibniz's, which Frege declares to be a quite hard and idealistic—though not impossible—task). Frege went on to employ his logical calculus in his research on the foundations of mathematics, carried out over the next quarter-century. This is the first work in Analytical Philosophy, a field that future British and Anglo philosophers such as Bertrand Russell further developed.
The calculus contains the first appearance of quantified variables, and is essentially classical bivalent second-order logic with identity. It is bivalent in that sentences or formulas denote either True or False; second order because it includes relation variables in addition to object variables and allows quantification over both. The modifier "with identity" specifies that the language includes the identity relation, =. Frege stated that his book was his version of a characteristica universalis, a Leibnizian concept that would be applied in mathematics.[1]
Frege presents his calculus using idiosyncratic two-dimensional notation: connectives and quantifiers are written using lines connecting formulas, rather than the symbols ¬, ∧, and ∀ in use today. For example, that judgement B materially implies judgement A, i.e. is written as ![]() .
.
In the first chapter, Frege defines basic ideas and notation, like proposition ("judgement"), the universal quantifier ("the generality"), the conditional, negation and the "sign for identity of content" (which he used to indicate both material equivalence and identity proper); in the second chapter he declares nine formalized propositions as axioms.
| Basic concept | Frege's notation | Modern notations |
|---|---|---|
| Judging |
| |
| Negation |
| |
| Conditional (implication) | 
|
|
| Universal quantification | ||
| Existential quantification | ||
| Content identity (equivalence/identity) |
|
In chapter 1, §5, Frege defines the conditional as follows:
Let
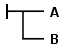
signify that the third of those possibilities does not obtain, but one of the three others does. So if we negate 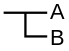 ,
that means the third possibility is valid, i.e. we negate A and assert B."
,
that means the third possibility is valid, i.e. we negate A and assert B."
Frege declared nine of his propositions to be axioms, and justified them by arguing informally that, given their intended meanings, they express self-evident truths. Re-expressed in contemporary notation, these axioms are:
These are propositions 1, 2, 8, 28, 31, 41, 52, 54, and 58 in the Begriffschrifft. (1)–(3) govern material implication, (4)–(6) negation, (7) and (8) identity, and (9) the universal quantifier. (7) expresses Leibniz's indiscernibility of identicals, and (8) asserts that identity is a reflexive relation.
All other propositions are deduced from (1)–(9) by invoking any of the following inference rules:
The main results of the third chapter, titled "Parts from a general series theory," concern what is now called the ancestral of a relation R. "a is an R-ancestor of b" is written "aR*b".
Frege applied the results from the Begriffsschrifft, including those on the ancestral of a relation, in his later work The Foundations of Arithmetic. Thus, if we take xRy to be the relation y = x + 1, then 0R*y is the predicate "y is a natural number." (133) says that if x, y, and z are natural numbers, then one of the following must hold: x < y, x = y, or y < x. This is the so-called "law of trichotomy".
For a careful recent study of how the Begriffsschrift was reviewed in the German mathematical literature, see Vilko (1998). Some reviewers, especially Ernst Schröder, were on the whole favorable. All work in formal logic subsequent to the Begriffsschrift is indebted to it, because its second-order logic was the first formal logic capable of representing a fair bit of mathematics and natural language.
Some vestige of Frege's notation survives in the "turnstile" symbol derived from his "Urteilsstrich" (judging/inferring stroke) │ and "Inhaltsstrich" (i.e. content stroke) ──. Frege used these symbols in the Begriffsschrift in the unified form ├─ for declaring that a proposition is true. In his later "Grundgesetze" he revises slightly his interpretation of the ├─ symbol.
In "Begriffsschrift" the "Definitionsdoppelstrich" (i.e. definition double stroke) │├─ indicates that a proposition is a definition. Furthermore, the negation sign can be read as a combination of the horizontal Inhaltsstrich with a vertical negation stroke. This negation symbol was reintroduced by Arend Heyting[2] in 1930 to distinguish intuitionistic from classical negation. It also appears in Gerhard Gentzen's doctoral dissertation.
In the Tractatus Logico Philosophicus, Ludwig Wittgenstein pays homage to Frege by employing the term Begriffsschrift as a synonym for logical formalism.
Frege's 1892 essay, "On Sense and Reference," recants some of the conclusions of the Begriffsschrifft about identity (denoted in mathematics by the "=" sign). In particular, he rejects the "Begriffsschrift" view that the identity predicate expresses a relationship between names, in favor of the conclusion that it expresses a relationship between the objects that are denoted by those names.
Translations: