Category of Relations Rel.
In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.
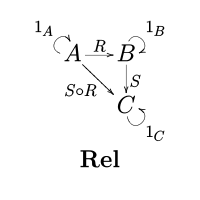
A morphism (or arrow) R : A → B in this category is a relation between the sets A and B, so R ⊆ A × B.
The composition of two relations R: A → B and S: B → C is given by
- (a, c) ∈ S o R ⇔ for some b ∈ B, (a, b) ∈ R and (b, c) ∈ S.[1]
Rel has also been called the "category of correspondences of sets".[2]
Properties
The category Rel has the category of sets Set as a (wide) subcategory, where the arrow f : X → Y in Set corresponds to the relation F ⊆ X × Y defined by (x, y) ∈ F ⇔ f(x) = y.[note 1][3]
A morphism in Rel is a relation, and the corresponding morphism in the opposite category to Rel has arrows reversed, so it is the converse relation. Thus Rel contains its opposite and is self-dual.[4]
The involution represented by taking the converse relation provides the dagger to make Rel a dagger category.
The category has two functors into itself given by the hom functor: A binary relation R ⊆ A × B and its transpose RT ⊆ B × A may be composed either as R RT or as RT R. The first composition results in a homogeneous relation on A and the second is on B. Since the images of these hom functors are in Rel itself, in this case hom is an internal hom functor. With its internal hom functor, Rel is a closed category, and furthermore a dagger compact category.
The category Rel can be obtained from the category Set as the Kleisli category for the monad whose functor corresponds to power set, interpreted as a covariant functor.
Perhaps a bit surprising at first sight is the fact that product in Rel is given by the disjoint union[4]: 181 (rather than the cartesian product as it is in Set), and so is the coproduct.
Rel is monoidal closed, if one defines both the monoidal product A ⊗ B and the internal hom A ⇒ B by the cartesian product of sets. It is also a monoidal category if one defines the monoidal product by the disjoint union of sets.[5]
The category Rel was the prototype for the algebraic structure called an allegory by Peter J. Freyd and Andre Scedrov in 1990.[6] Starting with a regular category and a functor F: A → B, they note properties of the induced functor Rel(A,B) → Rel(FA, FB). For instance, it preserves composition, conversion, and intersection. Such properties are then used to provide axioms for an allegory.
Relations as objects
David Rydeheard and Rod Burstall consider Rel to have objects that are homogeneous relations. For example, A is a set and R ⊆ A × A is a binary relation on A. The morphisms of this category are functions between sets that preserve a relation: Say S ⊆ B × B is a second relation and f: A → B is a function such that  then f is a morphism.[7]
then f is a morphism.[7]
The same idea is advanced by Adamek, Herrlich and Strecker, where they designate the objects (A, R) and (B, S), set and relation.[8]