
In cryptography, a cipher (or cypher) is an algorithm for performing encryption or decryption—a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. To encipher or encode is to convert information into cipher or code. In common parlance, "cipher" is synonymous with "code", as they are both a set of steps that encrypt a message; however, the concepts are distinct in cryptography, especially classical cryptography.
Codes generally substitute different length strings of characters in the output, while ciphers generally substitute the same number of characters as are input. A code maps one meaning with another. Words and phrases can be coded as letters or numbers. Codes typically have direct meaning from input to key. Codes primarily function to save time. Ciphers are algorithmic. The given input must follow the cipher's process to be solved. Ciphers are commonly used to encrypt written information.
Codes operated by substituting according to a large codebook which linked a random string of characters or numbers to a word or phrase. For example, "UQJHSE" could be the code for "Proceed to the following coordinates." When using a cipher the original information is known as plaintext, and the encrypted form as ciphertext. The ciphertext message contains all the information of the plaintext message, but is not in a format readable by a human or computer without the proper mechanism to decrypt it.
The operation of a cipher usually depends on a piece of auxiliary information, called a key (or, in traditional NSA parlance, a cryptovariable). The encrypting procedure is varied depending on the key, which changes the detailed operation of the algorithm. A key must be selected before using a cipher to encrypt a message. Without knowledge of the key, it should be extremely difficult, if not impossible, to decrypt the resulting ciphertext into readable plaintext.
Most modern ciphers can be categorized in several ways:
Originating from the Arabic word for zero صفر (sifr), the word "cipher" spread to Europe as part of the Arabic numeral system during the Middle Ages. The Roman numeral system lacked the concept of zero, and this limited advances in mathematics. In this transition, the word was adopted into Medieval Latin as cifra, and then into Middle French as cifre. This eventually led to the English word cipher (minority spelling cypher). One theory for how the term came to refer to encoding is that the concept of zero was confusing to Europeans, and so the term came to refer to a message or communication that was not easily understood.[1]
The term cipher was later also used to refer to any Arabic digit, or to calculation using them, so encoding text in the form of Arabic numerals is literally converting the text to "ciphers".
|
Main article: Code (cryptography) |
In casual contexts, "code" and "cipher" can typically be used interchangeably; however, the technical usages of the words refer to different concepts. Codes contain meaning; words and phrases are assigned to numbers or symbols, creating a shorter message.
An example of this is the commercial telegraph code which was used to shorten long telegraph messages which resulted from entering into commercial contracts using exchanges of telegrams.
Another example is given by whole word ciphers, which allow the user to replace an entire word with a symbol or character, much like the way written Japanese utilizes Kanji (meaning Chinese characters in Japanese) characters to supplement the native Japanese characters representing syllables. An example using English language with Kanji could be to replace "The quick brown fox jumps over the lazy dog" by "The quick brown 狐 jumps 上 the lazy 犬". Stenographers sometimes use specific symbols to abbreviate whole words.
Ciphers, on the other hand, work at a lower level: the level of individual letters, small groups of letters, or, in modern schemes, individual bits and blocks of bits. Some systems used both codes and ciphers in one system, using superencipherment to increase the security. In some cases the terms codes and ciphers are used synonymously with substitution and transposition, respectively.
Historically, cryptography was split into a dichotomy of codes and ciphers, while coding had its own terminology analogous to that of ciphers: "encoding, codetext, decoding" and so on.
However, codes have a variety of drawbacks, including susceptibility to cryptanalysis and the difficulty of managing a cumbersome codebook. Because of this, codes have fallen into disuse in modern cryptography, and ciphers are the dominant technique.
There are a variety of different types of encryption. Algorithms used earlier in the history of cryptography are substantially different from modern methods, and modern ciphers can be classified according to how they operate and whether they use one or two keys.
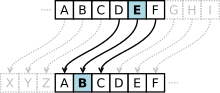
The Caesar Cipher is one of the earliest known cryptographic systems. Julius Caesar used a cipher that shifts the letters in the alphabet in place by three and wrapping the remaining letters to the front to write to Marcus Tullius Cicero in approximately 50 BC.[citation needed]
Historical pen and paper ciphers used in the past are sometimes known as classical ciphers. They include simple substitution ciphers (such as ROT13) and transposition ciphers (such as a Rail Fence Cipher). For example, "GOOD DOG" can be encrypted as "PLLX XLP" where "L" substitutes for "O", "P" for "G", and "X" for "D" in the message. Transposition of the letters "GOOD DOG" can result in "DGOGDOO". These simple ciphers and examples are easy to crack, even without plaintext-ciphertext pairs.[2][3]
In the 1640s, the Parliamentarian commander, Edward Montagu, 2nd Earl of Manchester, developed ciphers to send coded messages to his allies during the English Civil War.[4]
Simple ciphers were replaced by polyalphabetic substitution ciphers (such as the Vigenère) which changed the substitution alphabet for every letter. For example, "GOOD DOG" can be encrypted as "PLSX TWF" where "L", "S", and "W" substitute for "O". With even a small amount of known or estimated plaintext, simple polyalphabetic substitution ciphers and letter transposition ciphers designed for pen and paper encryption are easy to crack.[5] It is possible to create a secure pen and paper cipher based on a one-time pad, but these have other disadvantages.
During the early twentieth century, electro-mechanical machines were invented to do encryption and decryption using transposition, polyalphabetic substitution, and a kind of "additive" substitution. In rotor machines, several rotor disks provided polyalphabetic substitution, while plug boards provided another substitution. Keys were easily changed by changing the rotor disks and the plugboard wires. Although these encryption methods were more complex than previous schemes and required machines to encrypt and decrypt, other machines such as the British Bombe were invented to crack these encryption methods.
Modern encryption methods can be divided by two criteria: by type of key used, and by type of input data.
By type of key used ciphers are divided into:

In a symmetric key algorithm (e.g., DES and AES), the sender and receiver must have a shared key set up in advance and kept secret from all other parties; the sender uses this key for encryption, and the receiver uses the same key for decryption. The design of AES (Advanced Encryption System) was beneficial because it aimed to overcome the flaws in the design of the DES (Data encryption standard). AES's designer's claim that the common means of modern cipher cryptanalytic attacks are ineffective against AES due to its design structure.[12]
Ciphers can be distinguished into two types by the type of input data:
In a pure mathematical attack, (i.e., lacking any other information to help break a cipher) two factors above all count:
Since the desired effect is computational difficulty, in theory one would choose an algorithm and desired difficulty level, thus decide the key length accordingly.
An example of this process can be found at Key Length which uses multiple reports to suggest that a symmetrical cipher with 128 bits, an asymmetric cipher with 3072 bit keys, and an elliptic curve cipher with 256 bits, all have similar difficulty at present.
Claude Shannon proved, using information theory considerations, that any theoretically unbreakable cipher must have keys which are at least as long as the plaintext, and used only once: one-time pad.[6]