Quotient space of a codomain of a linear map by the map's image
The cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y / im(f) of the codomain of f by the image of f. The dimension of the cokernel is called the corank of f.
Cokernels are dual to the kernels of category theory, hence the name: the kernel is a subobject of the domain (it maps to the domain), while the cokernel is a quotient object of the codomain (it maps from the codomain).
Intuitively, given an equation f(x) = y that one is seeking to solve, the cokernel measures the constraints that y must satisfy for this equation to have a solution – the obstructions to a solution – while the kernel measures the degrees of freedom in a solution, if one exists. This is elaborated in intuition, below.
More generally, the cokernel of a morphism f : X → Y in some category (e.g. a homomorphism between groups or a bounded linear operator between Hilbert spaces) is an object Q and a morphism q : Y → Q such that the composition q f is the zero morphism of the category, and furthermore q is universal with respect to this property. Often the map q is understood, and Q itself is called the cokernel of f.
In many situations in abstract algebra, such as for abelian groups, vector spaces or modules, the cokernel of the homomorphism f : X → Y is the quotient of Y by the image of f. In topological settings, such as with bounded linear operators between Hilbert spaces, one typically has to take the closure of the image before passing to the quotient.
Formal definition
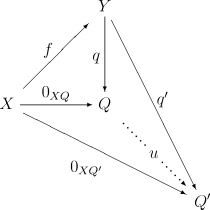
One can define the cokernel in the general framework of category theory. In order for the definition to make sense the category in question must have zero morphisms. The cokernel of a morphism f : X → Y is defined as the coequalizer of f and the zero morphism 0XY : X → Y.
Explicitly, this means the following. The cokernel of f : X → Y is an object Q together with a morphism q : Y → Q such that the diagram
commutes. Moreover, the morphism q must be universal for this diagram, i.e. any other such q′ : Y → Q′ can be obtained by composing q with a unique morphism u : Q → Q′:
As with all universal constructions the cokernel, if it exists, is unique up to a unique isomorphism, or more precisely: if q : Y → Q and q′ : Y → Q′ are two cokernels of f : X → Y, then there exists a unique isomorphism u : Q → Q′ with q' = u q.
Like all coequalizers, the cokernel q : Y → Q is necessarily an epimorphism. Conversely an epimorphism is called normal (or conormal) if it is the cokernel of some morphism. A category is called conormal if every epimorphism is normal (e.g. the category of groups is conormal).
Examples
In the category of groups, the cokernel of a group homomorphism f : G → H is the quotient of H by the normal closure of the image of f. In the case of abelian groups, since every subgroup is normal, the cokernel is just H modulo the image of f:

Special cases
In a preadditive category, it makes sense to add and subtract morphisms. In such a category, the coequalizer of two morphisms f and g (if it exists) is just the cokernel of their difference:

In an abelian category (a special kind of preadditive category) the image and coimage of a morphism f are given by

In particular, every abelian category is normal (and conormal as well). That is, every monomorphism m can be written as the kernel of some morphism. Specifically, m is the kernel of its own cokernel:

Intuition
The cokernel can be thought of as the space of constraints that an equation must satisfy, as the space of obstructions, just as the kernel is the space of solutions.
Formally, one may connect the kernel and the cokernel of a map T: V → W by the exact sequence

These can be interpreted thus: given a linear equation T(v) = w to solve,
- the kernel is the space of solutions to the homogeneous equation T(v) = 0, and its dimension is the number of degrees of freedom in solutions to T(v) = w, if they exist;
- the cokernel is the space of constraints on w that must be satisfied if the equation is to have a solution, and its dimension is the number of independent constraints that must be satisfied for the equation to have a solution.
The dimension of the cokernel plus the dimension of the image (the rank) add up to the dimension of the target space, as the dimension of the quotient space W / T(V) is simply the dimension of the space minus the dimension of the image.
As a simple example, consider the map T: R2 → R2, given by T(x, y) = (0, y). Then for an equation T(x, y) = (a, b) to have a solution, we must have a = 0 (one constraint), and in that case the solution space is (x, b), or equivalently, (0, b) + (x, 0), (one degree of freedom). The kernel may be expressed as the subspace (x, 0) ⊆ V: the value of x is the freedom in a solution. The cokernel may be expressed via the real valued map W: (a, b) → (a): given a vector (a, b), the value of a is the obstruction to there being a solution.
Additionally, the cokernel can be thought of as something that "detects" surjections in the same way that the kernel "detects" injections. A map is injective if and only if its kernel is trivial, and a map is surjective if and only if its cokernel is trivial, or in other words, if W = im(T).