
A heptatonic scale is a musical scale that has seven pitches, or tones, per octave. Examples include:
- the diatonic scale; e.g., in C major: C D E F G A B C—and in the relative minor, A minor, natural minor: A B C D E F G A
- the melodic minor scale, A B C D E F♯G♯A ascending, A G F E D C B A descending
- the harmonic minor scale, A B C D E F G♯A
- the harmonic major scale, C D E F G A♭B C.
Indian classical theory postulates seventy-two seven-tone scale types, collectively called melakarta or thaat, whereas others postulate twelve or ten (depending on the theorist) seven-tone scale types.
Several heptatonic scales in Western, Roman, Spanish, Hungarian, and Greek music can be analyzed as juxtapositions of tetrachords.[1] All heptatonic scales have all intervals present in their interval vector analysis,[2] and thus all heptatonic scales are both hemitonic and tritonic. There is a special affinity for heptatonic scales in the Western key signature system.
Diatonic scale
[edit]A diatonic scale is any seven-note scale constructed sequentially using only whole tones and half tones, repeating at the octave, having a tonal center, and comprising only one tritone interval between any two scale members, which ensures that the half tone intervals are as far apart as possible. In Western music, there are seven such scales, and they are commonly known as the modes of the major scale (Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian).
Melodic minor scale
[edit]
In traditional classical theory, the melodic minor scale has two forms, as noted above, an ascending form and a descending form. Although each of these forms of itself comprises seven pitches, together they comprise nine, which might seem to call into question the scale's status as a heptatonic scale. In certain twentieth-century music, however, it became common systematically to use the ascending form for both ascending and descending passages. Such a use has been notably ascribed to the works of Béla Bartók and to bop and post-bop jazz practice. The traditional descending form of the melodic minor scale is equivalent to the natural minor scale in both pitch collection (which is diatonic) and tonal center.
Harmonic minor scale
[edit]
The harmonic minor scale is so called because in tonal music of the common practice period (from approximately 1600 to approximately 1900) chords or harmonies are derived from it more than from the natural minor scale or the melodic minor scale. The augmented second between its sixth degree and its raised seventh degree (the "leading tone"), traditionally considered undesirable in melodic progression, is avoided by placing these pitches in different voices in adjacent chords, as in this progression: F A♭ D, F G B, F A♭ C (ii°b–V7d–iv in C minor). The A♭ in the middle voice does not ascend to B, and the B in the upper voice does not descend to A♭.
Heptatonia prima and secunda
[edit]The names heptatonia prima and heptatonia secunda apply to seven-note scales that can be formed using five tones (t) and two semi-tones (s), (also called whole-steps and half-steps), but without two semi-tones in succession. Throughout history and to the present day, some have occurred much more commonly than others, namely Ionian (also called the major scale), Aeolian (also called the natural minor scale), melodic ascending minor, Dorian, Mixolydian, Lydian, Lydian dominant, Aeolian dominant, and altered scales.
Heptatonia prima
[edit]In these scales the semi-tones are maximally separated. They are known most commonly as the diatonic modes. Beginning on keynote C and working up the notes of the 'natural minor' scale (A, B, C, D, E, F, G, A), the seven modes are:

- Aeolian mode (natural minor) t-s-t-t-s-t-t

- Locrian mode s-t-t-s-t-t-t

- Ionian mode (major) t-t-s-t-t-t-s

- Dorian mode t-s-t-t-t-s-t

- Phrygian mode s-t-t-t-s-t-t

- Lydian mode t-t-t-s-t-t-s

- Mixolydian mode t-t-s-t-t-s-t
Heptatonia secunda
[edit]While the diatonic modes have two and three tones on either side of each semitone, the heptatonia secunda modes have one and four. These are sometimes called modes of the melodic ascending minor since that is the most commonly used scale of this type, but other modes can be produced by starting on the different scale notes in turn. Thus starting on keynote A as above and following the notes of the ascending melodic minor (A, B, C, D, E, F♯, G♯) yields these seven modes:

- Ascending melodic minor scale t-s-t-t-t-t-s
- Dorian ♭2 scale or Phrygian ♯6 scale s-t-t-t-t-s-t combines the Phrygian flat second and Dorian raised sixth
- Lydian augmented scale t-t-t-t-s-t-s combines the Lydian fourth with a raised fifth
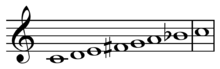
- Acoustic scale or Lydian dominant scale t-t-t-s-t-s-t So-called because it is close to the scale built on natural overtones and combines Lydian raised fourth with Mixolydian (Dominant) flat seventh
- Aeolian dominant scale or Mixolydian ♭6 scale t-t-s-t-s-t-t Like natural minor (aeolian) but with a major third

- Half diminished scale t-s-t-s-t-t-t This is like the Locrian with a raised second

- Altered scale s-t-s-t-t-t-t Like Locrian with diminished fourth
These modes are more awkward to use than those of the diatonic scales due to the four tones in a row yielding augmented intervals on one hand while the one tone between two semitones gives rise to diminished intervals on the other. For example, the last two modes listed above both have 'Locrian' diminished triads built on their tonics, giving them unstable tonality, while the third mode not only has an augmented fourth a la the Lydian mode but also an augmented fifth making the dominant and subdominant essentially unusable.
Heptatonia tertia
[edit]
The last group of seven-note tone/semitone scales is heptatonia tertia, and consists of scales with two adjacent semitones—which amounts to a whole-tone scale, but with an additional note somewhere in its sequence, e.g., B C D E F♯ G♯ A♯. One such example is the Neapolitan major scale.
Other heptatonic scales
[edit]
If the interval of the augmented second is used, many other scales become possible. These include Gypsy I-♭II-III-IV-V-♭VI-VII Hungarian I-II-♭III-♯IV-V-♭VI-VII The scales are symmetrical about the tonic and dominant respectively and the names are sometimes used interchangeably.
The double harmonic scale, also known as the Byzantine or Hungarian,[3] scale, contains the notes C D E♭ F♯ G A♭ B C.

Phrygian dominant or dominant harmonic minor I-♭II-III-IV-V-♭VI-♭VII This differs from the Phrygian in having a major third. It may also be considered built on the dominant of the harmonic minor scale.
Neapolitan minor differs from the Phrygian in having a major seventh.

Verdi's Scala Enigmatica I-♭II-III-♯IV-♯V-♯VI-VII i.e. G A♭ B C♯ D♯ E♯ F♯, which is similar to the heptatonia tertia mentioned above, differing only in that the second degree here is flattened.
Melakarta
[edit]Melakarta is a South Indian classical method of organizing Raagas based on their unique heptatonic scales. The postulated number of melakarta derives from arithmetical calculation and not from Carnatic practice, which uses far fewer scale forms. Seven-pitch melakarta are considered subsets of a twelve-pitch scale roughly analogous to the Western chromatic scale. The first and fifth melakarta tones, corresponding to the first and eighth chromatic tones, are invariable in inflection, and the fourth melakarta tone, corresponding to the sixth or seventh chromatic tone, is allowed one of two inflections only, a natural (shuddah) position and a raised (tivra) position. The second and third melakarta tones can be picked from the 4 chromatic tones (second through fifth), and similarly for the sixth and seventh. Thus the number of possible forms is equal to twice the square of the number of ways a two-membered subset can be extracted from a four-membered set:
Thaat
[edit]Hindustani heptatonic theory additionally stipulates that the second, third, sixth and seventh degrees of heptatonic scale forms (saptak) are also allowed only two inflections each, in this case, one natural position, and one lowered (komal) position. Arithmetically this produces 25, or thirty-two, possibilities, but Hindustani theory, in contradistinction to Carnatic theory, excludes scale forms not commonly used.
Chinese Gongche notation
[edit]Gongche notation heptatonic scale gives a do, re, mi, (between fa and fa♯), sol, la, (between ti♭ and ti) heptatonic scale.
See also
[edit]References
[edit]- ^ Dupré, Marcel (1962). Cours Complet d'Improvisation a l'Orgue, v.2, p. 35, trans. John Fenstermaker. Paris: Alphonse Leduc. ASIN: B0006CNH8E.
- ^ Hanson, Howard. (1960) Harmonic Materials of Modern Music, p. 362 ff. New York: Appleton-Century-Crofts. LOC 58-8138.
- ^ The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London, 2001)
| Main Western | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Other types | |||||||||||||||||||||
| Ethnic origin | |||||||||||||||||||||
| Non-octave | |||||||||||||||||||||
| Modes |
| ||||||||||||||||||||
| Number of tones |
| ||||||||||||||||||||
