Statistics
Joint probability of agreement
The joint-probability of agreement is the simplest and the least robust measure. It is estimated as the percentage of the time the raters agree in a nominal or categorical rating system. It does not take into account the fact that agreement may happen solely based on chance. There is some question whether or not there is a need to 'correct' for chance agreement; some suggest that, in any case, any such adjustment should be based on an explicit model of how chance and error affect raters' decisions.[3]
When the number of categories being used is small (e.g. 2 or 3), the likelihood for 2 raters to agree by pure chance increases dramatically. This is because both raters must confine themselves to the limited number of options available, which impacts the overall agreement rate, and not necessarily their propensity for "intrinsic" agreement (an agreement is considered "intrinsic" if it is not due to chance).
Therefore, the joint probability of agreement will remain high even in the absence of any "intrinsic" agreement among raters. A useful inter-rater reliability coefficient is expected (a) to be close to 0 when there is no "intrinsic" agreement and (b) to increase as the "intrinsic" agreement rate improves. Most chance-corrected agreement coefficients achieve the first objective. However, the second objective is not achieved by many known chance-corrected measures.[4]
Kappa statistics
|
Main articles: Cohen's kappa and Fleiss' kappa |
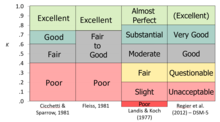
Kappa is a way of measuring agreement or reliability, correcting for how often ratings might agree by chance. Cohen's kappa,[5] which works for two raters, and Fleiss' kappa,[6] an adaptation that works for any fixed number of raters, improve upon the joint probability in that they take into account the amount of agreement that could be expected to occur through chance. The original versions had the same problem as the joint-probability in that they treat the data as nominal and assume the ratings have no natural ordering; if the data actually have a rank (ordinal level of measurement), then that information is not fully considered in the measurements.
Later extensions of the approach included versions that could handle "partial credit" and ordinal scales.[7] These extensions converge with the family of intra-class correlations (ICCs), so there is a conceptually related way of estimating reliability for each level of measurement from nominal (kappa) to ordinal (ordinal kappa or ICC—stretching assumptions) to interval (ICC, or ordinal kappa—treating the interval scale as ordinal), and ratio (ICCs). There also are variants that can look at agreement by raters across a set of items (e.g., do two interviewers agree about the depression scores for all of the items on the same semi-structured interview for one case?) as well as raters x cases (e.g., how well do two or more raters agree about whether 30 cases have a depression diagnosis, yes/no—a nominal variable).
Kappa is similar to a correlation coefficient in that it cannot go above +1.0 or below -1.0. Because it is used as a measure of agreement, only positive values would be expected in most situations; negative values would indicate systematic disagreement. Kappa can only achieve very high values when both agreement is good and the rate of the target condition is near 50% (because it includes the base rate in the calculation of joint probabilities). Several authorities have offered "rules of thumb" for interpreting the level of agreement, many of which agree in the gist even though the words are not identical.[8][9][10][11]
Correlation coefficients
|
Main articles: Pearson product-moment correlation coefficient and Spearman's rank correlation coefficient |
Either Pearson's , Kendall's τ, or Spearman's can be used to measure pairwise correlation among raters using a scale that is ordered. Pearson assumes the rating scale is continuous; Kendall and Spearman statistics assume only that it is ordinal. If more than two raters are observed, an average level of agreement for the group can be calculated as the mean of the , τ, or values from each possible pair of raters.
Intra-class correlation coefficient
|
Main article: Intra-class correlation coefficient |
Another way of performing reliability testing is to use the intra-class correlation coefficient (ICC).[12] There are several types of this and one is defined as, "the proportion of variance of an observation due to between-subject variability in the true scores".[13] The range of the ICC may be between 0.0 and 1.0 (an early definition of ICC could be between −1 and +1). The ICC will be high when there is little variation between the scores given to each item by the raters, e.g. if all raters give the same or similar scores to each of the items. The ICC is an improvement over Pearson's and Spearman's , as it takes into account the differences in ratings for individual segments, along with the correlation between raters.
Limits of agreement

Another approach to agreement (useful when there are only two raters and the scale is continuous) is to calculate the differences between each pair of the two raters' observations. The mean of these differences is termed bias and the reference interval (mean ± 1.96 × standard deviation) is termed limits of agreement. The limits of agreement provide insight into how much random variation may be influencing the ratings.
If the raters tend to agree, the differences between the raters' observations will be near zero. If one rater is usually higher or lower than the other by a consistent amount, the bias will be different from zero. If the raters tend to disagree, but without a consistent pattern of one rating higher than the other, the mean will be near zero. Confidence limits (usually 95%) can be calculated for both the bias and each of the limits of agreement.
There are several formulae that can be used to calculate limits of agreement. The simple formula, which was given in the previous paragraph and works well for sample size greater than 60,[14] is
For smaller sample sizes, another common simplification[15] is
However, the most accurate formula (which is applicable for all sample sizes)[14] is
Bland and Altman[15] have expanded on this idea by graphing the difference of each point, the mean difference, and the limits of agreement on the vertical against the average of the two ratings on the horizontal. The resulting Bland–Altman plot demonstrates not only the overall degree of agreement, but also whether the agreement is related to the underlying value of the item. For instance, two raters might agree closely in estimating the size of small items, but disagree about larger items.
When comparing two methods of measurement, it is not only of interest to estimate both bias and limits of agreement between the two methods (inter-rater agreement), but also to assess these characteristics for each method within itself. It might very well be that the agreement between two methods is poor simply because one of the methods has wide limits of agreement while the other has narrow. In this case, the method with the narrow limits of agreement would be superior from a statistical point of view, while practical or other considerations might change this appreciation. What constitutes narrow or wide limits of agreement or large or small bias is a matter of a practical assessment in each case.
Krippendorff's alpha
|
Main article: Krippendorff's alpha |
Krippendorff's alpha[16][17] is a versatile statistic that assesses the agreement achieved among observers who categorize, evaluate, or measure a given set of objects in terms of the values of a variable. It generalizes several specialized agreement coefficients by accepting any number of observers, being applicable to nominal, ordinal, interval, and ratio levels of measurement, being able to handle missing data, and being corrected for small sample sizes.
Alpha emerged in content analysis where textual units are categorized by trained coders and is used in counseling and survey research where experts code open-ended interview data into analyzable terms, in psychometrics where individual attributes are tested by multiple methods, in observational studies where unstructured happenings are recorded for subsequent analysis, and in computational linguistics where texts are annotated for various syntactic and semantic qualities.




