Examples
B20H16

m + n + o + p − q = 2 + 20 + 0 + 0 + 0 = 22 SEPs are required; 16 BH units provide 16 pairs; four shared boron atoms provide 6 pairs, which describes why B20H16 is stable as a neutral species.[7]
B21H−
18
closo-B21H−18 is formed by the face-sharing condensation of two icosahedra. The m + n + o + p − q rule demands 23 SEPs; 18 BH units provide 18 pairs and 3 shared boron atoms provide 4+1⁄2 pairs; the negative charge provides one half pair.[8]
B12H16
The bis-nido-B12H16 is formed by the edge-sharing condensation of a nido-B8 unit and a nido-B6 unit. The m + n + o + p − q count of 16 SEPs are satisfied by ten BH units which provide 10 pairs, two shared boron atoms which provide 3 pairs, and six bridging H atoms which provide 3 pairs.[7]
Cu(B11H11)3−
2
m + n + o + p − q = 26 SEPs. A transition metal with n valence electrons provides n − 6 electrons for skeletal bonding as 6 electrons occupying the metal-like orbitals do not contribute much to the cluster bonding. Therefore Cu provides 2+1⁄2 pairs, 22 BH units provide 22 pairs; three negative charges provide 1+1⁄2 pairs.[7]
Ferrocene

According to the m + n + o + p − q rule, ferrocene requires 2 + 11 + 1 + 2 − 0 = 16 SEPs. 10 CH units provide 15 pairs while Fe provides one pair. [7]
B18H2−
20
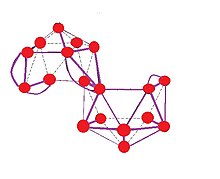
B18H2−20 is a bis-nido edge-shared polyhedron. Here, m + n + o + p − q = 2 + 18 + 0 + 2 − 0 = 22; 16 BH units provide 16 pairs, 4 bridging hydrogen atoms provide 2 pairs, two shared boron atoms provide 3 pairs, along with the two negative charges which provide 1 pair.[7]
Triple-decker complexes
Triple-decker complexes are known to obey a 30-valence electron (VE) rule. Subtracting 6 pairs of nonbonding electrons from the two metal atoms brings the number of SEPs to 9 pairs. For a triple-decker complex with C5H5 as the decks, m + n + o + p − q = 3 + 17 + 2 + 2 − 0 = 24. Subtracting the 15 pairs corresponding to C–C sigma bonds, it becomes 9 pairs. For example, consider (C5(CH3)5)3Ru+2: 15 C–CH3 groups provide 22+1⁄2 pairs. Each ruthenium atom provides one pair. Removing the electron corresponding to the positive charge of the complex leads to a total of 22+1⁄2 + 2 − 1⁄2 = 24 pairs.
β-Rhombohedral boron

The structure of β-rhombohedral boron is complicated by the presence of partial occupancies and vacancies.[9][10][11] The idealized unit cell, B105 has been shown to be electron-deficient and hence metallic according to theoretical studies, but β-boron is a semiconductor.[12] Application of the Jemmis rule shows that the partial occupancies and vacancies are necessary for electron sufficiency.
B105 can be conceptually divided into a B48 fragment and a B28−B−B28 (B57) fragment. According to Wade's rule, the B48 fragment requires 8 electrons (the icosahedron at the centre (green) requires 2 electrons; each of the six pentagonal pyramids (black and red) completes an icosahedron in the extended structure; as such the electronic requirement for each of them is 1). The B28−B−B28 or B57 is formed by the condensation of 6 icosahedra and two trigonal bipyramids. Here, m + n + o + p − q = 8 + 57 + 1 + 0 − 0 = 66 pairs required for stability, but 67+1⁄2 are available. Therefore the B28−B−B28 fragment has 3 excess electrons and the idealized B105 is missing 5 electrons. The 3 excess electrons in the B28−B−B28 fragment can be removed by removing one B atom, which leads to B27−B−B28 (B56). The requirement of 8 electrons by the B48 fragment can be satisfied by 2+2⁄3 boron atoms and the unit cell contains 48 + 56 + 2+2⁄3 = 106+2⁄3, which is very close to the experimental result.[3]