In physics, the Josephson effect is a phenomenon that occurs when two superconductors are placed in proximity, with some barrier or restriction between them. The effect is named after the British physicist Brian Josephson, who predicted in 1962 the mathematical relationships for the current and voltage across the weak link.[1][2] It is an example of a macroscopic quantum phenomenon, where the effects of quantum mechanics are observable at ordinary, rather than atomic, scale. The Josephson effect has many practical applications because it exhibits a precise relationship between different physical measures, such as voltage and frequency, facilitating highly accurate measurements.
The Josephson effect produces a current, known as a supercurrent, that flows continuously without any voltage applied, across a device known as a Josephson junction (JJ). These consist of two or more superconductors coupled by a weak link. The weak link can be a thin insulating barrier (known as a superconductor–insulator–superconductor junction, or S-I-S), a short section of non-superconducting metal (S-N-S), or a physical constriction that weakens the superconductivity at the point of contact (S-c-S).
Josephson junctions have important applications in quantum-mechanical circuits, such as SQUIDs, superconducting qubits, and RSFQ digital electronics. The NIST standard for one volt is achieved by an array of 20,208 Josephson junctions in series.[3]
History
[edit]The DC Josephson effect had been seen in experiments prior to 1962,[4] but had been attributed to "super-shorts" or breaches in the insulating barrier leading to the direct conduction of electrons between the superconductors.
In 1962, Brian Josephson became interested into superconducting tunneling. He was then 23 years old and a second-year graduate student of Brian Pippard at the Mond Laboratory of the University of Cambridge. That year, Josephson took a many-body theory course with Philip W. Anderson, a Bell Labs employee on sabbatical leave for the 1961–1962 academic year. The course introduced Josephson to the idea of broken symmetry in superconductors, and he "was fascinated by the idea of broken symmetry, and wondered whether there could be any way of observing it experimentally". Josephson studied the experiments by Ivar Giaever and Hans Meissner, and theoretical work by Robert Parmenter. Pippard initially believed that the tunneling effect was possible but that it would be too small to be noticeable, but Josephson did not agree, especially after Anderson introduced him to a preprint of "Superconductive Tunneling" by Cohen, Falicov, and Phillips about the superconductor-barrier-normal metal system.[5][6]: 223–224
Josephson and his colleagues were initially unsure about the validity of Josephson's calculations. Anderson later remembered:
We were all—Josephson, Pippard and myself, as well as various other people who also habitually sat at the Mond tea and participated in the discussions of the next few weeks—very much puzzled by the meaning of the fact that the current depends on the phase.
After further review, they concluded that Josephson's results were valid. Josephson then submitted "Possible new effects in superconductive tunnelling" to Physics Letters in June 1962[1]. The newer journal Physics Letters was chosen instead of the better established Physical Review Letters due to their uncertainty about the results. John Bardeen, by then already Nobel Prize winner, was initially publicly skeptical of Josephson's theory in 1962, but came to accept it after further experiments and theoretical clarifications.[6]: 222–227 See also: John Bardeen § Josephson Effect controversy.
In January 1963, Anderson and his Bell Labs colleague John Rowell submitted the first paper to Physical Review Letters to claim the experimental observation of Josephson's effect "Probable Observation of the Josephson Superconducting Tunneling Effect".[7] These authors were awarded patents[8] on the effects that were never enforced, but never challenged.[citation needed]
Before Josephson's prediction, it was only known that single (i.e., non-paired) electrons can flow through an insulating barrier, by means of quantum tunneling. Josephson was the first to predict the tunneling of superconducting Cooper pairs. For this work, Josephson received the Nobel Prize in Physics in 1973.[9] John Bardeen was one of the nominators.[6]: 230
Applications
[edit]
Types of Josephson junction include the φ Josephson junction (of which π Josephson junction is a special example), long Josephson junction, and superconducting tunnel junction. Other uses include:
- A "Dayem bridge" is a thin-film Josephson junction where the weak link comprises a superconducting wire measuring a few micrometres or less.[10][11]
- The Josephson junction count is a proxy variable for a device's complexity
- SQUIDs, or superconducting quantum interference devices, are very sensitive magnetometers that operate via the Josephson effect
- Superfluid helium quantum interference devices (SHeQUIDs) are the superfluid helium analog of a dc-SQUID[12]
- In precision metrology, the Josephson effect is a reproducible conversion between frequency and voltage. The Josephson voltage standard takes the caesium standard definition of frequency and gives the standard representation of a volt
- Single-electron transistors are often made from superconducting materials and called "superconducting single-electron transistors".[13]
- Elementary charge is most precisely measured in terms of the Josephson constant and the von Klitzing constant which is related to the quantum Hall effect
- RSFQ digital electronics are based on shunted Josephson junctions. Junction switching emits one magnetic flux quantum . Its presence and absence represents binary 1 and 0.
- Superconducting quantum computing uses Josephon junctions as qubits such as in a flux qubit or other schemes where the phase and charge are conjugate variables.[14]
- Superconducting tunnel junction detectors are used in superconducting cameras
The Josephson equations
[edit]
The Josephson effect can be calculated using the laws of quantum mechanics. A diagram of a single Josephson junction is shown at right. Assume that superconductor A has Ginzburg–Landau order parameter , and superconductor B , which can be interpreted as the wave functions of Cooper pairs in the two superconductors. If the electric potential difference across the junction is , then the energy difference between the two superconductors is , since each Cooper pair has twice the charge of one electron. The Schrödinger equation for this two-state quantum system is therefore:[15]
where the constant is a characteristic of the junction. To solve the above equation, first calculate the time derivative of the order parameter in superconductor A:
and therefore the Schrödinger equation gives:
The phase difference of Ginzburg–Landau order parameters across the junction is called the Josephson phase:
The Schrödinger equation can therefore be rewritten as:
and its complex conjugate equation is:
Add the two conjugate equations together to eliminate :
Since , we have:
Now, subtract the two conjugate equations to eliminate :
which gives:
Similarly, for superconductor B we can derive that:
Noting that the evolution of Josephson phase is and the time derivative of charge carrier density is proportional to current , when , the above solution yields the Josephson equations:[16]
(1)
(2)
where and are the voltage across and the current through the Josephson junction, and is a parameter of the junction named the critical current. Equation (1) is called the first Josephson relation or weak-link current-phase relation, and equation (2) is called the second Josephson relation or superconducting phase evolution equation. The critical current of the Josephson junction depends on the properties of the superconductors, and can also be affected by environmental factors like temperature and externally applied magnetic field.
The Josephson constant is defined as:
and its inverse is the magnetic flux quantum:
The superconducting phase evolution equation can be reexpressed as:
If we define:
then the voltage across the junction is:
which is very similar to Faraday's law of induction. But note that this voltage does not come from magnetic energy, since there is no magnetic field in the superconductors; Instead, this voltage comes from the kinetic energy of the carriers (i.e. the Cooper pairs). This phenomenon is also known as kinetic inductance.
Three main effects
[edit]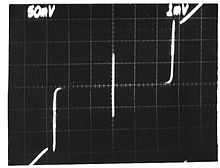
There are three main effects predicted by Josephson that follow directly from the Josephson equations:
The DC Josephson effect
[edit]The DC Josephson effect is a direct current crossing the insulator in the absence of any external electromagnetic field, owing to tunneling. This DC Josephson current is proportional to the sine of the Josephson phase (phase difference across the insulator, which stays constant over time), and may take values between and .
The AC Josephson effect
[edit]With a fixed voltage across the junction, the phase will vary linearly with time and the current will be a sinusoidal AC (alternating current) with amplitude and frequency . This means a Josephson junction can act as a perfect voltage-to-frequency converter.
The inverse AC Josephson effect
[edit]Microwave radiation of a single (angular) frequency can induce quantized DC voltages[17] across the Josephson junction, in which case the Josephson phase takes the form , and the voltage and current across the junction will be:
The DC components are:
This means a Josephson junction can act like a perfect frequency-to-voltage converter,[18] which is the theoretical basis for the Josephson voltage standard.
Josephson inductance
[edit]When the current and Josephson phase varies over time, the voltage drop across the junction will also vary accordingly; As shown in derivation below, the Josephson relations determine that this behavior can be modeled by a kinetic inductance named Josephson Inductance.[19]
Rewrite the Josephson relations as:
Now, apply the chain rule to calculate the time derivative of the current:
Rearrange the above result in the form of the current–voltage characteristic of an inductor:
This gives the expression for the kinetic inductance as a function of the Josephson Phase:
Here, is a characteristic parameter of the Josephson junction, named the Josephson Inductance.
Note that although the kinetic behavior of the Josephson junction is similar to that of an inductor, there is no associated magnetic field. This behaviour is derived from the kinetic energy of the charge carriers, instead of the energy in a magnetic field.
Josephson energy
[edit]Based on the similarity of the Josephson junction to a non-linear inductor, the energy stored in a Josephson junction when a supercurrent flows through it can be calculated.[20]
The supercurrent flowing through the junction is related to the Josephson phase by the current-phase relation (CPR):
The superconducting phase evolution equation is analogous to Faraday's law:
Assume that at time , the Josephson phase is ; At a later time , the Josephson phase evolved to . The energy increase in the junction is equal to the work done on the junction:
This shows that the change of energy in the Josephson junction depends only on the initial and final state of the junction and not the path. Therefore, the energy stored in a Josephson junction is a state function, which can be defined as:
Here is a characteristic parameter of the Josephson junction, named the Josephson Energy. It is related to the Josephson Inductance by . An alternative but equivalent definition is also often used.
Again, note that a non-linear magnetic coil inductor accumulates potential energy in its magnetic field when a current passes through it; However, in the case of Josephson junction, no magnetic field is created by a supercurrent — the stored energy comes from the kinetic energy of the charge carriers instead.
The RCSJ model
[edit]The Resistively Capacitance Shunted Junction (RCSJ) model,[21][22] or simply shunted junction model, includes the effect of AC impedance of an actual Josephson junction on top of the two basic Josephson relations stated above.
As per Thévenin's theorem,[23] the AC impedance of the junction can be represented by a capacitor and a shunt resistor, both parallel[24] to the ideal Josephson Junction. The complete expression for the current drive becomes:
where the first term is displacement current with – effective capacitance, and the third is normal current with – effective resistance of the junction.
Josephson penetration depth
[edit]The Josephson penetration depth characterizes the typical length on which an externally applied magnetic field penetrates into the long Josephson junction. It is usually denoted as and is given by the following expression (in SI):
where is the magnetic flux quantum, is the critical supercurrent density (A/m2), and characterizes the inductance of the superconducting electrodes[25]
where is the thickness of the Josephson barrier (usually insulator), and are the thicknesses of superconducting electrodes, and and are their London penetration depths. The Josephson penetration depth usually ranges from a few μm to several mm if the critical current density is very low.[26]
See also
[edit]References
[edit]- ^ a b Josephson, B. D. (1962). "Possible new effects in superconductive tunnelling". Physics Letters. 1 (7): 251–253. Bibcode:1962PhL.....1..251J. doi:10.1016/0031-9163(62)91369-0.
- ^ Josephson, B. D. (1974). "The discovery of tunnelling supercurrents". Reviews of Modern Physics. 46 (2): 251–254. Bibcode:1974RvMP...46..251J. doi:10.1103/RevModPhys.46.251. S2CID 54748764.
- Also in Josephson, B. D. (1974). "The Discovery of Tunnelling Supercurrents". Europhysics News. 5 (3): 1–5. Bibcode:1974ENews...5c...1J. doi:10.1051/epn/19740503001.
- ^ Steven Strogatz, Sync: The Emerging Science of Spontaneous Order, Hyperion, 2003.
- ^ Josephson, Brian D. (December 12, 1973). "The Discovery of Tunneling Supercurrents (Nobel Lecture)".
- ^ Cohen, M. H.; Falicov, L. M.; Phillips, J. C. (15 April 1962). "Superconductive Tunneling". Physical Review Letters. 8 (8): 316–318. Bibcode:1962PhRvL...8..316C. doi:10.1103/PhysRevLett.8.316.
- ^ a b c Daitch, Vicki; Hoddeson, Lillian (2002). True Genius: The Life and Science of John Bardeen. Joseph Henry Press. p. 117. ISBN 9780309084086.
- ^ Anderson, P. W.; Rowell, J. M. (15 March 1963). "Probable Observation of the Josephson Tunnel Effect". Physical Review Letters. 10 (6): 230. Bibcode:1963PhRvL..10..230A. doi:10.1103/PhysRevLett.10.230.
- ^ US3335363A, Anderson, Philip W. & Dayem, Aly H., "Superconductive device of varying dimension having a minimum dimension intermediate its electrodes", issued 1967-08-08
- ^ "The Nobel Prize in Physics 1973". The Nobel Prize. Retrieved 2023-03-01.
- ^ Anderson, P. W.; Dayem, A. H. (1964). "Radio-frequency effects in superconducting thin film bridges". Physical Review Letters. 13 (6): 195. Bibcode:1964PhRvL..13..195A. doi:10.1103/PhysRevLett.13.195.
- ^ Dawe, Richard (28 October 1998). "SQUIDs: A Technical Report – Part 3: SQUIDs". rich.phekda.org. Archived from the original (website) on 27 July 2011. Retrieved 2011-04-21.
- ^ Sato, Y.; Packard, R. (October 2012), Superfluid helium interferometers, Physics Today, p. 31.
- ^ Fulton, T. A.; Gammel, P. L.; Bishop, D. J.; Dunkleberger, L. N.; Dolan, G. J. (1989). "Observation of Combined Josephson and Charging Effects in Small Tunnel Junction Circuits". Physical Review Letters. 63 (12): 1307–1310. Bibcode:1989PhRvL..63.1307F. doi:10.1103/PhysRevLett.63.1307. PMID 10040529.
- ^ Bouchiat, V.; Vion, D.; Joyez, P.; Esteve, D.; Devoret, M. H. (1998). "Quantum coherence with a single Cooper pair". Physica Scripta. T76: 165. Bibcode:1998PhST...76..165B. doi:10.1238/Physica.Topical.076a00165. S2CID 250887469.
- ^ "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity, Section 21-9: The Josephson junction". feynmanlectures.caltech.edu. Retrieved 2020-01-03.
- ^ Barone, A.; Paterno, G. (1982). Physics and Applications of the Josephson Effect. New York: John Wiley & Sons. ISBN 978-0-471-01469-0.
- ^ Langenberg, D. N.; Scalapino, D. J.; Taylor, B. N.; Eck, R. E. (1966-04-01). "Microwave-induced D.C. voltages across Josephson junctions". Physics Letters. 20 (6): 563–565. Bibcode:1966PhL....20..563L. doi:10.1016/0031-9163(66)91114-0. ISSN 0031-9163.
- ^ Levinsen, M. T.; Chiao, R. Y.; Feldman, M. J.; Tucker, B. A. (1977-12-01). "An inverse ac Josephson effect voltage standard". Applied Physics Letters. 31 (11): 776–778. Bibcode:1977ApPhL..31..776L. doi:10.1063/1.89520. ISSN 0003-6951.
- ^ Devoret, M.; Wallraff, A.; Martinis, J. (2004). "Superconducting Qubits: A Short Review". arXiv:cond-mat/0411174.
- ^ Michael Tinkham, Introduction to superconductivity, Courier Corporation, 1986.
- ^ McCumber, D. E. (1968-06-01). "Effect of ac Impedance on dc Voltage-Current Characteristics of Superconductor Weak-Link Junctions". Journal of Applied Physics. 39 (7): 3113–3118. Bibcode:1968JAP....39.3113M. doi:10.1063/1.1656743. ISSN 0021-8979.
- ^ Chakravarty, Sudip; Ingold, Gert-Ludwig; Kivelson, Steven; Zimanyi, Gergely (1988-03-01). "Quantum statistical mechanics of an array of resistively shunted Josephson junctions". Physical Review B. 37 (7): 3283–3294. Bibcode:1988PhRvB..37.3283C. doi:10.1103/PhysRevB.37.3283. PMID 9944915.
- ^ "AC Thevenin's Theorem". hyperphysics.phy-astr.gsu.edu. Retrieved 2020-01-03.
- ^ "Dynamics of RF SQUID". phelafel.technion.ac.il. Archived from the original on 2021-06-13. Retrieved 2020-01-11.
- ^ Weihnacht, M. (1969). "Influence of Film Thickness on D. C. Josephson Current". Physica Status Solidi B. 32 (2): 169. Bibcode:1969PSSBR..32..169W. doi:10.1002/pssb.19690320259.
- ^ Buckel, Werner; Kleiner, Reinhold (2004). Supraleitung (6. ed.). Tübingen: Wiley-VCH Verlag GmbH&Co.KGaA. p. 67. ISBN 3527403485.
| States of matter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Phase phenomena | |||||||||
| Electrons in solids |
| ||||||||
| Magnetic phases | |||||||||
| Quasiparticles | |||||||||
| Soft matter | |||||||||
| Theories | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Characteristic parameters | |||||||||
| Phenomena | |||||||||
| Classification |
| ||||||||
| Technological applications | |||||||||
| List of superconductors | |||||||||































![{\displaystyle {\frac {\partial \varphi }{\partial t))=2\pi [K_{J}V(t)]={\frac {2\pi }{\Phi _{0))}V(t)\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a4d19b714169b822a4cda059cb835a84303f25)