
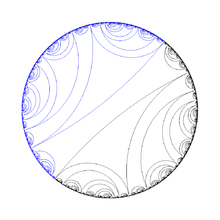
In topology, a branch of mathematics, a lamination is a :
- "topological space partitioned into subsets"[1]
- decoration (a structure or property at a point) of a manifold in which some subset of the manifold is partitioned into sheets of some lower dimension, and the sheets are locally parallel.
A lamination of a surface is a partition of a closed subset of the surface into smooth curves.
It may or may not be possible to fill the gaps in a lamination to make a foliation.[2]
