Statistical distribution
The Nakagami distribution or the Nakagami-m distribution is a probability distribution related to the gamma distribution. It is used to model physical phenomena, such as those found in medical ultrasound imaging, communications engineering, meteorology, hydrology, multimedia, and seismology.
The family of Nakagami distributions has two parameters: a shape parameter  and a second parameter controlling spread
and a second parameter controlling spread  .
.
Characterization
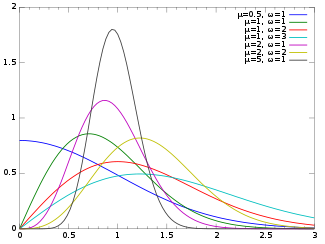
Its probability density function (pdf) is[1]

where  and
and  .
.
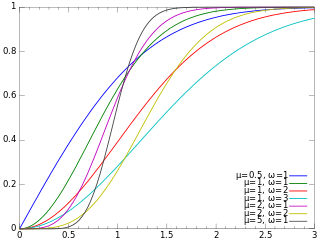
Its cumulative distribution function (CDF) is[1]

where P is the regularized (lower) incomplete gamma function.
Parameter estimation
An alternative way of fitting the distribution is to re-parametrize  as σ = Ω/m.[3]
as σ = Ω/m.[3]
Given independent observations  from the Nakagami distribution, the likelihood function is
from the Nakagami distribution, the likelihood function is

Its logarithm is

Therefore

These derivatives vanish only when

and the value of m for which the derivative with respect to m vanishes is found by numerical methods including the Newton–Raphson method.
It can be shown that at the critical point a global maximum is attained, so the critical point is the maximum-likelihood estimate of (m,σ). Because of the equivariance of maximum-likelihood estimation, a maximum likelihood estimate for Ω is obtained as well.
Random variate generation
The Nakagami distribution is related to the gamma distribution.
In particular, given a random variable  , it is possible to obtain a random variable
, it is possible to obtain a random variable  , by setting
, by setting  ,
,  , and taking the square root of
, and taking the square root of  :
:

Alternatively, the Nakagami distribution  can be generated from the chi distribution with parameter
can be generated from the chi distribution with parameter  set to
set to  and then following it by a scaling transformation of random variables. That is, a Nakagami random variable
and then following it by a scaling transformation of random variables. That is, a Nakagami random variable  is generated by a simple scaling transformation on a Chi-distributed random variable
is generated by a simple scaling transformation on a Chi-distributed random variable  as below.
as below.

For a Chi-distribution, the degrees of freedom  must be an integer, but for Nakagami the
must be an integer, but for Nakagami the  can be any real number greater than 1/2. This is the critical difference and accordingly, Nakagami-m is viewed as a generalization of Chi-distribution, similar to a gamma distribution being considered as a generalization of Chi-squared distributions.
can be any real number greater than 1/2. This is the critical difference and accordingly, Nakagami-m is viewed as a generalization of Chi-distribution, similar to a gamma distribution being considered as a generalization of Chi-squared distributions.
History and applications
The Nakagami distribution is relatively new, being first proposed in 1960 by Minoru Nakagami as a mathematical model for small-scale fading in long-distance high-frequency radio wave propagation.[4] It has been used to model attenuation of wireless signals traversing multiple paths[5] and to study the impact of fading channels on wireless communications.[6]














![{\displaystyle m={\frac {\left(\operatorname {E} \left[X^{2}\right]\right)^{2)){\operatorname {Var} \left[X^{2}\right])),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/170a63e920349b6d319032d3714dd0f6eda4655d)
![{\displaystyle \Omega =\operatorname {E} \left[X^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24eb21fa6e972b1338b50769c409be9d9f4f7129)


















