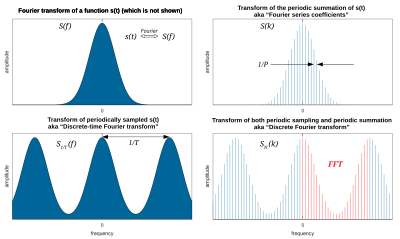
In mathematics, any integrable function can be made into a periodic function with period P by summing the translations of the function by integer multiples of P. This is called periodic summation:
When is alternatively represented as a Fourier series, the Fourier coefficients are equal to the values of the continuous Fourier transform, at intervals of .[1][2] That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of at constant intervals (T) is equivalent to a periodic summation of which is known as a discrete-time Fourier transform.
The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.










