Mathematical concept
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane curves.
Plane curves also include the Jordan curves (curves that enclose a region of the plane but need not be smooth) and the graphs of continuous functions.
Symbolic representation
A plane curve can often be represented in Cartesian coordinates by an implicit equation of the form  for some specific function f. If this equation can be solved explicitly for y or x – that is, rewritten as
for some specific function f. If this equation can be solved explicitly for y or x – that is, rewritten as  or
or  for specific function g or h – then this provides an alternative, explicit, form of the representation. A plane curve can also often be represented in Cartesian coordinates by a parametric equation of the form
for specific function g or h – then this provides an alternative, explicit, form of the representation. A plane curve can also often be represented in Cartesian coordinates by a parametric equation of the form  for specific functions
for specific functions  and
and 
Plane curves can sometimes also be represented in alternative coordinate systems, such as polar coordinates that express the location of each point in terms of an angle and a distance from the origin.
Algebraic plane curve
An algebraic plane curve is a curve in an affine or projective plane given by one polynomial equation  (or
(or  where F is a homogeneous polynomial, in the projective case.)
where F is a homogeneous polynomial, in the projective case.)
Algebraic curves have been studied extensively since the 18th century.
Every algebraic plane curve has a degree, the degree of the defining equation, which is equal, in case of an algebraically closed field, to the number of intersections of the curve with a line in general position. For example, the circle given by the equation  has degree 2.
has degree 2.
The non-singular plane algebraic curves of degree 2 are called conic sections, and their projective completion are all isomorphic to the projective completion of the circle  (that is the projective curve of equation
(that is the projective curve of equation  ). The plane curves of degree 3 are called cubic plane curves and, if they are non-singular, elliptic curves. Those of degree 4 are called quartic plane curves.
). The plane curves of degree 3 are called cubic plane curves and, if they are non-singular, elliptic curves. Those of degree 4 are called quartic plane curves.
Examples
Numerous examples of plane curves are shown in Gallery of curves and listed at List of curves. The algebraic curves of degree 1 or 2 are shown here (an algebraic curve of degree less than 3 is always contained in a plane):
| Name
|
Implicit equation
|
Parametric equation
|
As a function
|
graph
|
| Straight line
|

|

|

|
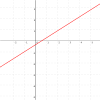
|
| Circle
|

|

|
|
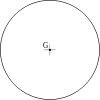
|
| Parabola
|

|

|

|
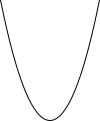
|
| Ellipse
|

|

|
|

|
| Hyperbola
|

|

|
|

|






























