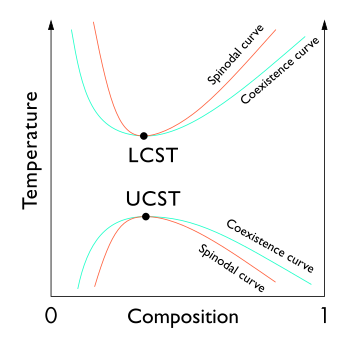
In thermodynamics, the limit of local stability with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero.
The locus of these points (the inflection point within a G-x or G-c curve, Gibbs free energy as a function of composition) is known as the spinodal curve.[1][2][3] For compositions within this curve, infinitesimally small fluctuations in composition and density will lead to phase separation via spinodal decomposition. Outside of the curve, the solution will be at least metastable with respect to fluctuations.[3] In other words, outside the spinodal curve some careful process may obtain a single phase system.[3] Inside it, only processes far from thermodynamic equilibrium, such as physical vapor deposition, will enable one to prepare single phase compositions.[4] The local points of coexisting compositions, defined by the common tangent construction, are known as a binodal coexistence curve, which denotes the minimum-energy equilibrium state of the system. Increasing temperature results in a decreasing difference between mixing entropy and mixing enthalpy, and thus the coexisting compositions come closer. The binodal curve forms the basis for the miscibility gap in a phase diagram. The free energy of mixing changes with temperature and concentration, and the binodal and spinodal meet at the critical or consolute temperature and composition.[5]