
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.

In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.
|
"Rigid graph" redirects here. For the meaning "has no nontrivial automorphisms", see Asymmetric graph. |
Rigidity is the property of a structure that it does not bend or flex under an applied force. The opposite of rigidity is flexibility. In structural rigidity theory, structures are formed by collections of objects that are themselves rigid bodies, often assumed to take simple geometric forms such as straight rods (line segments), with pairs of objects connected by flexible hinges. A structure is rigid if it cannot flex; that is, if there is no continuous motion of the structure that preserves the shape of its rigid components and the pattern of their connections at the hinges.
There are two essentially different kinds of rigidity. Finite or macroscopic rigidity means that the structure will not flex, fold, or bend by a positive amount. Infinitesimal rigidity means that the structure will not flex by even an amount that is too small to be detected even in theory. (Technically, that means certain differential equations have no nonzero solutions.) The importance of finite rigidity is obvious, but infinitesimal rigidity is also crucial because infinitesimal flexibility in theory corresponds to real-world minuscule flexing, and consequent deterioration of the structure.
A rigid graph is an embedding of a graph in a Euclidean space which is structurally rigid.[1] That is, a graph is rigid if the structure formed by replacing the edges by rigid rods and the vertices by flexible hinges is rigid. A graph that is not rigid is called flexible. More formally, a graph embedding is flexible if the vertices can be moved continuously, preserving the distances between adjacent vertices, with the result that the distances between some nonadjacent vertices are altered.[2] The latter condition rules out Euclidean congruences such as simple translation and rotation.
It is also possible to consider rigidity problems for graphs in which some edges represent compression elements (able to stretch to a longer length, but not to shrink to a shorter length) while other edges represent tension elements (able to shrink but not stretch). A rigid graph with edges of these types forms a mathematical model of a tensegrity structure.
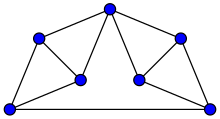
The fundamental problem is how to predict the rigidity of a structure by theoretical analysis, without having to build it. Key results in this area include the following:
However, in many other simple situations it is not yet always known how to analyze the rigidity of a structure mathematically despite the existence of considerable mathematical theory.
One of the founders of the mathematical theory of structural rigidity was the physicist James Clerk Maxwell. The late twentieth century saw an efflorescence of the mathematical theory of rigidity, which continues in the twenty-first century.
"[A] theory of the equilibrium and deflections of frameworks subjected to the action of forces is acting on the hardnes of quality... in cases in which the framework ... is strengthened by additional connecting pieces ... in cases of three dimensions, by the regular method of equations of forces, every point would have three equations to determine its equilibrium, so as to give 3s equations between e unknown quantities, if s be the number of points and e the number of connexions[sic]. There are, however, six equations of equilibrium of the system which must be fulfilled necessarily by the forces, on account of the equality of action and reaction in each piece. Hence if e = 3s − 6, the effect of any eternal force will be definite in producing tensions or pressures in the different pieces; but if e > 3s − 6, these forces will be indeterminate...."[5]