Types of transmitters
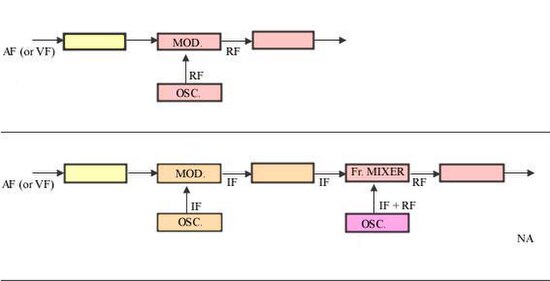
There are two types of transmitters. In some transmitters, the information signal (audio (AF), video (VF) etc.) modulates the radio frequency (RF) signal. These direct modulation transmitters are relatively simple transmitters.
In more complicated transmitters which are called superheterodyne, the information signal modulates an intermediate frequency (IF) signal. After stages for correction, equalization and sometimes amplification, the IF signal is converted to an RF signal by a stage named frequency mixer or frequency converter. Superheterodyne transmitters are more complex than direct modulation transmitters.[citation needed]











