| Truncated cuboctahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 26, E = 72, V = 48 (χ = 2) |
| Faces by sides | 12{4}+8{6}+6{8} |
| Conway notation | bC or taC |
| Schläfli symbols | tr{4,3} or |
| t0,1,2{4,3} | |
| Wythoff symbol | 2 3 4 | |
| Coxeter diagram | |
| Symmetry group | Oh, B3, [4,3], (*432), order 48 |
| Rotation group | O, [4,3]+, (432), order 24 |
| Dihedral angle | |
| References | U11, C23, W15 |
| Properties | Semiregular convex zonohedron |
 Colored faces |
 4.6.8 (Vertex figure) |
 Disdyakis dodecahedron (dual polyhedron) |
 Net |
In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
|
The name truncated cuboctahedron, given originally by Johannes Kepler, is misleading: an actual truncation of a cuboctahedron has rectangles instead of squares; however, this nonuniform polyhedron is topologically equivalent to the Archimedean solid unrigorously named truncated cuboctahedron. Alternate interchangeable names are:
|
There is a nonconvex uniform polyhedron with a similar name: the nonconvex great rhombicuboctahedron.
The Cartesian coordinates for the vertices of a truncated cuboctahedron having edge length 2 and centered at the origin are all the permutations of:
The area A and the volume V of the truncated cuboctahedron of edge length a are:
The truncated cuboctahedron is the convex hull of a rhombicuboctahedron with cubes above its 12 squares on 2-fold symmetry axes. The rest of its space can be dissected into 6 square cupolas below the octagons, and 8 triangular cupolas below the hexagons.
A dissected truncated cuboctahedron can create a genus 5, 7, or 11 Stewart toroid by removing the central rhombicuboctahedron, and either the 6 square cupolas, the 8 triangular cupolas, or the 12 cubes respectively. Many other lower symmetry toroids can also be constructed by removing the central rhombicuboctahedron, and a subset of the other dissection components. For example, removing 4 of the triangular cupolas creates a genus 3 toroid; if these cupolas are appropriately chosen, then this toroid has tetrahedral symmetry.[4][5]
| Stewart toroids | |||
|---|---|---|---|
| Genus 3 | Genus 5 | Genus 7 | Genus 11 |

|

|

|

|
There is only one uniform coloring of the faces of this polyhedron, one color for each face type.
A 2-uniform coloring, with tetrahedral symmetry, exists with alternately colored hexagons.
The truncated cuboctahedron has two special orthogonal projections in the A2 and B2 Coxeter planes with [6] and [8] projective symmetry, and numerous [2] symmetries can be constructed from various projected planes relative to the polyhedron elements.
The truncated cuboctahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

|

|
|

|
| Orthogonal projection | square-centered | hexagon-centered | octagon-centered |
|---|---|---|---|
| Stereographic projections | |||
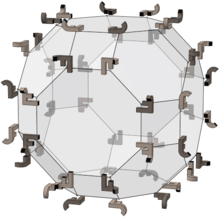
Like many other solids the truncated octahedron has full octahedral symmetry - but its relationship with the full octahedral group is closer than that: Its 48 vertices correspond to the elements of the group, and each face of its dual is a fundamental domain of the group.
The image on the right shows the 48 permutations in the group applied to an example object (namely the light JF compound on the left). The 24 light elements are rotations, and the dark ones are their reflections.
The edges of the solid correspond to the 9 reflections in the group:
The subgroups correspond to solids that share the respective vertices of the truncated octahedron.
E.g. the 3 subgroups with 24 elements correspond to a nonuniform snub cube with chiral octahedral symmetry, a nonuniform rhombicuboctahedron with pyritohedral symmetry (the cantic snub octahedron) and a nonuniform truncated octahedron with full tetrahedral symmetry. The unique subgroup with 12 elements is the alternating group A4. It corresponds to a nonuniform icosahedron with chiral tetrahedral symmetry.
| Subgroups and corresponding solids | ||||
|---|---|---|---|---|
| Truncated cuboctahedron tr{4,3} |
Snub cube sr{4,3} |
Rhombicuboctahedron s2{3,4} |
Truncated octahedron h1,2{4,3} |
Icosahedron |
| [4,3] Full octahedral |
[4,3]+ Chiral octahedral |
[4,3+] Pyritohedral |
[1+,4,3] = [3,3] Full tetrahedral |
[1+,4,3+] = [3,3]+ Chiral tetrahedral |

|

|

|

|

|
| all 48 vertices | 24 vertices | 12 vertices | ||

|

|
| Bowtie tetrahedron and cube contain two trapezoidal faces in place of each square.[6] | |
The truncated cuboctahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
This polyhedron can be considered a member of a sequence of uniform patterns with vertex configuration (4.6.2p) and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]() . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p < 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
. For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p < 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
| *n32 symmetry mutation of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures | 
|

|

|

|

|

|

|

|

|

|

| |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | 
|

|

|

|

|

|

|

|

|

|

|

|
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
| *n32 symmetry mutation of omnitruncated tilings: 6.8.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n43 [(n,4,3)] |
Spherical | Compact hyperbolic | Paraco. | |||||||||
| *243 [4,3] |
*343 [(3,4,3)] |
*443 [(4,4,3)] |
*543 [(5,4,3)] |
*643 [(6,4,3)] |
*743 [(7,4,3)] |
*843 [(8,4,3)] |
*∞43 [(∞,4,3)] | |||||
| Figures | 
|

|

|

|

|

|

|

| ||||
| Config. | 4.8.6 | 6.8.6 | 8.8.6 | 10.8.6 | 12.8.6 | 14.8.6 | 16.8.6 | ∞.8.6 | ||||
| Duals | 
|

|

|

|

|

|

|

| ||||
| Config. | V4.8.6 | V6.8.6 | V8.8.6 | V10.8.6 | V12.8.6 | V14.8.6 | V16.8.6 | V6.8.∞ | ||||
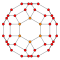
It is first in a series of cantitruncated hypercubes:
|
|
 
|
 
|
 
|
 
|
| Truncated cuboctahedron | Cantitruncated tesseract | Cantitruncated 5-cube | Cantitruncated 6-cube | Cantitruncated 7-cube | Cantitruncated 8-cube |
| Truncated cuboctahedral graph | |
|---|---|
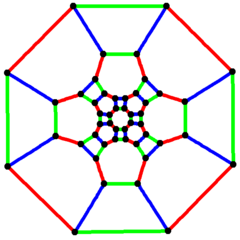 4-fold symmetry | |
| Vertices | 48 |
| Edges | 72 |
| Automorphisms | 48 |
| Chromatic number | 2 |
| Properties | Cubic, Hamiltonian, regular, zero-symmetric |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a truncated cuboctahedral graph (or great rhombcuboctahedral graph) is the graph of vertices and edges of the truncated cuboctahedron, one of the Archimedean solids. It has 48 vertices and 72 edges, and is a zero-symmetric and cubic Archimedean graph.[7]