


Centrifugal compressors, sometimes called impeller compressors or radial compressors, are a sub-class of dynamic axisymmetric work-absorbing turbomachinery.[1]
They achieve pressure rise by adding energy to the continuous flow of fluid through the rotor/impeller. The equation in the next section shows this specific energy input. A substantial portion of this energy is kinetic which is converted to increased potential energy/static pressure by slowing the flow through a diffuser. The static pressure rise in the impeller may roughly equal the rise in the diffuser.

A simple centrifugal compressor stage has four components (listed in order of throughflow): inlet, impeller/rotor, diffuser, and collector.[1] Figure 1.1 shows each of the components of the flow path, with the flow (working gas) entering the centrifugal impeller axially from left to right. This turboshaft (or turboprop) impeller is rotating counter-clockwise when looking downstream into the compressor. The flow will pass through the compressors from left to right.
The simplest inlet to a centrifugal compressor is typically a simple pipe. Depending upon its use/application inlets can be very complex. They may include other components such as an inlet throttle valve, a shrouded port, an annular duct (see Figure 1.1), a bifurcated duct, stationary guide vanes/airfoils used to straight or swirl flow (see Figure 1.1), movable guide vanes (used to vary pre-swirl adjustably). Compressor inlets often include instrumentation to measure pressure and temperature in order to control compressor performance.
Bernoulli's fluid dynamic principle plays an important role in understanding vaneless stationary components like an inlet. In engineering situations assuming adiabatic flow, this equation can be written in the form:
Equation-1.1
where:

The identifying component of a centrifugal compressor stage is the centrifugal impeller rotor. Impellers are designed in many configurations including "open" (visible blades), "covered or shrouded", "with splitters" (every other inducer removed), and "w/o splitters" (all full blades). Figures 0.1, 1.2.1, and 1.3 show three different open full inducer rotors with alternating full blades/vanes and shorter length splitter blades/vanes. Generally, the accepted mathematical nomenclature refers to the leading edge of the impeller with subscript 1. Correspondingly, the trailing edge of the impeller is referred to as subscript 2.
As working-gas/flow passes through the impeller from stations 1 to 2, the kinetic and potential energy increase. This is identical to an axial compressor with the exception that the gases can reach higher energy levels through the impeller's increasing radius. In many modern high-efficiency centrifugal compressors the gas exiting the impeller is traveling near the speed of sound.
Most modern high-efficiency impellers use "backsweep" in the blade shape.[2][3][4]
A derivation of the general Euler equations (fluid dynamics) is Euler's pump and turbine equation, which plays an important role in understanding impeller performance. This equation can be written in the form:
Equation-1.2 (see Figures 1.2.2 and 1.2.3 illustrating impeller velocity triangles)
where:

The next component, downstream of the impeller within a simple centrifugal compressor may the diffuser.[5][4] The diffuser converts the flow's kinetic energy (high velocity) into increased potential energy (static pressure) by gradually slowing (diffusing) the gas velocity. Diffusers can be vaneless, vaned, or an alternating combination. High-efficiency vaned diffusers are also designed over a wide range of solidities from less than 1 to over 4. Hybrid versions of vaned diffusers include wedge (see Figure 1.3), channel, and pipe diffusers. Some turbochargers have no diffuser. Generally accepted nomenclature might refer to the diffuser's lead edge as station 3 and the trailing edge as station 4.
Bernoulli's fluid dynamic principle plays an important role in understanding diffuser performance. In engineering situations assuming adiabatic flow, this equation can be written in the form:
Equation-1.3
where:

The collector of a centrifugal compressor can take many shapes and forms.[5][4] When the diffuser discharges into a large empty circumferentially (constant area) chamber, the collector may be termed a Plenum. When the diffuser discharges into a device that looks somewhat like a snail shell, bull's horn, or a French horn, the collector is likely to be termed a volute or scroll.
When the diffuser discharges into an annular bend the collector may be referred to as a combustor inlet (as used in jet engines or gas turbines) or a return-channel (as used in an online multi-stage compressor). As the name implies, a collector's purpose is to gather the flow from the diffuser discharge annulus and deliver this flow downstream into whatever component the application requires. The collector or discharge pipe may also contain valves and instrumentation to control the compressor. In some applications, collectors will diffuse flow (converting kinetic energy to static pressure) far less efficiently than a diffuser.[6]
Bernoulli's fluid dynamic principle plays an important role in understanding diffuser performance. In engineering situations assuming adiatice flow, this equation can be written in the form:
Equation-1.4
where:
Over the past 100 years, applied scientists including Stodola (1903, 1927–1945),[7] Pfleiderer (1952),[8] Hawthorne (1964),[9] Shepherd (1956),[1] Lakshminarayana (1996),[10] and Japikse (many texts including citations),[2][11][citation needed][12] have educated young engineers in the fundamentals of turbomachinery. These understandings apply to all dynamic, continuous-flow, axisymmetric pumps, fans, blowers, and compressors in axial, mixed-flow and radial/centrifugal configurations.
This relationship is the reason advances in turbines and axial compressors often find their way into other turbomachinery including centrifugal compressors. Figures 2.1 and 2.2 illustrate the domain of turbomachinery with labels showing centrifugal compressors.[13][14] Improvements in centrifugal compressors have not been achieved through large discoveries. Rather, improvements have been achieved through understanding and applying incremental pieces of knowledge discovered by many individuals.

Figure 2.1 (shown right) represents the aero-thermo domain of turbomachinery. The horizontal axis represents the energy equation derivable from The first law of thermodynamics.[1][14] The vertical axis, which can be characterized by Mach Number, represents the range of fluid compressibility (or elasticity).[1][14] The Z-axis, which can be characterized by Reynolds number, represents the range of fluid viscosities (or stickiness).[14] Mathematicians and physicists who established the foundations of this aero-thermo domain include:[15][16] Isaac Newton, Daniel Bernoulli, Leonhard Euler, Claude-Louis Navier, George Stokes, Ernst Mach, Nikolay Yegorovich Zhukovsky, Martin Kutta, Ludwig Prandtl, Theodore von Kármán, Paul Richard Heinrich Blasius, and Henri Coandă.

Figure 2.2 (shown right) represents the physical or mechanical domain of turbomachinery. Again, the horizontal axis represents the energy equation with turbines generating power to the left and compressors absorbing power to the right.[1][14] Within the physical domain the vertical axis differentiates between high speeds and low speeds depending upon the turbomachinery application.[1][14] The Z-axis differentiates between axial-flow geometry and radial-flow geometry within the physical domain of turbomachinery.[1][14] It is implied that mixed-flow turbomachinery lie between axial and radial.[1][14] Key contributors of technical achievements that pushed the practical application of turbomachinery forward include:[15][16] Denis Papin,[17] Kernelien Le Demour, Daniel Gabriel Fahrenheit, John Smeaton, Dr. A. C. E. Rateau,[18] John Barber, Alexander Sablukov, Sir Charles Algernon Parsons, Ægidius Elling, Sanford Alexander Moss, Willis Carrier, Adolf Busemann, Hermann Schlichting, Frank Whittle and Hans von Ohain.
| <1689 | Early turbomachines | Pumps, blowers, fans |
| 1689 | Denis Papin | Origin of the centrifugal compressor |
| 1754 | Leonhard Euler | Euler's "Pump & Turbine" equation |
| 1791 | John Barber | First gas turbine patent |
| 1899 | A. C. E. Rateau | First practical centrifugal compressor |
| 1927 | Aurel Boleslav Stodola | Formalized "slip factor" |
| 1928 | Adolf Busemann | Derived "slip factor" |
| 1937 | Frank Whittle and Hans von Ohain, independently | First gas turbine using a centrifugal compressor |
| >1970 | Modern turbomachines | 3D-CFD, rocket turbo-pumps, heart assist pumps, turbocharged fuel cells |
Centrifugal compressors are similar in many ways to other turbomachinery and are compared and contrasted as follows:

Centrifugal compressors are similar to axial compressors in that they are rotating airfoil-based compressors. Both are shown in the adjacent photograph of an engine with 5 stages of axial compressors and one stage of a centrifugal compressor.[10] The first part of the centrifugal impeller looks very similar to an axial compressor. This first part of the centrifugal impeller is also termed an inducer. Centrifugal compressors differ from axials as they use a significant change in radius from inlet to exit of the impeller to produce a much greater pressure rise in a single stage (e.g. 8[19] in the Pratt & Whitney Canada PW200 series of helicopter engines) than does an axial stage. The 1940s-era German Heinkel HeS 011 experimental engine was the first aviation turbojet to have a compressor stage with radial flow-turning part-way between none for an axial and 90 degrees for a centrifugal. It is known as a mixed/diagonal-flow compressor. A diagonal stage is used in the Pratt & Whitney Canada PW600 series of small turbofans.

Centrifugal compressors are also similar to centrifugal fans of the style shown in the neighboring figure as they both increase the energy of the flow through the increasing radius.[1] In contrast to centrifugal fans, compressors operate at higher speeds to generate greater pressure rises. In many cases, the engineering methods used to design a centrifugal fan are the same as those to design a centrifugal compressor, so they can look very similar.
For purposes of generalization and definition, it can be said that centrifugal compressors often have density increases greater than 5 percent. Also, they often experience relative fluid velocities above Mach number 0.3[20] when the working fluid is air or nitrogen. In contrast, fans or blowers are often considered to have density increases of less than five percent and peak relative fluid velocities below Mach 0.3.

Squirrel-cage fans are primarily used for ventilation. The flow field within this type of fan has internal recirculations. In comparison, a centrifugal fan is uniform circumferentially.
Centrifugal compressors are also similar to centrifugal pumps[1] of the style shown in the adjacent figures. The key difference between such compressors and pumps is that the compressor working fluid is a gas (compressible) and the pump working fluid is liquid (incompressible). Again, the engineering methods used to design a centrifugal pump are the same as those to design a centrifugal compressor. Yet, there is one important difference: the need to deal with cavitation in pumps.
Centrifugal compressors also look very similar to their turbomachinery counterpart the radial turbine as shown in the figure. While a compressor transfers energy into a flow to raise its pressure, a turbine operates in reverse, by extracting energy from a flow, thus reducing its pressure.[citation needed] In other words, power is input to compressors and output from turbines.
As turbomachinery became more common, standards have been created to guide manufacturers to assure end-users that their products meet minimum safety and performance requirements. Associations formed to codify these standards rely on manufacturers, end-users, and related technical specialists. A partial list of these associations and their standards are listed below:
Below, is a partial list of centrifugal compressor applications each with a brief description of some of the general characteristics possessed by those compressors. To start this list two of the most well-known centrifugal compressor applications are listed; gas turbines and turbochargers.[10]


In the case where flow passes through a straight pipe to enter a centrifugal compressor, the flow is axial, uniform, and has no vorticity, i.e. swirling motion. As the flow passes through the centrifugal impeller, the impeller forces the flow to spin faster as it gets further from the rotational axis. According to a form of Euler's fluid dynamics equation, known as the pump and turbine equation, the energy input to the fluid is proportional to the flow's local spinning velocity multiplied by the local impeller tangential velocity.
In many cases, the flow leaving the centrifugal impeller is traveling near the speed of sound. It then flows through a stationary compressor causing it to decelerate. The stationary compressor is ducting with increasing flow-area where energy transformation takes place. If the flow has to be turned in a rearward direction to enter the next part of the machine, e.g. another impeller or a combustor, flow losses can be reduced by directing the flow with stationary turning vanes or individual turning pipes (pipe diffusers). As described in Bernoulli's principle, the reduction in velocity causes the pressure to rise.[1]

While illustrating a gas turbine's Brayton cycle,[15] Figure 5.1 includes example plots of pressure-specific volume and temperature-entropy. These types of plots are fundamental to understanding centrifugal compressor performance at one operating point. The two plots show that the pressure rises between the compressor inlet (station 1) and compressor exit (station 2). At the same time, the specific volume decreases while the density increases. The temperature-entropy plot shows that the temperature increases with increasing entropy (loss). Assuming dry air, and the ideal gas equation of state and an isentropic process, there is enough information to define the pressure ratio and efficiency for this one point. The compressor map is required to understand the compressor performance over its complete operating range.
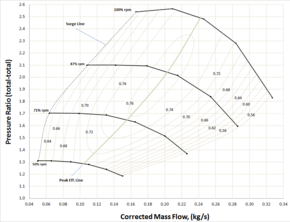
Figure 5.2, a centrifugal compressor performance map (either test or estimated), shows the flow, pressure ratio for each of 4 speed-lines (total of 23 data points). Also included are constant efficiency contours. Centrifugal compressor performance presented in this form provides enough information to match the hardware represented by the map to a simple set of end-user requirements.
Compared to estimating performance which is very cost effective (thus useful in design), testing, while costly, is still the most precise method.[12] Further, testing centrifugal compressor performance is very complex. Professional societies such as ASME (i.e. PTC–10, Fluid Meters Handbook, PTC-19.x),[34] ASHRAE (ASHRAE Handbook) and API (ANSI/API 617–2002, 672–2007)[31][33] have established standards for detailed experimental methods and analysis of test results. Despite this complexity, a few basic concepts in performance can be presented by examining an example test performance map.
Pressure ratio and flow are the main parameters[15][31][33][34] needed to match the Figure 5.2 performance map to a simple compressor application. In this case, it can be assumed that the inlet temperature is sea-level standard. This assumption is not acceptable in practice as inlet temperature variations cause significant variations in compressor performance. Figure 5.2 shows:
As is standard practice, Figure 5.2 has a horizontal axis labeled with a flow parameter. While flow measurements use a variety of units, all fit one of 2 categories:
Mass flow units, such as kg/s, are the easiest to use in practice as there is little room for confusion. Questions remaining would involve inlet or outlet (which might involve leakage from the compressor or moisture condensation). For atmospheric air, the mass flow may be wet or dry (including or excluding humidity). Often, the mass flow specification will be presented on an equivalent Mach number basis, .[35] It is standard in these cases that the equivalent temperature, equivalent pressure, and gas is specified explicitly or implied at a standard condition.
In contrast, all volume flow specifications require the additional specification of density. Bernoulli's fluid dynamic principle is of great value in understanding this problem. Confusion arises through either inaccuracies or misuse of pressure, temperature, and gas constants.
Also as is standard practice, Figure 5.2 has a vertical axis labeled with a pressure parameter. There is a variety of pressure measurement units. They all fit one of two categories:
The pressure rise may alternatively be specified as a ratio that has no units:
Other features common to performance maps are:
The two most common methods for producing a map for a centrifugal compressor are at constant shaft speed or with a constant throttle setting. If the speed is held constant, test points are taken along a constant speed line by changing throttle positions. In contrast, if a throttle valve is held constant, test points are established by changing speed and repeated with different throttle positions (common gas turbine practice). The map shown in Figure 5.2 illustrates the most common method; lines of constant speed. In this case, we see data points connected via straight lines at speeds of 50%, 71%, 87%, and 100% RPM. The first three speed-lines have 6 points each while the highest speed line has five.
The next feature to be discussed is the oval-shaped curves representing islands of constant efficiency. In this figure we see 11 contours ranging from 56% efficiency (decimal 0.56) to 76% efficiency (decimal 0.76). General standard practice is to interpret these efficiencies as isentropic rather than polytropic. The inclusion of efficiency islands effectively generates a 3-dimensional topology to this 2-dimensional map. With inlet density specified, it provides a further ability to calculate aerodynamic power. Lines of constant power could just as easily be substituted.
Regarding gas turbine operation and performance, there may be a series of guaranteed points established for the gas turbine's centrifugal compressor. These requirements are of secondary importance to the overall gas turbine performance as a whole. For this reason, it is only necessary to summarize that in the ideal case, the lowest specific fuel consumption would occur when the centrifugal compressor's peak efficiency curve coincides with the gas turbine's required operation line.
In contrast to gas turbines, most other applications (including industrial) need to meet a less stringent set of performance requirements. Historically, centrifugal compressors applied to industrial applications were needed to achieve performance at a specific flow and pressure. Modern industrial compressors are often needed to achieve specific performance goals across a range of flows and pressures; thus taking a significant step toward the sophistication seen in gas turbine applications.
If the compressor represented in Figure 5.2 is used in a simple application, any point (pressure and flow) within the 76% efficiency would provide very acceptable performance. An "End User" would be very happy with the performance requirements of 2.0 pressure ratio at 0.21 kg/s.
Surge - is a low flow phenomenon where the impeller cannot add enough energy to overcome the system resistance or backpressure.[36] At low flow rate operation, the pressure ratio over the impeller is high, as is back system backpressure. Under critical conditions, the flow will reverse back over the tips of the rotor blades towards the impeller eye (inlet).[37] This stalling flow reversal may go unnoticed as the fraction of mass flow or energy is too low. When large enough, rapid flow reversal occurs(i.e., surge). The reversed flow exiting the impeller inlet exhibits a strong rotational component, which affects lower radius flow angles (closer to the impeller hub) at the leading edge of the blades. The deterioration of the flow angles causes the impeller to be inefficient. A full flow reversal can occur. (Therefore, surge is sometimes referred to as axisymmetric stall.) When reversed flow reduces to a low enough level, the impeller recovers and regains stability for a short moment at which point the stage may surge again. These cyclic events cause large vibrations, increase temperature and change rapidly the axial thrust. These occurrences can damage the rotor seals, rotor bearings, the compressor driver, and cycle operation. Most turbomachines are designed to easily withstand occasional surging. However, if the machine is forced to surge repeatedly for a long period of time, or if it is poorly designed, repeated surges can result in a catastrophic failure. Of particular interest, is that while turbomachines may be very durable, their physical system can be far less robust.

The surge-line shown in Figure 5.2 is the curve that passes through the lowest flow points of each of the four speed-lines. As a test map, these points would be the lowest flow points possible to record a stable reading within the test facility/rig. In many industrial applications, it may be necessary to increase the stall line due to the system backpressure. For example, at 100% RPM stalling flow might increase from approximately 0.170 kg/s to 0.215 kg/s because of the positive slope of the pressure ratio curve.
As stated earlier, the reason for this is that the high-speed line in Figure 5.2 exhibits a stalling characteristic or positive slope within that range of flows. When placed in a different system those lower flows might not be achievable because of interaction with that system. System resistance or adverse pressure is proven mathematically to be the critical contributor to compressor surge.
Choke occurs under one of 2 conditions. Typically for high speed equipment, as flow increases the velocity of the flow can approach sonic speed somewhere within the compressor stage. This location may occur at the impeller inlet "throat" or at the vaned diffuser inlet "throat". In contrast, for lower speed equipment, as flows increase, losses increase such that the pressure ratio eventually drops to 1:1. In this case, the occurrence of choke is unlikely.
The speed-lines of gas turbine centrifugal compressors typically exhibit choke. This is a situation where the pressure ratio of a speed line drops rapidly (vertically) with little or no change in flow. In most cases the reason for this is that close to Mach 1 velocities have been reached somewhere within the impeller and/or diffuser generating a rapid increase in losses. Higher pressure ratio turbocharger centrifugal compressors exhibit this same phenomenon. Real choke phenomena is a function of compressibility as measured by the local Mach number within an area restriction within the centrifugal pressure stage.
The maximum flow line, shown in Figure 5.2, is the curve that passes through the highest flow points of each speed line. Upon inspection it may be noticed that each of these points has been taken near 56% efficiency. Selecting a low efficiency (<60%) is the most common practice used to terminate compressor performance maps at high flows. Another factor that is used to establish the maximum flow line is a pressure ratio near or equal to 1. The 50% speed line may be considered an example of this.
The shape of Figure 5.2's speed-lines provides a good example of why it is inappropriate to use the term choke in association with a maximum flow of all centrifugal compressor speed-lines. In summary; most industrial and commercial centrifugal compressors are selected or designed to operate at or near their highest efficiencies and to avoid operation at low efficiencies. For this reason there is seldom a reason to illustrate centrifugal compressor performance below 60% efficiency.
Many industrial and commercial multistage compressor performance maps exhibits this same vertical characteristic for a different reason related to what is known as stage stacking.
To weigh the advantages between centrifugal compressors it is important to compare 8 parameters classic to turbomachinery. Specifically, pressure rise (p), flow (Q), angular speed (N), power (P), density (ρ), diameter (D), viscosity (μ) and elasticity (e). This creates a practical problem when trying to experimentally determine the effect of any one parameter. This is because it is nearly impossible to change one of these parameters independently.
The method of procedure known as the Buckingham π theorem can help solve this problem by generating 5 dimensionless forms of these parameters.[1][citation needed][16] These Pi parameters provide the foundation for "similitude" and the "affinity-laws" in turbomachinery. They provide for the creation of additional relationships (being dimensionless) found valuable in the characterization of performance.
For the example below Head will be substituted for pressure and sonic velocity will be substituted for elasticity.
|
Main article: Buckingham π theorem |
The three independent dimensions used in this procedure for turbomachinery are:
According to the theorem each of the eight main parameters are equated to its independent dimensions as follows:
| Flow | ex. = m3/s | ||
| Head | ex. = kg·m/s2 | ||
| Speed | ex. = m/s | ||
| Power | ex. = kg·m2/s3 | ||
| Density | ex. = kg/m3 | ||
| Viscosity | ex. = kg/m·s | ||
| Diameter | ex. = m | ||
| Speed of sound | ex. = m/s |
Completing the task of following the formal procedure results in generating this classic set of five dimensionless parameters for turbomachinery.[1] Full-similitude is achieved when each one of the 5 Pi-parameters is equivalent when comparing two different cases. This of course would mean the two turbomachines being compared are similar, both geometrically and in terms of performance.
| 1 | Flow-coefficient | ||
| Head-coefficient | |||
| 3 | Speed-coefficient | ||
| 4 | Power-coefficient | ||
| 5 | Reynolds-coefficient |
Turbomachinery analysts gain tremendous insight into performance by comparisons of the 5 parameters shown in the above table. Particularly, performance parameters such as efficiencies and loss-coefficients, which are also dimensionless. In general application, the Flow-coefficient and Head-coefficient are considered of primary importance. Generally, for centrifugal compressors, the Speed-coefficient is of secondary importance while the Reynolds-coefficient is of tertiary importance. In contrast, as expected for pumps, the Reynolds-coefficient becomes of secondary importance and the Speed-coefficient of tertiary importance. It may be found interesting that the Speed-coefficient may be chosen to define the y-axis of Figure 1.1, while at the same time the Reynolds coefficient may be chosen to define the z-axis.
Demonstrated in the table below is another value of dimensional analysis. Any number of new dimensionless parameters can be calculated through exponents and multiplication. For example, a variation of the first parameter shown below is popularly used in aircraft engine system analysis. The third parameter is a simplified dimensional variation of the first and second. This third definition is applicable with strict limitations. The fourth parameter, specific speed, is very well known and useful in that it removes diameter. The fifth parameter, specific diameter, is a less often discussed dimensionless parameter found useful by Balje.[38]
| 1 | Corrected mass flow coefficient | ||
| 2 | Alternate#1 equivalent Mach form | ||
| 3 | Alternate#2 simplified dimensional form | ||
| 4 | Specific speed coefficient | ||
| 5 | Specific diameter coefficient |
It may be found interesting that the specific speed coefficient may be used in place of speed to define the y-axis of Figure 1.2, while at the same time, the specific diameter coefficient may be in place of diameter to define the z-axis.
The following affinity laws are derived from the five Π-parameters shown above. They provide a simple basis for scaling turbomachinery from one application to the next.
| From flow coefficient | |||
| From head coefficient | |||
| From power coefficient |
The following equations outline a fully three-dimensional mathematical problem that is very difficult to solve even with simplifying assumptions.[10][39] Until recently, limitations in computational power, forced these equations to be simplified to an inviscid two-dimensional problem with pseudo losses. Before the advent of computers, these equations were almost always simplified to a one-dimensional problem.
Solving this one-dimensional problem is still valuable today and is often termed mean-line analysis. Even with all of this simplification it still requires large textbooks to outline and large computer programs to solve practically.
Also termed continuity, this fundamental equation written in general form is as follows:
Also termed the Navier–Stokes equations, this fundamental is derivable from Newton's second law when applied to fluid motion. Written in compressible form for a Newtonian fluid, this equation may be written as follows:
The first law of thermodynamics is the statement of the conservation of energy. Under specific conditions, the operation of a Centrifugal compressor is considered a reversible process. For a reversible process, the total amount of heat added to a system can be expressed as where is temperature and is entropy. Therefore, for a reversible process:
Since U, S and V are thermodynamic functions of state, the above relation holds also for non-reversible changes. The above equation is known as the fundamental thermodynamic relation.
The classical ideal gas law may be written:
The ideal gas law may also be expressed as follows
where is the density, is the adiabatic index (ratio of specific heats), is the internal energy per unit mass (the "specific internal energy"), is the specific heat at constant volume, and is the specific heat at constant pressure.
With regard to the equation of state, it is important to remember that while air and nitrogen properties (near standard atmospheric conditions) are easily and accurately estimated by this simple relationship, there are many centrifugal compressor applications where the ideal relationship is inadequate. For example, centrifugal compressors used for large air conditioning systems (water chillers) use a refrigerant as a working gas that cannot be modeled as an ideal gas. Another example are centrifugal compressors design and built for the petroleum industry. Most of the hydrocarbon gases such as methane and ethylene are best modeled as a real gas equation of state rather than ideal gases. The Wikipedia entry for equations of state is very thorough.
Ideally, centrifugal compressor impellers have thin air-foil blades that are strong, each mounted on a light rotor. This material would be easy to machine or cast and inexpensive. Additionally, it would generate no operating noise, and have a long life while operating in any environment.[clarification needed]
From the very start of the aero-thermodynamic design process, the aerodynamic considerations and optimizations [29,30] are critical to have a successful design. during the design, the centrifugal impeller's material and manufacturing method must be accounted for within the design, whether it be plastic for a vacuum cleaner blower, aluminum alloy for a turbocharger, steel alloy for an air compressor or titanium alloy for a gas turbine. It is a combination of the centrifugal compressor impeller shape, its operating environment, its material and its manufacturing method that determines the impeller's structural integrity.[40][41]