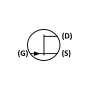
Electronic amplifier circuit type
In electronics, a common-drain amplifier, also known as a source follower, is one of three basic single-stage field-effect transistor (FET) amplifier topologies, typically used as a voltage buffer. In this circuit (NMOS) the gate terminal of the transistor serves as the signal input, the source is the output, and the drain is common to both (input and output), hence its name. Because of its low dependence on the load resistor on the voltage gain, it can be used to drive low resistance loads, such as a speaker. The analogous bipolar junction transistor circuit is the common-collector amplifier. This circuit is also commonly called a "stabilizer".
In addition, this circuit is used to transform impedances. For example, the Thévenin resistance of a combination of a voltage follower driven by a voltage source with high Thévenin resistance is reduced to only the output resistance of the voltage follower (a small resistance). That resistance reduction makes the combination a more ideal voltage source. Conversely, a voltage follower inserted between a driving stage and a high load (i.e. a low resistance) presents an infinite resistance (low load) to the driving stage—an advantage in coupling a voltage signal to a large load.