| Mathematical analysis → Complex analysis |
| Complex analysis |
|---|
 |
| Complex numbers |
| Complex functions |
| Basic theory |
| Geometric function theory |
| People |
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space Cn. The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (is analytic). Holomorphic functions are the central objects of study in complex analysis.
Though the term analytic function is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis.[1]
Holomorphic functions are also sometimes referred to as regular functions.[2] A holomorphic function whose domain is the whole complex plane is called an entire function. The phrase "holomorphic at a point z0" means not just differentiable at z0, but differentiable everywhere within some neighbourhood of z0 in the complex plane.
Definition
[edit]
Given a complex-valued function f of a single complex variable, the derivative of f at a point z0 in its domain is defined as the limit[3]
This is the same definition as for the derivative of a real function, except that all quantities are complex. In particular, the limit is taken as the complex number z tends to z0, and this means that the same value is obtained for any sequence of complex values for z that tends to z0. If the limit exists, f is said to be complex differentiable at z0. This concept of complex differentiability shares several properties with real differentiability: it is linear and obeys the product rule, quotient rule, and chain rule.[4]
A function is holomorphic on an open set U if it is complex differentiable at every point of U. A function f is holomorphic at a point z0 if it is holomorphic on some neighbourhood of z0.[5] A function is holomorphic on some non-open set A if it is holomorphic at every point of A.
A function may be complex differentiable at a point but not holomorphic at this point. For example, the function is complex differentiable at 0, but not complex differentiable elsewhere (see the Cauchy–Riemann equations, below). So, it is not holomorphic at 0.
The relationship between real differentiability and complex differentiability is the following: If a complex function f(x + i y) = u(x, y) + i v(x, y) is holomorphic, then u and v have first partial derivatives with respect to x and y, and satisfy the Cauchy–Riemann equations:[6]
or, equivalently, the Wirtinger derivative of f with respect to the complex conjugate of is zero:[7]
which is to say that, roughly, f is functionally independent from the complex conjugate of z.
If continuity is not given, the converse is not necessarily true. A simple converse is that if u and v have continuous first partial derivatives and satisfy the Cauchy–Riemann equations, then f is holomorphic. A more satisfying converse, which is much harder to prove, is the Looman–Menchoff theorem: if f is continuous, u and v have first partial derivatives (but not necessarily continuous), and they satisfy the Cauchy–Riemann equations, then f is holomorphic.[8]
Terminology
[edit]The term holomorphic was introduced in 1875 by Charles Briot and Jean-Claude Bouquet, two of Augustin-Louis Cauchy's students, and derives from the Greek ὅλος (hólos) meaning "whole", and μορφή (morphḗ) meaning "form" or "appearance" or "type", in contrast to the term meromorphic derived from μέρος (méros) meaning "part". A holomorphic function resembles an entire function ("whole") in a domain of the complex plane while a meromorphic function (defined to mean holomorphic except at certain isolated poles), resembles a rational fraction ("part") of entire functions in a domain of the complex plane.[9] Cauchy had instead used the term synectic.[10]
Today, the term "holomorphic function" is sometimes preferred to "analytic function". An important result in complex analysis is that every holomorphic function is complex analytic, a fact that does not follow obviously from the definitions. The term "analytic" is however also in wide use.
Properties
[edit]Because complex differentiation is linear and obeys the product, quotient, and chain rules, the sums, products and compositions of holomorphic functions are holomorphic, and the quotient of two holomorphic functions is holomorphic wherever the denominator is not zero.[11] That is, if functions f and g are holomorphic in a domain U, then so are f + g, f − g, f g, and f ∘ g. Furthermore, f / g is holomorphic if g has no zeros in U, or is meromorphic otherwise.
If one identifies C with the real plane R2, then the holomorphic functions coincide with those functions of two real variables with continuous first derivatives which solve the Cauchy–Riemann equations, a set of two partial differential equations.[6]
Every holomorphic function can be separated into its real and imaginary parts f(x + i y) = u(x, y) + i v(x, y), and each of these is a harmonic function on R2 (each satisfies Laplace's equation ∇2 u = ∇2 v = 0), with v the harmonic conjugate of u.[12] Conversely, every harmonic function u(x, y) on a simply connected domain Ω ⊂ R2 is the real part of a holomorphic function: If v is the harmonic conjugate of u, unique up to a constant, then f(x + i y) = u(x, y) + i v(x, y) is holomorphic.
Cauchy's integral theorem implies that the contour integral of every holomorphic function along a loop vanishes:[13]
Here γ is a rectifiable path in a simply connected complex domain U ⊂ C whose start point is equal to its end point, and f : U → C is a holomorphic function.
Cauchy's integral formula states that every function holomorphic inside a disk is completely determined by its values on the disk's boundary.[13] Furthermore: Suppose U ⊂ C is a complex domain, f : U → C is a holomorphic function and the closed disk D = {z : |z − z0| ≤ r} is completely contained in U. Let γ be the circle forming the boundary of D. Then for every a in the interior of D:
where the contour integral is taken counter-clockwise.
The derivative f′(a) can be written as a contour integral[13] using Cauchy's differentiation formula:
for any simple loop positively winding once around a, and
for infinitesimal positive loops γ around a.
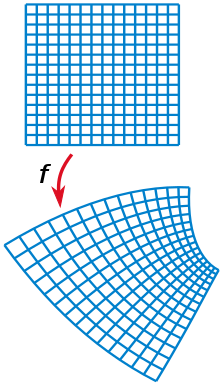
In regions where the first derivative is not zero, holomorphic functions are conformal: they preserve angles and the shape (but not size) of small figures.[14]
Every holomorphic function is analytic. That is, a holomorphic function f has derivatives of every order at each point a in its domain, and it coincides with its own Taylor series at a in a neighbourhood of a. In fact, f coincides with its Taylor series at a in any disk centred at that point and lying within the domain of the function.
From an algebraic point of view, the set of holomorphic functions on an open set is a commutative ring and a complex vector space. Additionally, the set of holomorphic functions in an open set U is an integral domain if and only if the open set U is connected. [7] In fact, it is a locally convex topological vector space, with the seminorms being the suprema on compact subsets.
From a geometric perspective, a function f is holomorphic at z0 if and only if its exterior derivative df in a neighbourhood U of z0 is equal to f′(z) dz for some continuous function f′. It follows from
that df′ is also proportional to dz, implying that the derivative f′ is itself holomorphic and thus that f is infinitely differentiable. Similarly, d(f dz) = f′ dz ∧ dz = 0 implies that any function f that is holomorphic on the simply connected region U is also integrable on U.
(For a path γ from z0 to z lying entirely in U, define in light of the Jordan curve theorem and the generalized Stokes' theorem, Fγ(z) is independent of the particular choice of path γ, and thus F(z) is a well-defined function on U having F(z0) = F0 and dF = f dz.)
Examples
[edit]All polynomial functions in z with complex coefficients are entire functions (holomorphic in the whole complex plane C), and so are the exponential function exp z and the trigonometric functions and (cf. Euler's formula). The principal branch of the complex logarithm function log z is holomorphic on the domain C ∖ {z ∈ R : z ≤ 0}. The square root function can be defined as and is therefore holomorphic wherever the logarithm log z is. The reciprocal function 1 / z is holomorphic on C ∖ {0}. (The reciprocal function, and any other rational function, is meromorphic on C.)
As a consequence of the Cauchy–Riemann equations, any real-valued holomorphic function must be constant. Therefore, the absolute value |z |, the argument arg (z), the real part Re (z) and the imaginary part Im (z) are not holomorphic. Another typical example of a continuous function which is not holomorphic is the complex conjugate (The complex conjugate is antiholomorphic.)
Several variables
[edit]The definition of a holomorphic function generalizes to several complex variables in a straightforward way. A function in n complex variables is analytic at a point p if there exists a neighbourhood of p in which f is equal to a convergent power series in n complex variables;[15] the function f is holomorphic in an open subset U of Cn if it is analytic at each point in U. Osgood's lemma shows (using the multivariate Cauchy integral formula) that, for a continuous function f, this is equivalent to f being holomorphic in each variable separately (meaning that if any n − 1 coordinates are fixed, then the restriction of f is a holomorphic function of the remaining coordinate). The much deeper Hartogs' theorem proves that the continuity assumption is unnecessary: f is holomorphic if and only if it is holomorphic in each variable separately.
More generally, a function of several complex variables that is square integrable over every compact subset of its domain is analytic if and only if it satisfies the Cauchy–Riemann equations in the sense of distributions.
Functions of several complex variables are in some basic ways more complicated than functions of a single complex variable. For example, the region of convergence of a power series is not necessarily an open ball; these regions are logarithmically-convex Reinhardt domains, the simplest example of which is a polydisk. However, they also come with some fundamental restrictions. Unlike functions of a single complex variable, the possible domains on which there are holomorphic functions that cannot be extended to larger domains are highly limited. Such a set is called a domain of holomorphy.
A complex differential (p, 0)-form α is holomorphic if and only if its antiholomorphic Dolbeault derivative is zero: ∂α = 0.
Extension to functional analysis
[edit]The concept of a holomorphic function can be extended to the infinite-dimensional spaces of functional analysis. For instance, the Fréchet or Gateaux derivative can be used to define a notion of a holomorphic function on a Banach space over the field of complex numbers.
See also
[edit]- Antiderivative (complex analysis)
- Antiholomorphic function
- Biholomorphy
- Holomorphic separability
- Meromorphic function
- Quadrature domains
- Harmonic maps
- Harmonic morphisms
- Wirtinger derivatives
References
[edit]- ^ Analytic functions of one complex variable, Encyclopedia of Mathematics. (European Mathematical Society ft. Springer, 2015)
- ^ "Analytic function", Encyclopedia of Mathematics, EMS Press, 2001 [1994], retrieved February 26, 2021
- ^ Ahlfors, L., Complex Analysis, 3 ed. (McGraw-Hill, 1979).
- ^ Henrici, P., Applied and Computational Complex Analysis (Wiley). [Three volumes: 1974, 1977, 1986.]
- ^ Peter Ebenfelt, Norbert Hungerbühler, Joseph J. Kohn, Ngaiming Mok, Emil J. Straube (2011) Complex Analysis Springer Science & Business Media
- ^ a b Markushevich, A.I.,Theory of Functions of a Complex Variable (Prentice-Hall, 1965). [Three volumes.]
- ^ a b Gunning, Robert C.; Rossi, Hugo (1965). Analytic Functions of Several Complex Variables. Prentice-Hall series in Modern Analysis. Englewood Cliffs, N.J.: Prentice-Hall. pp. xiv+317. ISBN 9780821869536. MR 0180696. Zbl 0141.08601.
- ^ Gray, J. D.; Morris, S. A. (1978), "When is a Function that Satisfies the Cauchy-Riemann Equations Analytic?", The American Mathematical Monthly, 85 (4) (published April 1978): 246–256, doi:10.2307/2321164, JSTOR 2321164.
- ^ The original French terms were holomorphe and méromorphe.
Briot, Charles Auguste; Bouquet, Jean-Claude (1875). "§15 fonctions holomorphes". Théorie des fonctions elliptiques (2nd ed.). Gauthier-Villars. pp. 14–15.
Lorsqu'une fonction est continue, monotrope, et a une dérivée, quand la variable se meut dans une certaine partie du plan, nous dirons qu'elle est holomorphe dans cette partie du plan. Nous indiquons par cette dénomination qu'elle est semblable aux fonctions entières qui jouissent de ces propriétés dans toute l'étendue du plan. [...] ¶ Une fraction rationnelle admet comme pôles les racines du dénominateur; c'est une fonction holomorphe dans toute partie du plan qui ne contient aucun de ses pôles. ¶ Lorsqu'une fonction est holomorphe dans une partie du plan, excepté en certains pôles, nous dirons qu'elle est méromorphe dans cette partie du plan, c'est-à-dire semblable aux fractions rationnelles.
[When a function is continuous, monotropic, and has a derivative, when the variable moves in a certain part of the plane, we say that it is holomorphic in that part of the plane. We mean by this name that it resembles entire functions which enjoy these properties in the full extent of the plane. [...] ¶ A rational fraction admits as poles the roots of the denominator; it is a holomorphic function in all that part of the plane which does not contain any poles. ¶ When a function is holomorphic in part of the plane, except at certain poles, we say that it is meromorphic in that part of the plane, that is to say it resembles rational fractions.]
Harkness, James; Morley, Frank (1893). "5. Integration". A Treatise on the Theory of Functions. Macmillan. p. 161. - ^ Briot & Bouquet had previously also adopted Cauchy’s term synectic (synectique in French), in the 1859 first edition of their book. Briot, Charles Auguste; Bouquet, Jean-Claude (1859). "§10". Théorie des fonctions doublement périodiques. Mallet-Bachelier. p. 11.
- ^ Henrici, Peter (1993) [1986], Applied and Computational Complex Analysis Volume 3, Wiley Classics Library (Reprint ed.), New York - Chichester - Brisbane - Toronto - Singapore: John Wiley & Sons, pp. X+637, ISBN 0-471-58986-1, MR 0822470, Zbl 1107.30300.
- ^ Evans, Lawrence C. (1998), Partial Differential Equations, American Mathematical Society.
- ^ a b c Lang, Serge (2003), Complex Analysis, Springer Verlag GTM, Springer Verlag
- ^ Rudin, Walter (1987), Real and complex analysis (3rd ed.), New York: McGraw–Hill Book Co., ISBN 978-0-07-054234-1, MR 0924157
- ^ Gunning and Rossi, Analytic Functions of Several Complex Variables, p. 2.
Further reading
[edit]External links
[edit]- "Analytic function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
















