This list of spirals includes named spirals that have been described mathematically.

Image	Name	First described	Equation	Comment
	circle		${\displaystyle r=k}$	The trivial spiral
	Archimedean spiral	c. 320 BC	${\displaystyle r=a+b\cdot \theta }$	Also known as the arithmetic spiral
	Euler spiral (also Cornu spiral or polynomial spiral)		${\displaystyle x(t)=\operatorname {C} (t),\,}$${\displaystyle y(t)=\operatorname {S} (t)}$	using Fresnel integrals[1]
	Fermat's spiral (also parabolic spiral)	1636[2]	${\displaystyle r^{2}=a^{2}\cdot \theta }$
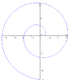
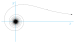
	hyperbolic spiral	1704	${\displaystyle r={\frac {a}{\theta ))}$	also reciprocal spiral
	lituus	1722	${\displaystyle r^{2}\cdot \theta =k}$
	logarithmic spiral	1638[3]	${\displaystyle r=a\cdot e^{b\cdot \theta ))$	Approximations of this are found in nature; also known as the equiangular spiral.
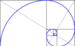
	Fibonacci spiral		circular arcs connecting the opposite corners of squares in the Fibonacci tiling	approximation of the golden spiral
	golden spiral		${\displaystyle r=\varphi ^{\frac {2\cdot \theta }{\pi ))\,}$	special case of the logarithmic spiral
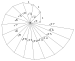
	Spiral of Theodorus			Also known as the Pythagorean spiral; an polygonal spiral composed of contiguous right triangles that approximates the Archimedean spiral
	involute	1673
	helix		${\displaystyle r(t)=1,\,}$ ${\displaystyle \theta (t)=t,\,}$ ${\displaystyle z(t)=t}$	a 3-dimensional spiral
	Rhumb line (also loxodrome)			type of spiral drawn on a sphere
	Cotes's spiral	1722	${\displaystyle {\frac {1}{r))={\begin{cases}A\cosh(k\theta +\varepsilon )\\A\exp(k\theta +\varepsilon )\\A\sinh(k\theta +\varepsilon )\\A(k\theta +\varepsilon )\\A\cos(k\theta +\varepsilon )\\\end{cases))}$	Solution to the two-body problem for an inverse-cube central force
	Poinsot's spirals		${\displaystyle r=a\cdot \operatorname {csch} (n\cdot \theta ),\,}$ ${\displaystyle r=a\cdot \operatorname {sech} (n\cdot \theta )}$
	Nielsen's spiral	1993[4]	${\displaystyle x(t)=\operatorname {ci} (t),\,}$ ${\displaystyle y(t)=\operatorname {si} (t)}$	A variation of Euler spiral, using sine integral and cosine integrals
	Polygonal spiral			special case approximation of logarithmic spiral
	Fraser's Spiral	1908		Optical illusion based on spirals
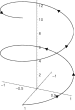
	Conchospiral		${\displaystyle r=\mu ^{t}\cdot a,\,}$${\displaystyle \theta =t,\,}$${\displaystyle z=\mu ^{t}\cdot c}$	three-dimensional spiral on the surface of a cone.
	Calkin–Wilf spiral
	Ulam spiral (also prime spiral)	1963
	Sack's spiral	1994		variant of Ulam spiral and Archimedean spiral.
	Seiffert's spiral	2000[5]	${\displaystyle r=\operatorname {sn} (s,k),\,}$${\displaystyle \theta =k\cdot s}$${\displaystyle z=\operatorname {cn} (s,k)}$	spiral curve on the surface of a sphere using the Jacobi elliptic functions[6]
	Tractrix spiral	1704[7]	${\displaystyle {\begin{cases}r=A\cos(t)\\\theta =\tan(t)-t\end{cases))}$
	Pappus spiral	1779	${\displaystyle {\begin{cases}r=a\theta \\\psi =k\end{cases))}$	3D conical spiral studied by Pappus and Pascal[8]
	doppler spiral		${\displaystyle x=a\cdot (t\cdot \cos(t)+k\cdot t),\,}$${\displaystyle y=a\cdot t\cdot \sin(t)}$	2D projection of Pappus spiral[9]
	Atzema spiral		${\displaystyle x={\frac {\sin(t)}{t))-2\cdot \cos(t)-t\cdot \sin(t),\,}$${\displaystyle y=-{\frac {\cos(t)}{t))-2\cdot \sin(t)+t\cdot \cos(t)}$	The curve that has a catacaustic forming a circle. Approximates the Archimedean spiral.[10]
	Atomic spiral	2002	${\displaystyle r={\frac {\theta }{\theta -a))}$	This spiral has two asymptotes; one is the circle of radius 1 and the other is the line ${\displaystyle \theta =a}$[11]
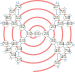
	Galactic spiral	2019	${\displaystyle {\begin{cases}dx=R*{\frac {y}{\sqrt {x^{2}+y^{2))))d\theta \\dy=R*{\Bigl [}\rho (\theta )-{\frac {x}{\sqrt {x^{2}+y^{2)))){\Bigr ]}d\theta \end{cases)){\begin{cases}x=\sum dx\\\\\\y=\sum dy+R\end{cases))}$	The differential spiral equations were developed to simulate the spiral arms of disc galaxies, have 4 solutions with three different cases:${\displaystyle \rho <1,\rho =1,\rho >1}$, the spiral patterns are decided by the behavior of the parameter ${\displaystyle \rho }$. For ${\displaystyle \rho <1}$, spiral-ring pattern; ${\displaystyle \rho =1,}$ regular spiral; ${\displaystyle \rho >1,}$ loose spiral. R is the distance of spiral starting point (0, R) to the center. The calculated x and y have to be rotated backward by (${\displaystyle -\theta }$) for plotting.[12]