Finding the direction of the cross product by the right-hand rule

In mathematics and physics, the right-hand rule is a common mnemonic for understanding the orientation of axes in three-dimensional space. It is also a convenient method for quickly finding the direction of the cross-product of 2 vectors. Rather than a mathematical fact, it is a convention, closely related to the convention that rotation around a vertical axis is positive if it is counterclockwise, and negative if it is clockwise.

Most of the various left-hand and right-hand rules arise from the fact that the three axes of three-dimensional space have two possible orientations.^[1] One can see this by holding one's hands outward and together, palms up, with the thumbs out-stretched to the right and left, and the fingers making a curling motion from straight outward to pointing upward. (Note the hand picture is not an illustration of this.) If the curling motion of the fingers represents a movement from the first (x-axis) to the second (y-axis), then the third (z-axis) can point along either thumb. Left-hand and right-hand rules arise when dealing with coordinate axes. The rule can be used to find the direction of the magnetic field, rotation, spirals, electromagnetic fields, mirror images, and enantiomers in mathematics and chemistry.

The sequence is often: index finger, middle finger, thumb. Two other sequences also work because they preserve the cycle:

• Middle finger, thumb, index finger.
• Thumb, index finger, middle finger (e.g., see the ninth series of the Swiss 200-francs banknote).^{[citation needed]}

Curve orientation and normal vectors

In vector calculus, it is necessary to relate the normal vector to a surface to the curve bounding it. For a positively-oriented curve C, bounding a surface S, the normal to the surface n̂ is defined such that the right thumb points in the direction of n̂, and the fingers curl along the orientation of the bounding curve C.

Right-hand rule for curve orientation.

Coordinates

Left-handed coordinates on the left,
right-handed coordinates on the right.

Coordinates are usually right-handed.

For right-handed coordinates, the right thumb points along the z-axis in the positive direction and the curling motion of the fingers of the right hand represents a motion from the first or x-axis to the second or y-axis. When viewed from the top or z-axis the system is counter-clockwise.

For left-handed coordinates, the left thumb points along the z-axis in the positive direction and the curling motion of the fingers of the left hand represents a motion from the first or x-axis to the second or y-axis. When viewed from the top or z-axis the system is clockwise.

Interchanging the labels of any two axes reverses the handedness. Reversing the direction of one axis (or of all three axes) also reverses the handedness. (If the axes do not have a positive or negative direction then handedness has no meaning.) Reversing two axes amounts to a 180° rotation around the remaining axis.^[2]

Rotations

A rotating body

Conventional direction of the axis of a rotating body

In mathematics, a rotating body is commonly represented by a pseudovector along the axis of rotation. The length of the vector gives the speed of rotation and the direction of the axis gives the direction of rotation according to the right-hand rule: right fingers curled in the direction of rotation and the right thumb pointing in the positive direction of the axis. This allows some easy calculations using the vector cross-product. No part of the body is moving in the direction of the axis arrow. By coincidence, if the thumb is pointing north, Earth rotates in a prograde direction according to the right-hand rule. This causes the Sun, Moon, and stars to appear to revolve westward according to the left-hand rule.

Helices and screws

Left- and right-handed screws

A helix is a curved line formed by a point rotating around a center while the center moves up or down the z-axis. Helices are either right- or left-handed, with curled fingers giving the direction of rotation and thumb giving the direction of advance along the z-axis.

The threads of a screw are helix and therefore screws can be right- or left-handed. The rule is this: if a screw is right-handed (most screws are) point your right thumb in the direction you want the screw to go and turn the screw in the direction of your curled right fingers.

Electromagnetism

• When electricity (conventional current) flows in a long straight wire, it creates a circular or cylindrical magnetic field around the wire according to the right-hand rule. The conventional current, which is the opposite of the actual flow of electrons, is a flow of positive charges along the positive z-axis. The conventional direction of a magnetic line is given by a compass needle.
• Electromagnet: The magnetic field around a wire is quite weak. If the wire is coiled into a helix, all the field lines inside the helix point in the same direction and each successive coil reinforces the others. The advance of the helix, the non-circular part of the current, and the field lines all point in the positive z direction. Since there is no magnetic monopole, the field lines exit the +z end, loop around outside the helix, and re-enter at the −z end. The +z end where the lines exit is defined as the north pole. If the fingers of the right hand are curled in the direction of the circular component of the current, the right thumb points to the north pole.
• Lorentz force: If a positive electric charge moves across a magnetic field, it experiences a force according to Lorentz force, with the direction given by the right-hand rule. If the curl of the right fingers represents a rotation from the direction the charge is moving to the direction of the magnetic field, then the force is in the direction of the right thumb. Because the charge is moving, the force causes the particle path to bend. The bending force is computed by the vector cross-product. This means that the bending force increases with the velocity of the particle and the strength of the magnetic field. The force is maximum when the particle direction and magnetic fields are at right angles, is less at any other angle and is zero when the particle moves parallel to the field.

Ampère's right-hand grip rule

Prediction of direction of field (B), given that the current I flows in the direction of the thumb

Finding direction of magnetic field (B) for an electrical coil

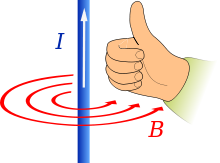
Ampère's right-hand grip rule^[3] (also called the right-hand screw rule, coffee-mug rule or the corkscrew-rule) is used either when a vector (such as the Euler vector) must be defined to represent the rotation of a body, a magnetic field, or a fluid, or vice versa, when it is necessary to define a rotation vector to understand how rotation occurs. It reveals a connection between the current and the magnetic field lines in the magnetic field that the current created.

André-Marie Ampère, a French physicist and mathematician, for whom the rule was named, was inspired by Hans Christian Ørsted, another physicist who experimented with magnet needles. Ørsted observed that the needles swirled when in the proximity of an electric current-carrying wire, and concluded that electricity could create magnetic fields.

Application

This rule is used in two different applications of Ampère's circuital law:

1. An electric current passes through a straight wire. When the thumb is pointed in the direction of conventional current (from positive to negative), the curled fingers will then point in the direction of the magnetic flux lines around the conductor. The direction of the magnetic field (counterclockwise rotation instead of clockwise rotation of coordinates when viewing the tip of the thumb) is a result of this convention and not an underlying physical phenomenon.
2. An electric current passes through a solenoid, resulting in a magnetic field. When wrapping the right hand around the solenoid with the fingers in the direction of the conventional current, the thumb points in the direction of the magnetic north pole.

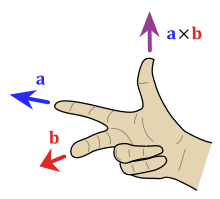
Cross products

Illustration of the right-hand rule on the ninth series of the Swiss 200-francs banknote.

The cross product of two vectors is often taken in physics and engineering. For example, in statics and dynamics, torque is the cross product of lever length and force, while angular momentum is the cross product of distance and linear momentum. In electricity and magnetism, the force exerted on a moving charged particle when moving in a magnetic field B is given by:

${\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }$

The direction of the cross product may be found by application of the right-hand rule as follows:

1. The index finger points in the direction of the velocity vector v.
2. The middle finger points in the direction of the magnetic field vector B.
3. The thumb points in the direction of the cross product F.

For example, for a positively charged particle moving to the north, in a region where the magnetic field points west, the resultant force points up.^[2]

Applications

The right-hand rule has widespread use in physics. A list of physical quantities whose directions are related by the right-hand rule is given below. (Some of these are related only indirectly to cross products, and use the second form.)

• For a rotating object, if the right-hand fingers follow the curve of a point on the object, then the thumb points along the axis of rotation in the direction of the angular velocity vector.
• A torque, the force that causes it, and the position of the point of application of the force.
• A magnetic field, the position of the point where it is determined, and the electric current (or change in electric flux) that causes it.
• A magnetic field in a coil of wire and the electric current in the wire.
• The force of a magnetic field on a charged particle, the magnetic field itself, and the velocity of the object.
• The vorticity at any point in the field of the flow of a fluid
• The induced current from motion in a magnetic field (known as Fleming's right-hand rule).
• The x, y and z unit vectors in a Cartesian coordinate system can be chosen to follow the right-hand rule. Right-handed coordinate systems are often used in rigid body and kinematics.