| Secure Hash Algorithms | |
|---|---|
| Concepts | |
| hash functions, SHA, DSA | |
| Main standards | |
| SHA-0, SHA-1, SHA-2, SHA-3 | |
| General | |
|---|---|
| Designers | National Security Agency |
| First published | 1993 (SHA-0), 1995 (SHA-1) |
| Series | (SHA-0), SHA-1, SHA-2, SHA-3 |
| Certification | FIPS PUB 180-4, CRYPTREC (Monitored) |
| Cipher detail | |
| Digest sizes | 160 bits |
| Block sizes | 512 bits |
| Structure | Merkle–Damgård construction |
| Rounds | 80 |
| Best public cryptanalysis | |
| A 2011 attack by Marc Stevens can produce hash collisions with a complexity between 260.3 and 265.3 operations.[1] The first public collision was published on 23 February 2017.[2] SHA-1 is prone to length extension attacks. | |
In cryptography, SHA-1 (Secure Hash Algorithm 1) is a hash function which takes an input and produces a 160-bit (20-byte) hash value known as a message digest – typically rendered as 40 hexadecimal digits. It was designed by the United States National Security Agency, and is a U.S. Federal Information Processing Standard.[3] The algorithm has been cryptographically broken[4][5][6][7][8][9][10] but is still widely used.
Since 2005, SHA-1 has not been considered secure against well-funded opponents;[11] as of 2010 many organizations have recommended its replacement.[12][10][13] NIST formally deprecated use of SHA-1 in 2011 and disallowed its use for digital signatures in 2013, and declared that it should be phased out by 2030.[14] As of 2020[update], chosen-prefix attacks against SHA-1 are practical.[6][8] As such, it is recommended to remove SHA-1 from products as soon as possible and instead use SHA-2 or SHA-3. Replacing SHA-1 is urgent where it is used for digital signatures.
All major web browser vendors ceased acceptance of SHA-1 SSL certificates in 2017.[15][9][4] In February 2017, CWI Amsterdam and Google announced they had performed a collision attack against SHA-1, publishing two dissimilar PDF files which produced the same SHA-1 hash.[16][2] However, SHA-1 is still secure for HMAC.[17]
Microsoft has discontinued SHA-1 code signing support for Windows Update on August 3, 2020,[18] which also effectively ended the update servers for versions of Windows that have not been updated to SHA-2, such as Windows 2000 up to Vista, as well as Windows Server versions from Windows 2000 Server to Server 2003.
Development
[edit]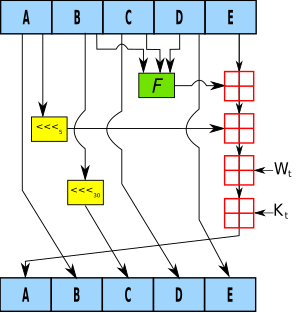
- A, B, C, D and E are 32-bit words of the state;
- F is a nonlinear function that varies;
- denotes a left bit rotation by n places;
- n varies for each operation;
- Wt is the expanded message word of round t;
- Kt is the round constant of round t;
 denotes addition modulo 232.
denotes addition modulo 232.
SHA-1 produces a message digest based on principles similar to those used by Ronald L. Rivest of MIT in the design of the MD2, MD4 and MD5 message digest algorithms, but generates a larger hash value (160 bits vs. 128 bits).
SHA-1 was developed as part of the U.S. Government's Capstone project.[19] The original specification of the algorithm was published in 1993 under the title Secure Hash Standard, FIPS PUB 180, by U.S. government standards agency NIST (National Institute of Standards and Technology).[20][21] This version is now often named SHA-0. It was withdrawn by the NSA shortly after publication and was superseded by the revised version, published in 1995 in FIPS PUB 180-1 and commonly designated SHA-1. SHA-1 differs from SHA-0 only by a single bitwise rotation in the message schedule of its compression function. According to the NSA, this was done to correct a flaw in the original algorithm which reduced its cryptographic security, but they did not provide any further explanation.[22][23] Publicly available techniques did indeed demonstrate a compromise of SHA-0, in 2004, before SHA-1 in 2017 (see §Attacks).
Applications
[edit]Cryptography
[edit]SHA-1 forms part of several widely used security applications and protocols, including TLS and SSL, PGP, SSH, S/MIME, and IPsec. Those applications can also use MD5; both MD5 and SHA-1 are descended from MD4.
SHA-1 and SHA-2 are the hash algorithms required by law for use in certain U.S. government applications, including use within other cryptographic algorithms and protocols, for the protection of sensitive unclassified information. FIPS PUB 180-1 also encouraged adoption and use of SHA-1 by private and commercial organizations. SHA-1 is being retired from most government uses; the U.S. National Institute of Standards and Technology said, "Federal agencies should stop using SHA-1 for...applications that require collision resistance as soon as practical, and must use the SHA-2 family of hash functions for these applications after 2010",[24] though that was later relaxed to allow SHA-1 to be used for verifying old digital signatures and time stamps.[25]
A prime motivation for the publication of the Secure Hash Algorithm was the Digital Signature Standard, in which it is incorporated.
The SHA hash functions have been used for the basis of the SHACAL block ciphers.
Data integrity
[edit]Revision control systems such as Git, Mercurial, and Monotone use SHA-1, not for security, but to identify revisions and to ensure that the data has not changed due to accidental corruption. Linus Torvalds said about Git in 2007:
- If you have disk corruption, if you have DRAM corruption, if you have any kind of problems at all, Git will notice them. It's not a question of if, it's a guarantee. You can have people who try to be malicious. They won't succeed. [...] Nobody has been able to break SHA-1, but the point is the SHA-1, as far as Git is concerned, isn't even a security feature. It's purely a consistency check. The security parts are elsewhere, so a lot of people assume that since Git uses SHA-1 and SHA-1 is used for cryptographically secure stuff, they think that, Okay, it's a huge security feature. It has nothing at all to do with security, it's just the best hash you can get. ...
- I guarantee you, if you put your data in Git, you can trust the fact that five years later, after it was converted from your hard disk to DVD to whatever new technology and you copied it along, five years later you can verify that the data you get back out is the exact same data you put in. [...]
- One of the reasons I care is for the kernel, we had a break in on one of the BitKeeper sites where people tried to corrupt the kernel source code repositories.[26]
However Git does not require the second preimage resistance of SHA-1 as a security feature, since it will always prefer to keep the earliest version of an object in case of collision, preventing an attacker from surreptitiously overwriting files.[27] The known attacks (as of 2020) also do not break second preimage resistance.[28]
Cryptanalysis and validation
[edit]For a hash function for which L is the number of bits in the message digest, finding a message that corresponds to a given message digest can always be done using a brute force search in approximately 2L evaluations. This is called a preimage attack and may or may not be practical depending on L and the particular computing environment. However, a collision, consisting of finding two different messages that produce the same message digest, requires on average only about 1.2 × 2L/2 evaluations using a birthday attack. Thus the strength of a hash function is usually compared to a symmetric cipher of half the message digest length. SHA-1, which has a 160-bit message digest, was originally thought to have 80-bit strength.
Some of the applications that use cryptographic hashes, like password storage, are only minimally affected by a collision attack. Constructing a password that works for a given account requires a preimage attack, as well as access to the hash of the original password, which may or may not be trivial. Reversing password encryption (e.g. to obtain a password to try against a user's account elsewhere) is not made possible by the attacks. However, even a secure password hash can't prevent brute-force attacks on weak passwords. See Password cracking.
In the case of document signing, an attacker could not simply fake a signature from an existing document: The attacker would have to produce a pair of documents, one innocuous and one damaging, and get the private key holder to sign the innocuous document. There are practical circumstances in which this is possible; until the end of 2008, it was possible to create forged SSL certificates using an MD5 collision.[29]
Due to the block and iterative structure of the algorithms and the absence of additional final steps, all SHA functions (except SHA-3)[30] are vulnerable to length-extension and partial-message collision attacks.[31] These attacks allow an attacker to forge a message signed only by a keyed hash – SHA(message || key) or SHA(key || message) – by extending the message and recalculating the hash without knowing the key. A simple improvement to prevent these attacks is to hash twice: SHAd(message) = SHA(SHA(0b || message)) (the length of 0b, zero block, is equal to the block size of the hash function).
SHA-0
[edit]At CRYPTO 98, two French researchers, Florent Chabaud and Antoine Joux, presented an attack on SHA1: collisions can be found with complexity 261, fewer than the 280 for an ideal hash function of the same size.[32]
In 2004, Biham and Chen found near-collisions for SHA-0 – two messages that hash to nearly the same value; in this case, 142 out of the 160 bits are equal. They also found full collisions of SHA-0 reduced to 62 out of its 80 rounds.[33]
Subsequently, on 12 August 2004, a collision for the full SHA-0 algorithm was announced by Joux, Carribault, Lemuet, and Jalby. This was done by using a generalization of the Chabaud and Joux attack. Finding the collision had complexity 251 and took about 80,000 processor-hours on a supercomputer with 256 Itanium 2 processors (equivalent to 13 days of full-time use of the computer).
On 17 August 2004, at the Rump Session of CRYPTO 2004, preliminary results were announced by Wang, Feng, Lai, and Yu, about an attack on MD5, SHA-0 and other hash functions. The complexity of their attack on SHA-0 is 240, significantly better than the attack by Joux et al.[34][35]
In February 2005, an attack by Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu was announced which could find collisions in SHA-0 in 239 operations.[5][36]
Another attack in 2008 applying the boomerang attack brought the complexity of finding collisions down to 233.6, which was estimated to take 1 hour on an average PC from the year 2008.[37]
In light of the results for SHA-0, some experts[who?] suggested that plans for the use of SHA-1 in new cryptosystems should be reconsidered. After the CRYPTO 2004 results were published, NIST announced that they planned to phase out the use of SHA-1 by 2010 in favor of the SHA-2 variants.[38]
Attacks
[edit]In early 2005, Vincent Rijmen and Elisabeth Oswald published an attack on a reduced version of SHA-1 – 53 out of 80 rounds – which finds collisions with a computational effort of fewer than 280 operations.[39]
In February 2005, an attack by Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu was announced.[5] The attacks can find collisions in the full version of SHA-1, requiring fewer than 269 operations. (A brute-force search would require 280 operations.)
The authors write: "In particular, our analysis is built upon the original differential attack on SHA-0, the near collision attack on SHA-0, the multiblock collision techniques, as well as the message modification techniques used in the collision search attack on MD5. Breaking SHA-1 would not be possible without these powerful analytical techniques."[40] The authors have presented a collision for 58-round SHA-1, found with 233 hash operations. The paper with the full attack description was published in August 2005 at the CRYPTO conference.
In an interview, Yin states that, "Roughly, we exploit the following two weaknesses: One is that the file preprocessing step is not complicated enough; another is that certain math operations in the first 20 rounds have unexpected security problems."[41]
On 17 August 2005, an improvement on the SHA-1 attack was announced on behalf of Xiaoyun Wang, Andrew Yao and Frances Yao at the CRYPTO 2005 Rump Session, lowering the complexity required for finding a collision in SHA-1 to 263.[7] On 18 December 2007 the details of this result were explained and verified by Martin Cochran.[42]
Christophe De Cannière and Christian Rechberger further improved the attack on SHA-1 in "Finding SHA-1 Characteristics: General Results and Applications,"[43] receiving the Best Paper Award at ASIACRYPT 2006. A two-block collision for 64-round SHA-1 was presented, found using unoptimized methods with 235 compression function evaluations. Since this attack requires the equivalent of about 235 evaluations, it is considered to be a significant theoretical break.[44] Their attack was extended further to 73 rounds (of 80) in 2010 by Grechnikov.[45] In order to find an actual collision in the full 80 rounds of the hash function, however, tremendous amounts of computer time are required. To that end, a collision search for SHA-1 using the volunteer computing platform BOINC began August 8, 2007, organized by the Graz University of Technology. The effort was abandoned May 12, 2009 due to lack of progress.[46]
At the Rump Session of CRYPTO 2006, Christian Rechberger and Christophe De Cannière claimed to have discovered a collision attack on SHA-1 that would allow an attacker to select at least parts of the message.[47][48]
In 2008, an attack methodology by Stéphane Manuel reported hash collisions with an estimated theoretical complexity of 251 to 257 operations.[49] However he later retracted that claim after finding that local collision paths were not actually independent, and finally quoting for the most efficient a collision vector that was already known before this work.[50]
Cameron McDonald, Philip Hawkes and Josef Pieprzyk presented a hash collision attack with claimed complexity 252 at the Rump Session of Eurocrypt 2009.[51] However, the accompanying paper, "Differential Path for SHA-1 with complexity O(252)" has been withdrawn due to the authors' discovery that their estimate was incorrect.[52]
One attack against SHA-1 was Marc Stevens[53] with an estimated cost of $2.77M (2012) to break a single hash value by renting CPU power from cloud servers.[54] Stevens developed this attack in a project called HashClash,[55] implementing a differential path attack. On 8 November 2010, he claimed he had a fully working near-collision attack against full SHA-1 working with an estimated complexity equivalent to 257.5 SHA-1 compressions. He estimated this attack could be extended to a full collision with a complexity around 261.
The SHAppening
[edit]On 8 October 2015, Marc Stevens, Pierre Karpman, and Thomas Peyrin published a freestart collision attack on SHA-1's compression function that requires only 257 SHA-1 evaluations. This does not directly translate into a collision on the full SHA-1 hash function (where an attacker is not able to freely choose the initial internal state), but undermines the security claims for SHA-1. In particular, it was the first time that an attack on full SHA-1 had been demonstrated; all earlier attacks were too expensive for their authors to carry them out. The authors named this significant breakthrough in the cryptanalysis of SHA-1 The SHAppening.[10]
The method was based on their earlier work, as well as the auxiliary paths (or boomerangs) speed-up technique from Joux and Peyrin, and using high performance/cost efficient GPU cards from Nvidia. The collision was found on a 16-node cluster with a total of 64 graphics cards. The authors estimated that a similar collision could be found by buying US$2,000 of GPU time on EC2.[10]
The authors estimated that the cost of renting enough of EC2 CPU/GPU time to generate a full collision for SHA-1 at the time of publication was between US$75K and $120K, and noted that was well within the budget of criminal organizations, not to mention national intelligence agencies. As such, the authors recommended that SHA-1 be deprecated as quickly as possible.[10]
SHAttered – first public collision
[edit]On 23 February 2017, the CWI (Centrum Wiskunde & Informatica) and Google announced the SHAttered attack, in which they generated two different PDF files with the same SHA-1 hash in roughly 263.1 SHA-1 evaluations. This attack is about 100,000 times faster than brute forcing a SHA-1 collision with a birthday attack, which was estimated to take 280 SHA-1 evaluations. The attack required "the equivalent processing power of 6,500 years of single-CPU computations and 110 years of single-GPU computations".[2]
Birthday-Near-Collision Attack – first practical chosen-prefix attack
[edit]On 24 April 2019 a paper by Gaëtan Leurent and Thomas Peyrin presented at Eurocrypt 2019 described an enhancement to the previously best chosen-prefix attack in Merkle–Damgård–like digest functions based on Davies–Meyer block ciphers. With these improvements, this method is capable of finding chosen-prefix collisions in approximately 268 SHA-1 evaluations. This is approximately 1 billion times faster (and now usable for many targeted attacks, thanks to the possibility of choosing a prefix, for example malicious code or faked identities in signed certificates) than the previous attack's 277.1 evaluations (but without chosen prefix, which was impractical for most targeted attacks because the found collisions were almost random)[1] and is fast enough to be practical for resourceful attackers, requiring approximately $100,000 of cloud processing. This method is also capable of finding chosen-prefix collisions in the MD5 function, but at a complexity of 246.3 does not surpass the prior best available method at a theoretical level (239), though potentially at a practical level (≤249).[56] This attack has a memory requirement of 500+ GB.
On 5 January 2020 the authors published an improved attack called "shambles".[8] In this paper they demonstrate a chosen-prefix collision attack with a complexity of 263.4, that at the time of publication would cost US$45K per generated collision.
Official validation
[edit]Implementations of all FIPS-approved security functions can be officially validated through the CMVP program, jointly run by the National Institute of Standards and Technology (NIST) and the Communications Security Establishment (CSE). For informal verification, a package to generate a high number of test vectors is made available for download on the NIST site; the resulting verification, however, does not replace the formal CMVP validation, which is required by law for certain applications.
As of December 2013[update], there are over 2000 validated implementations of SHA-1, with 14 of them capable of handling messages with a length in bits not a multiple of eight (see SHS Validation List Archived 2011-08-23 at the Wayback Machine).
Examples and pseudocode
[edit]Example hashes
[edit]These are examples of SHA-1 message digests in hexadecimal and in Base64 binary to ASCII text encoding.
SHA1("The quick brown fox jumps over the lazy dog")
Even a small change in the message will, with overwhelming probability, result in many bits changing due to the avalanche effect. For example, changing dog to cog produces a hash with different values for 81 of the 160 bits:
SHA1("The quick brown fox jumps over the lazy cog")
The hash of the zero-length string is:
SHA1("")
SHA-1 pseudocode
[edit]Pseudocode for the SHA-1 algorithm follows:
Note 1: All variables are unsigned 32-bit quantities and wrap modulo 232 when calculating, except for ml, the message length, which is a 64-bit quantity, and hh, the message digest, which is a 160-bit quantity. Note 2: All constants in this pseudo code are in big endian. Within each word, the most significant byte is stored in the leftmost byte position Initialize variables: h0 = 0x67452301 h1 = 0xEFCDAB89 h2 = 0x98BADCFE h3 = 0x10325476 h4 = 0xC3D2E1F0 ml = message length in bits (always a multiple of the number of bits in a character). Pre-processing: append the bit '1' to the message e.g. by adding 0x80 if message length is a multiple of 8 bits. append 0 ≤ k < 512 bits '0', such that the resulting message length in bits is congruent to −64 ≡ 448 (mod 512) append ml, the original message length in bits, as a 64-bit big-endian integer. Thus, the total length is a multiple of 512 bits. Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk break chunk into sixteen 32-bit big-endian words w[i], 0 ≤ i ≤ 15 Message schedule: extend the sixteen 32-bit words into eighty 32-bit words: for i from 16 to 79 Note 3: SHA-0 differs by not having this leftrotate. w[i] = (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1 Initialize hash value for this chunk: a = h0 b = h1 c = h2 d = h3 e = h4 Main loop:[3][57] for i from 0 to 79 if 0 ≤ i ≤ 19 then f = (b and c) or ((not b) and d) k = 0x5A827999 else if 20 ≤ i ≤ 39 f = b xor c xor d k = 0x6ED9EBA1 else if 40 ≤ i ≤ 59 f = (b and c) or (b and d) or (c and d) k = 0x8F1BBCDC else if 60 ≤ i ≤ 79 f = b xor c xor d k = 0xCA62C1D6 temp = (a leftrotate 5) + f + e + k + w[i] e = d d = c c = b leftrotate 30 b = a a = temp Add this chunk's hash to result so far: h0 = h0 + a h1 = h1 + b h2 = h2 + c h3 = h3 + d h4 = h4 + e Produce the final hash value (big-endian) as a 160-bit number: hh = (h0 leftshift 128) or (h1 leftshift 96) or (h2 leftshift 64) or (h3 leftshift 32) or h4
The number hh is the message digest, which can be written in hexadecimal (base 16).
The chosen constant values used in the algorithm were assumed to be nothing up my sleeve numbers:
- The four round constants
kare 230 times the square roots of 2, 3, 5 and 10. However they were incorrectly rounded to the nearest integer instead of being rounded to the nearest odd integer, with equilibrated proportions of zero and one bits. As well, choosing the square root of 10 (which is not a prime) made it a common factor for the two other chosen square roots of primes 2 and 5, with possibly usable arithmetic properties across successive rounds, reducing the strength of the algorithm against finding collisions on some bits. - The first four starting values for
h0throughh3are the same with the MD5 algorithm, and the fifth (forh4) is similar. However they were not properly verified for being resistant against inversion of the few first rounds to infer possible collisions on some bits, usable by multiblock differential attacks.
Instead of the formulation from the original FIPS PUB 180-1 shown, the following equivalent expressions may be used to compute f in the main loop above:
Bitwise choice between c and d, controlled by b. (0 ≤ i ≤ 19): f = d xor (b and (c xor d)) (alternative 1) (0 ≤ i ≤ 19): f = (b and c) or ((not b) and d) (alternative 2) (0 ≤ i ≤ 19): f = (b and c) xor ((not b) and d) (alternative 3) (0 ≤ i ≤ 19): f = vec_sel(d, c, b) (alternative 4) [premo08] Bitwise majority function. (40 ≤ i ≤ 59): f = (b and c) or (d and (b or c)) (alternative 1) (40 ≤ i ≤ 59): f = (b and c) or (d and (b xor c)) (alternative 2) (40 ≤ i ≤ 59): f = (b and c) xor (d and (b xor c)) (alternative 3) (40 ≤ i ≤ 59): f = (b and c) xor (b and d) xor (c and d) (alternative 4) (40 ≤ i ≤ 59): f = vec_sel(c, b, c xor d) (alternative 5)
It was also shown[58] that for the rounds 32–79 the computation of:
w[i] = (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1
can be replaced with:
w[i] = (w[i-6] xor w[i-16] xor w[i-28] xor w[i-32]) leftrotate 2
This transformation keeps all operands 64-bit aligned and, by removing the dependency of w[i] on w[i-3], allows efficient SIMD implementation with a vector length of 4 like x86 SSE instructions.
Comparison of SHA functions
[edit]In the table below, internal state means the "internal hash sum" after each compression of a data block.
| Algorithm and variant | Output size (bits) |
Internal state size (bits) |
Block size (bits) |
Rounds | Operations | Security against collision attacks (bits) |
Security against length extension attacks (bits) |
Performance on Skylake (median cpb)[59] | First published | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Long messages | 8 bytes | ||||||||||
| MD5 (as reference) | 128 | 128 (4 × 32) |
512 | 4 (16 operations in each round) |
And, Xor, Or, Rot, Add (mod 232) | ≤ 18 (collisions found)[60] |
0 | 4.99 | 55.00 | 1992 | |
| SHA-0 | 160 | 160 (5 × 32) |
512 | 80 | And, Xor, Or, Rot, Add (mod 232) | < 34 (collisions found) |
0 | ≈ SHA-1 | ≈ SHA-1 | 1993 | |
| SHA-1 | < 63 (collisions found)[61] |
3.47 | 52.00 | 1995 | |||||||
| SHA-2 | SHA-224 SHA-256 |
224 256 |
256 (8 × 32) |
512 | 64 | And, Xor, Or, Rot, Shr, Add (mod 232) |
112 128 |
32 0 |
7.62 7.63 |
84.50 85.25 |
2004 2001 |
| SHA-384 | 384 | 512 (8 × 64) |
1024 | 80 | And, Xor, Or, Rot, Shr, Add (mod 264) |
192 | 128 | 5.12 | 135.75 | 2001 | |
| SHA-512 | 512 | 256 | 0[62] | 5.06 | 135.50 | 2001 | |||||
| SHA-512/224 SHA-512/256 |
224 256 |
112 128 |
288 256 |
≈ SHA-384 | ≈ SHA-384 | 2012 | |||||
| SHA-3 | SHA3-224 SHA3-256 SHA3-384 SHA3-512 |
224 256 384 512 |
1600 (5 × 5 × 64) |
1152 1088 832 576 |
24[63] | And, Xor, Rot, Not | 112 128 192 256 |
448 512 768 1024 |
8.12 8.59 11.06 15.88 |
154.25 155.50 164.00 164.00 |
2015 |
| SHAKE128 SHAKE256 |
d (arbitrary) d (arbitrary) |
1344 1088 |
min(d/2, 128) min(d/2, 256) |
256 512 |
7.08 8.59 |
155.25 155.50 | |||||
Implementations
[edit]Below is a list of cryptography libraries that support SHA-1:
Hardware acceleration is provided by the following processor extensions:
- Intel SHA extensions: Available on some Intel and AMD x86 processors.
- VIA PadLock
- IBM z/Architecture: Available since 2003 as part of the Message-Security-Assist Extension[64]
Collision countermeasure
[edit]In the wake of SHAttered, Mark Stevens and Dan Shumow published "sha1collisiondetection" (SHA-1CD), a variant of SHA-1 that detects collision attacks and changes the hash output when one is detected. The false positive rate is 2-90.[65] SHA-1CD is used by GitHub since March 2017 and git since version 2.13.0 of May 2017.[66]
See also
[edit]- Comparison of cryptographic hash functions
- Hash function security summary
- International Association for Cryptologic Research
- Secure Hash Standard
Notes
[edit]- ^ a b Stevens, Marc (June 19, 2012). Attacks on Hash Functions and Applications (PDF) (PhD thesis). Leiden University. hdl:1887/19093. ISBN 9789461913173. OCLC 795702954.
- ^ a b c Stevens, Marc; Bursztein, Elie; Karpman, Pierre; Albertini, Ange; Markov, Yarik (2017). Katz, Jonathan; Shacham, Hovav (eds.). The First Collision for Full SHA-1 (PDF). Advances in Cryptology – CRYPTO 2017. Lecture Notes in Computer Science. Vol. 10401. Springer. pp. 570–596. doi:10.1007/978-3-319-63688-7_19. ISBN 9783319636870. Archived from the original (PDF) on May 15, 2018. Retrieved February 23, 2017.
- Marc Stevens; Elie Bursztein; Pierre Karpman; Ange Albertini; Yarik Markov; Alex Petit Bianco; Clement Baisse (February 23, 2017). "Announcing the first SHA1 collision". Google Security Blog.
- ^ a b "Secure Hash Standard (SHS)" (PDF). National Institute of Standards and Technology. 2015. doi:10.6028/NIST.FIPS.180-4. Federal Information Processing Standards Publication 180-4. Archived from the original (PDF) on 2020-01-07. Retrieved 2019-09-23.
- ^ a b "The end of SHA-1 on the Public Web". Mozilla Security Blog. 23 February 2017. Retrieved 2019-05-29.
- ^ a b c "SHA-1 Broken – Schneier on Security". www.schneier.com.
- ^ a b "Critical flaw demonstrated in common digital security algorithm". Nanyang Technological University, Singapore. 24 January 2020.
- ^ a b "New Cryptanalytic Results Against SHA-1 – Schneier on Security". www.schneier.com.
- ^ a b c Leurent, Gaëtan; Peyrin, Thomas (2020-01-05). "SHA-1 is a Shambles First Chosen-Prefix Collision on SHA-1 and Application to the PGP Web of Trust" (PDF). Cryptology ePrint Archive, Report 2020/014.
- ^ a b "Google will drop SHA-1 encryption from Chrome by January 1, 2017". VentureBeat. 2015-12-18. Retrieved 2019-05-29.
- ^ a b c d e Stevens, Marc; Karpman, Pierre; Peyrin, Thomas. "The SHAppening: freestart collisions for SHA-1". Retrieved 2015-10-09.
- ^ Schneier, Bruce (February 18, 2005). "Schneier on Security: Cryptanalysis of SHA-1".
- ^ "NIST.gov – Computer Security Division – Computer Security Resource Center". Archived from the original on 2011-06-25. Retrieved 2019-01-05.
- ^ Schneier, Bruce (8 October 2015). "SHA-1 Freestart Collision". Schneier on Security.
- ^ "NIST Retires SHA-1 Cryptographic Algorithm" (Press release). NIST. 2022-12-15.
- ^ Goodin, Dan (2016-05-04). "Microsoft to retire support for SHA1 certificates in the next 4 months". Ars Technica. Retrieved 2019-05-29.
- ^ "CWI, Google announce first collision for Industry Security Standard SHA-1". Retrieved 2017-02-23.
- ^ Barker, Elaine (May 2020). Recommendation for Key Management: Part 1 – General, Table 3 (Technical Report). NIST. p. 56. doi:10.6028/NIST.SP.800-57pt1r5.
- ^ "SHA-1 Windows content to be retired August 3, 2020". techcommunity.microsoft.com. Retrieved 2024-02-28.
- ^ "RSA FAQ on Capstone".
- ^ Selvarani, R.; Aswatha, Kumar; T V Suresh, Kumar (2012). Proceedings of International Conference on Advances in Computing. Springer Science & Business Media. p. 551. ISBN 978-81-322-0740-5.
- ^ Secure Hash Standard, Federal Information Processing Standards Publication FIPS PUB 180, National Institute of Standards and Technology, 11 May 1993
- ^ Kramer, Samuel (11 July 1994). "Proposed Revision of Federal Information Processing Standard (FIPS) 180, Secure Hash Standard". Federal Register.
- ^ fgrieu. "Where can I find a description of the SHA-0 hash algorithm?". Cryptography Stack Exchange.
- ^ Computer Security Division, Information Technology Laboratory (2017-01-04). "NIST Policy on Hash Functions – Hash Functions". CSRC, NIST. Retrieved 2023-08-27.
- ^ Computer Security Division, Information Technology Laboratory (2017-01-04). "NIST Policy on Hash Functions – Hash Functions". CSRC, NIST. Retrieved 2023-08-27.
- ^ "Tech Talk: Linus Torvalds on git". YouTube. Retrieved November 13, 2013.
- ^ Torvalds, Linus. "Re: Starting to think about sha-256?". marc.info. Retrieved 30 May 2016.
- ^ Walfield, Neal H. (2020). "openpgp: Pass the hash algo's security reqs to Policy::signature". gitlab.com/sequoia-pgp. – see section "Background" in the rendered documentation
- ^ Sotirov, Alexander; Stevens, Marc; Appelbaum, Jacob; Lenstra, Arjen; Molnar, David; Osvik, Dag Arne; de Weger, Benne (December 30, 2008). "MD5 considered harmful today: Creating a rogue CA certificate". Retrieved March 29, 2009.
- ^ "Strengths of Keccak – Design and security". The Keccak sponge function family. Keccak team. Retrieved 20 September 2015.
Unlike SHA-1 and SHA-2, Keccak does not have the length-extension weakness, hence does not need the HMAC nested construction. Instead, MAC computation can be performed by simply prepending the message with the key.
- ^ "Schneier on Security: Cryptography Engineering". www.schneier.com. Retrieved 2023-08-27.
- ^ Chabaud, Florent; Joux, Antoine (October 3, 1998). "Differential collisions in SHA-0". In Krawczyk, Hugo (ed.). Advances in Cryptology – CRYPTO '98. Lecture Notes in Computer Science. Vol. 1462. Springer. pp. 56–71. doi:10.1007/BFb0055720. ISBN 978-3-540-64892-5 – via Springer Link.
- ^ Biham, Eli; Chen, Rafi. "Near-Collisions of SHA-0" (PDF).
- ^ "Report from Crypto 2004". Archived from the original on 2004-08-21. Retrieved 2004-08-23.
- ^ Grieu, Francois (18 August 2004). "Re: Any advance news from the crypto rump session?". Newsgroup: sci.crypt. Event occurs at 05:06:02 +0200. Usenet: fgrieu-05A994.05060218082004@individual.net.
- ^ Efficient Collision Search Attacks on SHA-0 Archived 2005-09-10 at the Wayback Machine, Shandong University
- ^ Manuel, Stéphane; Peyrin, Thomas (2008-02-11). Collisions on SHA-0 in One Hour (PDF). Fast Software Encryption 2008. Lecture Notes in Computer Science. Vol. 5086. pp. 16–35. doi:10.1007/978-3-540-71039-4_2. ISBN 978-3-540-71038-7.
- ^ "NIST Brief Comments on Recent Cryptanalytic Attacks on Secure Hashing Functions and the Continued Security Provided by SHA-1". 23 August 2017. Retrieved 2022-03-16.
- ^ Rijmen, Vincent; Oswald, Elisabeth (2005). "Update on SHA-1". Cryptology ePrint Archive.
- ^ Collision Search Attacks on SHA1 Archived 2005-02-19 at the Wayback Machine, Massachusetts Institute of Technology
- ^ Lemos, Robert. "Fixing a hole in security". ZDNet.
- ^ Cochran, Martin (2007). "Notes on the Wang et al. 263 SHA-1 Differential Path". Cryptology ePrint Archive.
- ^ De Cannière, Christophe; Rechberger, Christian (2006-11-15). "Finding SHA-1 Characteristics: General Results and Applications". Advances in Cryptology – ASIACRYPT 2006. Lecture Notes in Computer Science. Vol. 4284. pp. 1–20. doi:10.1007/11935230_1. ISBN 978-3-540-49475-1.
- ^ "IAIK Krypto Group — Description of SHA-1 Collision Search Project". Archived from the original on 2013-01-15. Retrieved 2009-06-30.
- ^ "Collisions for 72-step and 73-step SHA-1: Improvements in the Method of Characteristics". Retrieved 2010-07-24.
- ^ "SHA-1 Collision Search Graz". Archived from the original on 2009-02-25. Retrieved 2009-06-30.
- ^ "heise online – IT-News, Nachrichten und Hintergründe". heise online. 27 August 2023.
- ^ "Crypto 2006 Rump Schedule". www.iacr.org.
- ^ Manuel, Stéphane. "Classification and Generation of Disturbance Vectors for Collision Attacks against SHA-1" (PDF). Cryptology ePrint Archive. Retrieved 2011-05-19.
- ^ Manuel, Stéphane (2011). "Classification and Generation of Disturbance Vectors for Collision Attacks against SHA-1". Designs, Codes and Cryptography. 59 (1–3): 247–263. doi:10.1007/s10623-010-9458-9. S2CID 47179704. the most efficient disturbance vector is Codeword2 first reported by Jutla and Patthak
- ^ "SHA-1 collisions now 2^52" (PDF).
- ^ McDonald, Cameron; Hawkes, Philip; Pieprzyk, Josef (2009). "Differential Path for SHA-1 with complexity O(252)". Cryptology ePrint Archive. (withdrawn)
- ^ "Cryptanalysis of MD5 & SHA-1" (PDF).
- ^ "When Will We See Collisions for SHA-1? – Schneier on Security". www.schneier.com.
- ^ "Google Code Archive – Long-term storage for Google Code Project Hosting". code.google.com.
- ^ Leurent, Gaëtan; Peyrin, Thomas (2019). "From Collisions to Chosen-Prefix Collisions Application to Full SHA-1" (PDF). In Yuval Ishai; Vincent Rijmen (eds.). Advances in Cryptology – EUROCRYPT 2019 (PDF). 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19–23, 2019. Lecture Notes in Computer Science. Vol. 11478. Springer. pp. 527–555. doi:10.1007/978-3-030-17659-4_18. ISBN 978-3-030-17658-7. S2CID 153311244.
- ^ "RFC 3174 - US Secure Hash Algorithm 1 (SHA1) (RFC3174)". www.faqs.org.
- ^ Locktyukhin, Max (2010-03-31), "Improving the Performance of the Secure Hash Algorithm (SHA-1)", Intel Software Knowledge Base, retrieved 2010-04-02
- ^ "Measurements table". bench.cr.yp.to.
- ^ Tao, Xie; Liu, Fanbao; Feng, Dengguo (2013). Fast Collision Attack on MD5 (PDF). Cryptology ePrint Archive (Technical report). IACR.
- ^ Stevens, Marc; Bursztein, Elie; Karpman, Pierre; Albertini, Ange; Markov, Yarik. The first collision for full SHA-1 (PDF) (Technical report). Google Research.
- Marc Stevens; Elie Bursztein; Pierre Karpman; Ange Albertini; Yarik Markov; Alex Petit Bianco; Clement Baisse (February 23, 2017). "Announcing the first SHA1 collision". Google Security Blog.
- ^ Without truncation, the full internal state of the hash function is known, regardless of collision resistance. If the output is truncated, the removed part of the state must be searched for and found before the hash function can be resumed, allowing the attack to proceed.
- ^ "The Keccak sponge function family". Retrieved 2016-01-27.
- ^ IBM z/Architecture Principles of Operation, publication number SA22-7832. See KIMD and KLMD instructions in Chapter 7.
- ^ Stevens, Marc (2017). "cr-marcstevens/sha1collisiondetection: Library and command line tool to detect SHA-1 collision in a file".
- ^ King, Jeff (10 May 2017). "Git 2.13 has been released". The GitHub Blog.
References
[edit]- Eli Biham, Rafi Chen, Near-Collisions of SHA-0, Cryptology ePrint Archive, Report 2004/146, 2004 (appeared on CRYPTO 2004), IACR.org
- Xiaoyun Wang, Hongbo Yu and Yiqun Lisa Yin, Efficient Collision Search Attacks on SHA-0, Crypto 2005
- Xiaoyun Wang, Yiqun Lisa Yin and Hongbo Yu, Finding Collisions in the Full SHA-1, Crypto 2005
- Henri Gilbert, Helena Handschuh: Security Analysis of SHA-256 and Sisters. Selected Areas in Cryptography 2003: pp175–193
- An Illustrated Guide to Cryptographic Hashes
- "Proposed Revision of Federal Information Processing Standard (FIPS) 180, Secure Hash Standard". Federal Register. 59 (131): 35317–35318. 1994-07-11. Retrieved 2007-04-26.[permanent dead link]
- A. Cilardo, L. Esposito, A. Veniero, A. Mazzeo, V. Beltran, E. Ayugadé, A CellBE-based HPC application for the analysis of vulnerabilities in cryptographic hash functions, High Performance Computing and Communication international conference, August 2010
External links
[edit]- CSRC Cryptographic Toolkit – Official NIST site for the Secure Hash Standard
- FIPS 180-4: Secure Hash Standard (SHS)
- RFC 3174 (with sample C implementation)
- Interview with Yiqun Lisa Yin concerning the attack on SHA-1
- Explanation of the successful attacks on SHA-1 (3 pages, 2006)
- Cryptography Research – Hash Collision Q&A
- SHA-1 at Curlie
- Lecture on SHA-1 (1h 18m) on YouTube by Christof Paar Archived 2017-04-24 at the Wayback Machine
| |||||||||||||||||||||||||||||
