
| ||
| oblate | prolate | |
|---|---|---|
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.
If the ellipse is rotated about its major axis, the result is a prolate spheroid, elongated like a rugby ball. The American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an oblate spheroid, flattened like a lentil or a plain M&M. If the generating ellipse is a circle, the result is a sphere.
Due to the combined effects of gravity and rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattened in the direction of its axis of rotation. For that reason, in cartography and geodesy the Earth is often approximated by an oblate spheroid, known as the reference ellipsoid, instead of a sphere. The current World Geodetic System model uses a spheroid whose radius is 6,378.137 km (3,963.191 mi) at the Equator and 6,356.752 km (3,949.903 mi) at the poles.
The word spheroid originally meant "an approximately spherical body", admitting irregularities even beyond the bi- or tri-axial ellipsoidal shape; that is how the term is used in some older papers on geodesy (for example, referring to truncated spherical harmonic expansions of the Earth's gravity geopotential model).[1]
Equation
[edit]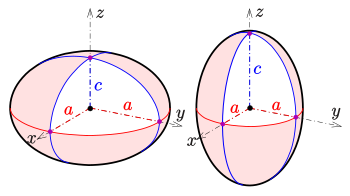
The equation of a tri-axial ellipsoid centred at the origin with semi-axes a, b and c aligned along the coordinate axes is
The equation of a spheroid with z as the symmetry axis is given by setting a = b:
The semi-axis a is the equatorial radius of the spheroid, and c is the distance from centre to pole along the symmetry axis. There are two possible cases:
- c < a: oblate spheroid
- c > a: prolate spheroid
The case of a = c reduces to a sphere.
Properties
[edit]Area
[edit]An oblate spheroid with c < a has surface area
The oblate spheroid is generated by rotation about the z-axis of an ellipse with semi-major axis a and semi-minor axis c, therefore e may be identified as the eccentricity. (See ellipse.)[2]
A prolate spheroid with c > a has surface area
The prolate spheroid is generated by rotation about the z-axis of an ellipse with semi-major axis c and semi-minor axis a; therefore, e may again be identified as the eccentricity. (See ellipse.) [3]
These formulas are identical in the sense that the formula for Soblate can be used to calculate the surface area of a prolate spheroid and vice versa. However, e then becomes imaginary and can no longer directly be identified with the eccentricity. Both of these results may be cast into many other forms using standard mathematical identities and relations between parameters of the ellipse.
Volume
[edit]The volume inside a spheroid (of any kind) is
If A = 2a is the equatorial diameter, and C = 2c is the polar diameter, the volume is
Curvature
[edit]Let a spheroid be parameterized as
where β is the reduced latitude or parametric latitude, λ is the longitude, and −π/2 < β < +π/2 and −π < λ < +π. Then, the spheroid's Gaussian curvature is
and its mean curvature is
Both of these curvatures are always positive, so that every point on a spheroid is elliptic.
Aspect ratio
[edit]The aspect ratio of an oblate spheroid/ellipse, c : a, is the ratio of the polar to equatorial lengths, while the flattening (also called oblateness) f, is the ratio of the equatorial-polar length difference to the equatorial length:
The first eccentricity (usually simply eccentricity, as above) is often used instead of flattening.[4] It is defined by:
The relations between eccentricity and flattening are:
All modern geodetic ellipsoids are defined by the semi-major axis plus either the semi-minor axis (giving the aspect ratio), the flattening, or the first eccentricity. While these definitions are mathematically interchangeable, real-world calculations must lose some precision. To avoid confusion, an ellipsoidal definition considers its own values to be exact in the form it gives.
Occurrence and applications
[edit]The most common shapes for the density distribution of protons and neutrons in an atomic nucleus are spherical, prolate, and oblate spheroidal, where the polar axis is assumed to be the spin axis (or direction of the spin angular momentum vector). Deformed nuclear shapes occur as a result of the competition between electromagnetic repulsion between protons, surface tension and quantum shell effects.
Spheroids are common in 3D cell cultures. Rotating equilibrium spheroids include the Maclaurin spheroid and the Jacobi ellipsoid. Spheroid is also a shape of archaeological artifacts.
Oblate spheroids
[edit]
The oblate spheroid is the approximate shape of rotating planets and other celestial bodies, including Earth, Saturn, Jupiter, and the quickly spinning star Altair. Saturn is the most oblate planet in the Solar System, with a flattening of 0.09796. See planetary flattening and equatorial bulge for details.
Enlightenment scientist Isaac Newton, working from Jean Richer's pendulum experiments and Christiaan Huygens's theories for their interpretation, reasoned that Jupiter and Earth are oblate spheroids owing to their centrifugal force.[5][6] Earth's diverse cartographic and geodetic systems are based on reference ellipsoids, all of which are oblate.
Prolate spheroids
[edit]
The prolate spheroid is the approximate shape of the ball in several sports, such as in the rugby ball.
Several moons of the Solar System approximate prolate spheroids in shape, though they are actually triaxial ellipsoids. Examples are Saturn's satellites Mimas, Enceladus, and Tethys and Uranus' satellite Miranda.
In contrast to being distorted into oblate spheroids via rapid rotation, celestial objects distort slightly into prolate spheroids via tidal forces when they orbit a massive body in a close orbit. The most extreme example is Jupiter's moon Io, which becomes slightly more or less prolate in its orbit due to a slight eccentricity, causing intense volcanism. The major axis of the prolate spheroid does not run through the satellite's poles in this case, but through the two points on its equator directly facing toward and away from the primary. This combines with the smaller oblate distortion from the synchronous rotation to cause the body to become triaxial.
The term is also used to describe the shape of some nebulae such as the Crab Nebula.[7] Fresnel zones, used to analyze wave propagation and interference in space, are a series of concentric prolate spheroids with principal axes aligned along the direct line-of-sight between a transmitter and a receiver.
The atomic nuclei of the actinide and lanthanide elements are shaped like prolate spheroids.[8] In anatomy, near-spheroid organs such as testis may be measured by their long and short axes.[9]
Many submarines have a shape which can be described as prolate spheroid.[10]
Dynamical properties
[edit]For a spheroid having uniform density, the moment of inertia is that of an ellipsoid with an additional axis of symmetry. Given a description of a spheroid as having a major axis c, and minor axes a = b, the moments of inertia along these principal axes are C, A, and B. However, in a spheroid the minor axes are symmetrical. Therefore, our inertial terms along the major axes are:[11]
where M is the mass of the body defined as
See also
[edit]- Ellipsoidal dome
- Equatorial bulge
- Great ellipse
- Lentoid
- Oblate spheroidal coordinates
- Ovoid
- Prolate spheroidal coordinates
- Rotation of axes
- Translation of axes
References
[edit]- ^ Torge, Wolfgang (2001). Geodesy (3rd ed.). Walter de Gruyter. p. 104. ISBN 9783110170726.
- ^ A derivation of this result may be found at "Oblate Spheroid - from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 24 June 2014.
- ^ A derivation of this result may be found at "Prolate Spheroid - from Wolfram MathWorld". Mathworld.wolfram.com. 7 October 2003. Retrieved 24 June 2014.
- ^ Brial P., Shaalan C.(2009), Introduction à la Géodésie et au geopositionnement par satellites, p.8
- ^ Greenburg, John L. (1995). "Isaac Newton and the Problem of the Earth's Shape". History of Exact Sciences. 49 (4). Springer: 371–391. doi:10.1007/BF00374704. JSTOR 41134011. S2CID 121268606.
- ^ Durant, Will; Durant, Ariel (28 July 1997). The Story of Civilization: The Age of Louis XIV. MJF Books. ISBN 1567310192.
- ^ Trimble, Virginia Louise (October 1973), "The Distance to the Crab Nebula and NP 0532", Publications of the Astronomical Society of the Pacific, 85 (507): 579, Bibcode:1973PASP...85..579T, doi:10.1086/129507
- ^ "Nuclear fission - Fission theory". Encyclopedia Britannica.
- ^ Page 559 in: John Pellerito, Joseph F Polak (2012). Introduction to Vascular Ultrasonography (6 ed.). Elsevier Health Sciences. ISBN 9781455737666.
- ^ "What Do a Submarine, a Rocket and a Football Have in Common?". Scientific American. 8 November 2010. Retrieved 13 June 2015.
- ^ Weisstein, Eric W. "Spheroid". MathWorld--A Wolfram Web Resource. Retrieved 16 May 2018.
External links
[edit] Media related to Spheroids at Wikimedia Commons
Media related to Spheroids at Wikimedia Commons- . Encyclopædia Britannica (11th ed.). 1911.













