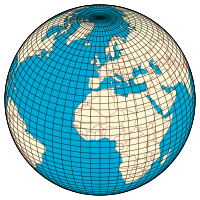
 |
| Longitude (λ) |
|---|
| Lines of longitude appear vertical with varying curvature in this projection, but are actually halves of great ellipses, with identical radii at a given latitude. |
| Latitude (φ) |
| Lines of latitude appear horizontal with varying curvature in this projection; but are actually circular with different radii. All locations with a given latitude are collectively referred to as a circle of latitude. |
|
|
| Geodesy |
|---|
 |
Longitude (/ˈlɒndʒɪtjuːd/, AU and UK also /ˈlɒŋɡɪ-/)[1][2] is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are imaginary semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, south-east London on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west.
Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of time allows longitude to be determined. Depending on the era, the absolute time might be obtained from a celestial event visible from both locations, such as a lunar eclipse, or from a time signal transmitted by telegraph or radio. The principle is straightforward, but in practice finding a reliable method of determining longitude took centuries and required the effort of some of the greatest scientific minds.
A location's north–south position along a meridian is given by its latitude, which is approximately the angle between the equatorial plane and the normal from the ground at that location.
Longitude is generally given using the geodetic normal or the gravity direction. The astronomical longitude can differ slightly from the ordinary longitude because of vertical deflection, small variations in Earth's gravitational field (see astronomical latitude).
History
[edit]The concept of longitude was first developed by ancient Greek astronomers. Hipparchus (2nd century BCE) used a coordinate system that assumed a spherical Earth, and divided it into 360° as we still do today. His prime meridian passed through Alexandria.[3]: 31 He also proposed a method of determining longitude by comparing the local time of a lunar eclipse at two different places, thus demonstrating an understanding of the relationship between longitude and time.[3]: 11 [4] Claudius Ptolemy (2nd century CE) developed a mapping system using curved parallels that reduced distortion. He also collected data for many locations, from Britain to the Middle East. He used a prime meridian through the Canary Islands, so that all longitude values would be positive. While Ptolemy's system was sound, the data he used were often poor, leading to a gross over-estimate (by about 70%) of the length of the Mediterranean.[5][6]: 551–553 [7]
After the fall of the Roman Empire, interest in geography greatly declined in Europe.[8]: 65 Hindu and Muslim astronomers continued to develop these ideas, adding many new locations and often improving on Ptolemy's data.[9][10] For example al-Battānī used simultaneous observations of two lunar eclipses to determine the difference in longitude between Antakya and Raqqa with an error of less than 1°. This is considered to be the best that can be achieved with the methods then available: observation of the eclipse with the naked eye, and determination of local time using an astrolabe to measure the altitude of a suitable "clock star".[11][12]
In the later Middle Ages, interest in geography revived in the west, as travel increased, and Arab scholarship began to be known through contact with Spain and North Africa. In the 12th century, astronomical tables were prepared for a number of European cities, based on the work of al-Zarqālī in Toledo. The lunar eclipse of September 12, 1178 was used to establish the longitude differences between Toledo, Marseilles, and Hereford.[13]: 85
Christopher Columbus made two attempts to use lunar eclipses to discover his longitude, the first in Saona Island, on 14 September 1494 (second voyage), and the second in Jamaica on 29 February 1504 (fourth voyage). It is assumed that he used astronomical tables for reference. His determinations of longitude showed large errors of 13° and 38° W respectively.[14] Randles (1985) documents longitude measurement by the Portuguese and Spanish between 1514 and 1627 both in the Americas and Asia. Errors ranged from 2° to 25°.[15]
The telescope was invented in the early 17th century. Initially an observation device, developments over the next half century transformed it into an accurate measurement tool.[16][17] The pendulum clock was patented by Christiaan Huygens in 1657[18] and gave an increase in accuracy of about 30 fold over previous mechanical clocks.[19] These two inventions would revolutionise observational astronomy and cartography.[20]
On land, the period from the development of telescopes and pendulum clocks until the mid-18th century saw a steady increase in the number of places whose longitude had been determined with reasonable accuracy, often with errors of less than a degree, and nearly always within 2° to 3°. By the 1720s errors were consistently less than 1°.[21] At sea during the same period, the situation was very different. Two problems proved intractable. The first was the need of a navigator for immediate results. The second was the marine environment. Making accurate observations in an ocean swell is much harder than on land, and pendulum clocks do not work well in these conditions.
The chronometer
[edit]
In response to the problems of navigation, a number of European maritime powers offered prizes for a method to determine longitude at sea. The best-known of these is the Longitude Act passed by the British parliament in 1714.[22]: 8 It offered two levels of rewards, for solutions within 1° and 0.5°. Rewards were given for two solutions: lunar distances, made practicable by the tables of Tobias Mayer[23] developed into an nautical almanac by the Astronomer Royal Nevil Maskelyne; and for the chronometers developed by the Yorkshire carpenter and clock-maker John Harrison. Harrison built five chronometers over more than three decades. This work was supported and rewarded with thousands of pounds from the Board of Longitude,[24] but he fought to receive money up to the top reward of £20,000, finally receiving an additional payment in 1773 after the intervention of parliament.[22]: 26 It was some while before either method became widely used in navigation. In the early years, chronometers were very expensive, and the calculations required for lunar distances were still complex and time-consuming. Lunar distances came into general use after 1790.[25] Chronometers had the advantages that both the observations and the calculations were simpler, and as they became cheaper in the early 19th century they started to replace lunars, which were seldom used after 1850.[26]
The first working telegraphs were established in Britain by Wheatstone and Cooke in 1839, and in the US by Morse in 1844. It was quickly realised that the telegraph could be used to transmit a time signal for longitude determination.[27] The method was soon in practical use for longitude determination, especially in North America, and over longer and longer distances as the telegraph network expanded, including western Europe with the completion of transatlantic cables. The United States Coast Survey, renamed the United States Coast and Geodetic Survey in 1878, was particularly active in this development, and not just in the United States. The Survey established chains of mapped locations through Central and South America, and the West Indies, and as far as Japan and China in the years 1874–90. This contributed greatly to the accurate mapping of these areas.[28][29]
While mariners benefited from the accurate charts, they could not receive telegraph signals while under way, and so could not use the method for navigation. This changed when wireless telegraphy (radio) became available in the early 20th century.[30] Wireless time signals for the use of ships were transmitted from Halifax, Nova Scotia, starting in 1907[31] and from the Eiffel Tower in Paris from 1910.[32] These signals allowed navigators to check and adjust their chronometers frequently.[33]
Radio navigation systems came into general use after World War II. The systems all depended on transmissions from fixed navigational beacons. A ship-board receiver calculated the vessel's position from these transmissions.[34] They allowed accurate navigation when poor visibility prevented astronomical observations, and became the established method for commercial shipping until replaced by GPS in the early 1990s.
Determination
[edit]The main methods for determining longitude are listed below. With one exception (magnetic declination) they all depend on a common principle, which was to determine an absolute time from an event or measurement and to compare the corresponding local time at two different locations.
- Lunar distances. In its orbit around the Earth, the Moon moves relative to the stars at a rate of just over 0.5°/hour. The angle between the Moon and a suitable star is measured with a sextant, and (after consulting tables and lengthy calculations) gives a value for absolute time.
- Satellites of Jupiter. Galileo proposed that with sufficiently accurate knowledge of the orbits of the satellites, their positions could provide a measure of absolute time. The method requires a telescope, as the moons are not visible to the naked eye.
- Appulses, occultations, and eclipses. An appulse is the least apparent distance between two objects (the Moon, a star or a planet); an occultation occurs when a star or planet passes behind the Moon — essentially a type of eclipse. Lunar eclipses continued to be used. The times of any of these events can be used as the measure of absolute time.
- Chronometers. A clock is set to the local time of a starting point whose longitude is known, and the longitude of any other place can be determined by comparing its local time with the clock time.
- Magnetic declination. A compass needle does not in general point exactly north. The variation from true north varies with location, and it was suggested that this could provide a basis for determination of longitude.
With the exception of magnetic declination, all proved practicable methods. Developments on land and sea, however, were very different.
Longitude at a point may be determined by calculating the time difference between that at its location and Coordinated Universal Time (UTC). Since there are 24 hours in a day and 360 degrees in a circle, the sun moves across the sky at a rate of 15 degrees per hour (360° ÷ 24 hours = 15° per hour). So if a location's time zone is three hours ahead of UTC then that location is near 45° longitude (3 hours × 15° per hour = 45°). The word near is used because the point might not be at the centre of the time zone; also the time zones are defined politically, so their centres and boundaries often do not lie on meridians at multiples of 15°. In order to perform this calculation, however, one needs a chronometer (watch) set to UTC and needs to determine local time by solar or astronomical observation. The details are more complex than described here: see the articles on Universal Time and on the equation of time for more details.
Values
[edit]Longitude is given as an angular measurement with 0° at the Prime Meridian, ranging from −180° westward to +180° eastward. The Greek letter λ (lambda)[35][36] is used to denote the location of a place on Earth east or west of the Prime Meridian.
Each degree of longitude is sub-divided into 60 minutes, each of which is divided into 60 seconds. A longitude is thus specified in sexagesimal notation as, for example, 23° 27′ 30″ E. For higher precision, the seconds are specified with a decimal fraction. An alternative representation uses degrees and minutes, and parts of a minute are expressed in decimal notation, thus: 23° 27.5′ E. Degrees may also be expressed as a decimal fraction: 23.45833° E. For calculations, the angular measure may be converted to radians, so longitude may also be expressed in this manner as a signed fraction of π (pi), or an unsigned fraction of 2π.
For calculations, the West/East suffix is replaced by a negative sign in the western hemisphere. The international standard convention (ISO 6709)—that East is positive—is consistent with a right-handed Cartesian coordinate system, with the North Pole up. A specific longitude may then be combined with a specific latitude (positive in the northern hemisphere) to give a precise position on the Earth's surface. Confusingly, the convention of negative for East is also sometimes seen, most commonly in the United States; the Earth System Research Laboratories used it on an older version of one of their pages, in order "to make coordinate entry less awkward" for applications confined to the Western Hemisphere. They have since shifted to the standard approach.[37]
The longitude is singular at the Poles and calculations that are sufficiently accurate for other positions may be inaccurate at or near the Poles. Also the discontinuity at the ±180° meridian must be handled with care in calculations. An example is a calculation of east displacement by subtracting two longitudes, which gives the wrong answer if the two positions are on either side of this meridian. To avoid these complexities, some applications use another horizontal position representation.
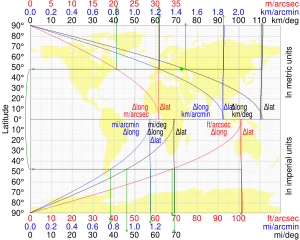
Length of a degree of longitude
[edit]The length of a degree of longitude (east–west distance) depends only on the radius of a circle of latitude. For a sphere of radius a that radius at latitude φ is a cos φ, and the length of a one-degree (or π/180 radian) arc along a circle of latitude is
| φ | Δ1 lat |
Δ1 long |
|---|---|---|
| 0° | 110.574 km | 111.320 km |
| 15° | 110.649 km | 107.551 km |
| 30° | 110.852 km | 96.486 km |
| 45° | 111.133 km | 78.847 km |
| 60° | 111.412 km | 55.800 km |
| 75° | 111.618 km | 28.902 km |
| 90° | 111.694 km | 0.000 km |
When the Earth is modelled by an ellipsoid this arc length becomes[38][39]
where e, the eccentricity of the ellipsoid, is related to the major and minor axes (the equatorial and polar radii respectively) by
An alternative formula is
- ; here is the so-called parametric or reduced latitude.
cos φ decreases from 1 at the equator to 0 at the poles, which measures how circles of latitude shrink from the equator to a point at the pole, so the length of a degree of longitude decreases likewise. This contrasts with the small (1%) increase in the length of a degree of latitude (north–south distance), equator to pole. The table shows both for the WGS84 ellipsoid with a = 6378137.0 m and b = 6356752.3142 m. The distance between two points 1 degree apart on the same circle of latitude, measured along that circle of latitude, is slightly more than the shortest (geodesic) distance between those points (unless on the equator, where these are equal); the difference is less than 0.6 m (2 ft).
A geographical mile is defined to be the length of one minute of arc along the equator (one equatorial minute of longitude) therefore a degree of longitude along the equator is exactly 60 geographical miles or 111.3 kilometers, as there are 60 minutes in a degree. The length of 1 minute of longitude along the equator is 1 geographical mile or 1.855 km or 1.153 miles, while the length of 1 second of it is 0.016 geographical mile or 30.916 m or 101.43 feet.
See also
[edit]- American Practical Navigator
- Cardinal direction
- Dead reckoning
- Ecliptic longitude
- Geodesy
- Geodetic system
- Geographic coordinate system
- Geographical distance
- Geotagging
- Great-circle distance
- History of longitude
- The Island of the Day Before
- Latitude
- Meridian arc
- Natural Area Code
- Navigation
- Orders of magnitude
- Planetary coordinate system#Longitude
- Right ascension on celestial sphere
- World Geodetic System
References
[edit]- ^ "Definition of LONGITUDE". Merriam-Webster. Archived from the original on 16 June 2018. Retrieved 14 March 2018.
- ^ Oxford English Dictionary
- ^ a b Dicks, D.R. (1953). Hipparchus : a critical edition of the extant material for his life and works (PhD). Birkbeck College, University of London. Archived from the original on 2021-04-14. Retrieved 2020-09-26.
- ^ Hoffman, Susanne M. (2016). "How time served to measure the geographical position since Hellenism". In Arias, Elisa Felicitas; Combrinck, Ludwig; Gabor, Pavel; Hohenkerk, Catherine; Seidelmann, P.Kenneth (eds.). The Science of Time. Astrophysics and Space Science Proceedings. Vol. 50. Springer International. pp. 25–36. doi:10.1007/978-3-319-59909-0_4. ISBN 978-3-319-59908-3.
- ^ Mittenhuber, Florian (2010). "The Tradition of Texts and Maps in Ptolemy's Geography". In Jones, Alexander (ed.). Ptolemy in Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century. Archimedes. Vol. 23. Dordrecht: Springer. pp. 95-119. doi:10.1007/978-90-481-2788-7_4. ISBN 978-90-481-2787-0.
- ^ Bunbury, E.H. (1879). A History of Ancient Geography. Vol. 2. London: John Murray.
- ^ Shcheglov, Dmitry A. (2016). "The Error in Longitude in Ptolemy's Geography Revisited". The Cartographic Journal. 53 (1): 3–14. Bibcode:2016CartJ..53....3S. doi:10.1179/1743277414Y.0000000098. S2CID 129864284.
- ^ Wright, John Kirtland (1925). The geographical lore of the time of the Crusades: A study in the history of medieval science and tradition in Western Europe. New York: American geographical society.
- ^ Ragep, F.Jamil (2010). "Islamic reactions to Ptolemy's imprecisions". In Jones, A. (ed.). Ptolemy in Perspective. Archimedes. Vol. 23. Dordrecht: Springer. doi:10.1007/978-90-481-2788-7. ISBN 978-90-481-2788-7. Archived from the original on 2022-07-07. Retrieved 2022-03-23.
- ^ Tibbetts, Gerald R. (1992). "The Beginnings of a Cartographic Tradition" (PDF). In Harley, J.B.; Woodward, David (eds.). The History of Cartography Vol. 2 Cartography in the Traditional Islamic and South Asian Societies. University of Chicago Press. Archived (PDF) from the original on 2020-09-21. Retrieved 2020-09-26.
- ^ Said, S.S.; Stevenson, F.R. (1997). "Solar and Lunar Eclipse Measurements by Medieval Muslim Astronomers, II: Observations". Journal for the History of Astronomy. 28 (1): 29–48. Bibcode:1997JHA....28...29S. doi:10.1177/002182869702800103. S2CID 117100760.
- ^ Steele, John Michael (1998). Observations and predictions of eclipse times by astronomers in the pre-telescopic period (PhD). University of Durham (United Kingdom).
- ^ Wright, John Kirtland (1923). "Notes on the Knowledge of Latitudes and Longitudes in the Middle Ages". Isis. 5 (1). Bibcode:1922nkll.book.....W.
- ^ Pickering, Keith (1996). "Columbus's Method of Determining Longitude: An Analytical View". The Journal of Navigation. 49 (1): 96–111. Bibcode:1996JNav...49...95P. doi:10.1017/S037346330001314X. S2CID 129232861.
- ^ Randles, W.G.L. (1985). "Portuguese and Spanish attempts to measure longitude in the 16th century". Vistas in Astronomy. 28 (1): 235–241. Bibcode:1985VA.....28..235R. doi:10.1016/0083-6656(85)90031-5.
- ^ Pannekoek, Anton (1989). A history of astronomy. Courier Corporation. pp. 259–276.
- ^ Van Helden, Albert (1974). "The Telescope in the Seventeenth Century". Isis. 65 (1): 38–58. doi:10.1086/351216. JSTOR 228880. S2CID 224838258.
- ^ Grimbergen, Kees (2004). Fletcher, Karen (ed.). Huygens and the advancement of time measurements. Titan - From Discovery to Encounter. Titan - from Discovery to Encounter. Vol. 1278. ESTEC, Noordwijk, Netherlands: ESA Publications Division. pp. 91–102. Bibcode:2004ESASP1278...91G. ISBN 92-9092-997-9.
- ^ Blumenthal, Aaron S.; Nosonovsky, Michael (2020). "Friction and Dynamics of Verge and Foliot: How the Invention of the Pendulum Made Clocks Much More Accurate". Applied Mechanics. 1 (2): 111–122. doi:10.3390/applmech1020008.
- ^ Olmsted, J.W. (1960). "The Voyage of Jean Richer to Acadia in 1670: A Study in the Relations of Science and Navigation under Colbert". Proceedings of the American Philosophical Society. 104 (6): 612–634. JSTOR 985537.
- ^ See, for example, Port Royal, Jamaica: Halley, Edmond (1722). "Observations on the Eclipse of the Moon, June 18, 1722. and the Longitude of Port Royal in Jamaica". Philosophical Transactions. 32 (370–380): 235–236.; Buenos Aires: Halley, Edm. (1722). "The Longitude of Buenos Aires, Determin'd from an Observation Made There by Père Feuillée". Philosophical Transactions. 32 (370–380): 2–4.Santa Catarina, Brazil: Legge, Edward; Atwell, Joseph (1743). "Extract of a letter from the Honble Edward Legge, Esq; F. R. S. Captain of his Majesty's ship the Severn, containing an observation of the eclipse of the moon, Dec. 21. 1740. at the Island of St. Catharine on the Coast of Brasil". Philosophical Transactions. 42 (462): 18–19.
- ^ a b Siegel, Jonathan R. (2009). "Law and Longitude". Tulane Law Review. 84: 1–66.
- ^ Forbes, Eric Gray (2006). "Tobias Mayer's lunar tables". Annals of Science. 22 (2): 105–116. doi:10.1080/00033796600203075. ISSN 0003-3790.
- ^ "There was no such thing as the Longitude Prize". Royal Museums Greenwich. 2012-03-07. Archived from the original on 2023-01-22. Retrieved 2021-01-27.
- ^ Wess, Jane (2015). "Navigation and Mathematics: A Match Made in the Heavens?". In Dunn, Richard; Higgitt, Rebekah (eds.). Navigational Enterprises in Europe and its Empires, 1730-1850. London: Palgrave Macmillan UK. pp. 201–222. doi:10.1057/9781137520647_11. ISBN 978-1-349-56744-7.
- ^ Littlehales, G.W. (1909). "The Decline of the Lunar Distance for the Determination of the Time and Longitude at". Bulletin of the American Geographical Society. 41 (2): 83–86. doi:10.2307/200792. JSTOR 200792.
- ^ Walker, Sears C (1850). "Report on the experience of the Coast Survey in regard to telegraph operations, for determination of longitude &c". American Journal of Science and Arts. 10 (28): 151–160.
- ^ Knox, Robert W. (1957). "Precise Determination of Longitude in the United States". Geographical Review. 47 (4): 555–563. Bibcode:1957GeoRv..47..555K. doi:10.2307/211865. JSTOR 211865.
- ^ Green, Francis Mathews; Davis, Charles Henry; Norris, John Alexander (1883). Telegraphic Determination of Longitudes in Japan, China, and the East Indies: Embracing the Meridians of Yokohama, Nagasaki, Wladiwostok, Shanghai, Amoy, Hong-Kong, Manila, Cape St. James, Singapore, Batavia, and Madras, with the Latitude of the Several Stations. Washington: US Hydrographic Office.
- ^ Munro, John (1902). "Time-Signals by Wireless Telegraphy". Nature. 66 (1713): 416. Bibcode:1902Natur..66..416M. doi:10.1038/066416d0. ISSN 0028-0836. S2CID 4021629. Archived from the original on 2021-04-14. Retrieved 2020-09-26.
- ^ Hutchinson, D.L. (1908). "Wireless Time Signals from the St. John Observatory of the Canadian Meteorological Service". Proceedings and Transactions of the Royal Society of Canada. Ser. 3 Vol. 2: 153–154.
- ^ Lockyer, William J. S. (1913). "International Time and Weather Radio-Telegraphic Signals". Nature. 91 (2263): 33–36. Bibcode:1913Natur..91...33L. doi:10.1038/091033b0. ISSN 0028-0836. S2CID 3977506.
- ^ Zimmerman, Arthur E. "The first wireless time signals to ships at sea" (PDF). antiquewireless.org. Antique Wireless Association. Archived (PDF) from the original on 11 July 2020. Retrieved 9 July 2020.
- ^ Pierce, J.A. (1946). "An introduction to Loran". Proceedings of the IRE. 34 (5): 216–234. doi:10.1109/JRPROC.1946.234564. S2CID 20739091.
- ^ "Coordinate Conversion". colorado.edu. Archived from the original on 29 September 2009. Retrieved 14 March 2018.
- ^ "λ = Longitude east of Greenwich (for longitude west of Greenwich, use a minus sign)."
John P. Snyder, Map Projections, A Working Manual Archived 2010-07-01 at the Wayback Machine, USGS Professional Paper 1395, page ix - ^ NOAA ESRL Sunrise/Sunset Calculator Archived 2019-10-31 at the Wayback Machine (deprecated). Earth System Research Laboratories. Retrieved October 18, 2019.
- ^ Osborne, Peter (2013). "Chapter 5: The geometry of the ellipsoid". The Mercator Projections: The Normal and Transverse Mercator Projections on the Sphere and the Ellipsoid with Full Derivations of all Formulae (PDF). Edinburgh. doi:10.5281/zenodo.35392. Archived from the original (PDF) on 2016-05-09. Retrieved 2016-01-24.
((cite book)): CS1 maint: location missing publisher (link) - ^ Rapp, Richard H. (April 1991). "Chapter 3: Properties of the Ellipsoid". Geometric Geodesy Part I. Columbus, Ohio.: Department of Geodetic Science and Surveying, Ohio State University. hdl:1811/24333.
Further reading
[edit]- Andrews, William J. H. (1996). The Quest for Longitude. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-9644329-0-1. OCLC 59617314.
- Howse, Derek (1980). Greenwich Time and the Discovery of the Longitude. Philip Wilson Publishers, Ltd. ISBN 978-0-19-215948-9.
External links
[edit]- Resources for determining your latitude and longitude Archived 2008-05-19 at the Wayback Machine
- IAU/IAG Working Group On Cartographic Coordinates and Rotational Elements of the Planets and Satellites Archived 2006-04-06 at the Wayback Machine
- "Longitude forged": an essay exposing a hoax solution to the problem of calculating longitude, undetected in Dava Sobel's Longitude, from TLS, November 12, 2008.
- Board of Longitude Collection, Cambridge Digital Library – complete digital version of the Board's archive
- Longitude And Latitude Of Points of Interest
- Length Of A Degree Of Latitude And Longitude Calculator
- Esame critico intorno alla scoperta di Vespucci ...
- A land beyond the stars - Museo Galileo
| Longwave | |
|---|---|
| Shortwave | |
| VHF/FM/UHF | |
| Satellite | |
| Defunct | |
| Key concepts | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Measurement and standards |
| ||||||||
| Philosophy of time | |||||||||
| |||||||||
| Human experience and use of time | |||||||||
| Time in science |
| ||||||||
| Related | |||||||||
| International standards |
| |
|---|---|---|
| Obsolete standards | ||
| Time in physics | ||
| Horology | ||
| Calendar | ||
| Archaeology and geology | ||
| Astronomical chronology | ||
| Other units of time | ||
| Related topics | ||







