In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, which may be centered on Earth or the observer. If centered on the observer, half of the sphere would resemble a hemispherical screen over the observing location.
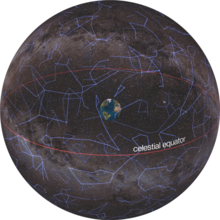
The celestial sphere is a conceptual tool used in spherical astronomy to specify the position of an object in the sky without consideration of its linear distance from the observer. The celestial equator divides the celestial sphere into northern and southern hemispheres.
Because astronomical objects are at such remote distances, casual observation of the sky offers no information on their actual distances. All celestial objects seem equally far away, as if fixed onto the inside of a sphere with a large but unknown radius,[1] which appears to rotate westward overhead; meanwhile, Earth underfoot seems to remain still. For purposes of spherical astronomy, which is concerned only with the directions to celestial objects, it makes no difference if this is actually the case or if it is Earth that is rotating while the celestial sphere is stationary.
The celestial sphere can be considered to be infinite in radius. This means any point within it, including that occupied by the observer, can be considered the center. It also means that all parallel lines, be they millimetres apart or across the Solar System from each other, will seem to intersect the sphere at a single point, analogous to the vanishing point of graphical perspective.[2] All parallel planes will seem to intersect the sphere in a coincident great circle[3] (a "vanishing circle").
Conversely, observers looking toward the same point on an infinite-radius celestial sphere will be looking along parallel lines, and observers looking toward the same great circle, along parallel planes. On an infinite-radius celestial sphere, all observers see the same things in the same direction.
For some objects, this is over-simplified. Objects which are relatively near to the observer (for instance, the Moon) will seem to change position against the distant celestial sphere if the observer moves far enough, say, from one side of planet Earth to the other. This effect, known as parallax, can be represented as a small offset from a mean position. The celestial sphere can be considered to be centered at the Earth's center, the Sun's center, or any other convenient location, and offsets from positions referred to these centers can be calculated.[4]
In this way, astronomers can predict geocentric or heliocentric positions of objects on the celestial sphere, without the need to calculate the individual geometry of any particular observer, and the utility of the celestial sphere is maintained. Individual observers can work out their own small offsets from the mean positions, if necessary. In many cases in astronomy, the offsets are insignificant.
The celestial sphere can thus be thought of as a kind of astronomical shorthand, and is applied very frequently by astronomers. For instance, the Astronomical Almanac for 2010 lists the apparent geocentric position of the Moon on January 1 at 00:00:00.00 Terrestrial Time, in equatorial coordinates, as right ascension 6h 57m 48.86s, declination +23° 30' 05.5". Implied in this position is that it is as projected onto the celestial sphere; any observer at any location looking in that direction would see the "geocentric Moon" in the same place against the stars. For many rough uses (e.g. calculating an approximate phase of the Moon), this position, as seen from the Earth's center, is adequate.
For applications requiring precision (e.g. calculating the shadow path of an eclipse), the Almanac gives formulae and methods for calculating the topocentric coordinates, that is, as seen from a particular place on the Earth's surface, based on the geocentric position.[5] This greatly abbreviates the amount of detail necessary in such almanacs, as each observer can handle their own specific circumstances.
Celestial spheres (or celestial orbs) were envisioned to be perfect and divine entities initially from Greek astronomers such as Aristotle. He composed a set of principles called Aristotelian physics that outlined the natural order and structure of the world. Like other Greek astronomers, Aristotle also thought the "...celestial sphere as the frame of reference for their geometric theories of the motions of the heavenly bodies".[6] With his adoption of Eudoxus of Cnidus' theory, Aristotle had described celestial bodies within the Celestial sphere to be filled with pureness, perfect and quintessence (the fifth element that was known to be divine and purity according to Aristotle). Aristotle deemed the Sun, Moon, planets and the fixed stars to be perfectly concentric spheres in a superlunary region above the sublunary sphere. Aristotle had asserted that these bodies (in the superlunary region) are perfect and cannot be corrupted by any of the classical elements: fire, water, air, and earth. Corruptible elements were only contained in the sublunary region and incorruptible elements were in the superlunary region of Aristotle's geocentric model. Aristotle had the notion that celestial orbs must exhibit celestial motion (a perfect circular motion) that goes on for eternity. He also argued that the behavior and property follows strictly to a principle of natural place where the quintessential element moves freely of divine will, while other elements, fire, air, water and earth, are corruptible, subject to change and imperfection. Aristotle's key concepts rely on the nature of the five elements distinguishing the Earth and the Heavens in the astronomical reality, taking Eudoxus's model of separate spheres.
Numerous discoveries from Aristotle and Eudoxus (approximately 395 B.C. to 337 B.C.) have sparked differences in both of their models and sharing similar properties simultaneously. Aristotle and Eudoxus claimed two different counts of spheres in the heavens. According to Eudoxus, there were only 27 spheres in the heavens, while there are 55 spheres in Aristotle's model. Eudoxus attempted to construct his model mathematically from a treatise known as On Speeds (Greek: Περί Ταχών) and asserted the shape of the hippopede or lemniscate was associated with planetary retrogression. Aristotle emphasized that the speed of the celestial orbs is unchanging, like the heavens, while Eudoxus emphasized that the orbs are in a perfect geometrical shape. Eudoxus's spheres would produce undesirable motions to the lower region of the planets, while Aristotle introduced unrollers between each set of active spheres to counteract the motions of the outer set, or else the outer motions will be transferred to the outer planets. Aristotle would later observe "...the motions of the planets by using the combinations of nested spheres and circular motions in creative ways, but further observations kept undoing their work".[7]
Aside from Aristotle and Eudoxus, Empedocles gave an explanation that the motion of the heavens, moving about it at divine (relatively high) speed, puts the Earth in a stationary position due to the circular motion preventing the downward movement from natural causes. Aristotle criticized Empedocles's model, arguing that all heavy objects go towards the Earth and not the whirl itself coming to Earth. He ridiculed it and claimed that Empedocles's statement was extremely absurd. Anything that defied the motion of natural place and the unchanging heavens (including the celestial spheres) was criticized immediately by Aristotle.
These concepts are important for understanding celestial coordinate systems, frameworks for measuring the positions of objects in the sky. Certain reference lines and planes on Earth, when projected onto the celestial sphere, form the bases of the reference systems. These include the Earth's equator, axis, and orbit. At their intersections with the celestial sphere, these form the celestial equator, the north and south celestial poles, and the ecliptic, respectively.[8] As the celestial sphere is considered arbitrary or infinite in radius, all observers see the celestial equator, celestial poles, and ecliptic at the same place against the background stars.
From these bases, directions toward objects in the sky can be quantified by constructing celestial coordinate systems. Similar to geographic longitude and latitude, the equatorial coordinate system specifies positions relative to the celestial equator and celestial poles, using right ascension and declination. The ecliptic coordinate system specifies positions relative to the ecliptic (Earth's orbit), using ecliptic longitude and latitude. Besides the equatorial and ecliptic systems, some other celestial coordinate systems, like the galactic coordinate system, are more appropriate for particular purposes.
|
Main article: Cosmic pluralism |
|
Further information: History of astronomy |
The ancients assumed the literal truth of stars attached to a celestial sphere, revolving about the Earth in one day, and a fixed Earth.[9] The Eudoxan planetary model, on which the Aristotelian and Ptolemaic models were based, was the first geometric explanation for the "wandering" of the classical planets.[10] The outermost of these "crystal spheres" was thought to carry the fixed stars. Eudoxus used 27 concentric spherical solids to answer Plato's challenge: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?"[11] Anaxagoras in the mid 5th century BC was the first known philosopher to suggest that the stars were "fiery stones" too far away for their heat to be felt. Similar ideas were expressed by Aristarchus of Samos. However, they did not enter mainstream astronomy of the late ancient and medieval period. Copernican heliocentrism did away with the planetary spheres, but it did not necessarily preclude the existence of a sphere for the fixed stars. The first astronomer of the European Renaissance to suggest that the stars were distant suns was Giordano Bruno in his De l'infinito universo et mondi (1584). This idea was among the charges, albeit not in a prominent position, brought against him by the Inquisition. The idea became mainstream in the later 17th century, especially following the publication of Conversations on the Plurality of Worlds by Bernard Le Bovier de Fontenelle (1686), and by the early 18th century it was the default working assumptions in stellar astronomy.

|
Main articles: Star chart, Armillary sphere, and Celestial globe |
A celestial sphere can also refer to a physical model of the celestial sphere or celestial globe. Such globes map the constellations on the outside of a sphere, resulting in a mirror image of the constellations as seen from Earth. The oldest surviving example of such an artifact is the globe of the Farnese Atlas sculpture, a 2nd-century copy of an older (Hellenistic period, ca. 120 BCE) work.
|
See also: International Celestial Reference System |
Observers on other worlds would, of course, see objects in that sky under much the same conditions – as if projected onto a dome. Coordinate systems based on the sky of that world could be constructed. These could be based on the equivalent "ecliptic", poles and equator, although the reasons for building a system that way are as much historic as technical.