System for representing and reasoning about time
In logic, temporal logic is any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time (for example, "I am always hungry", "I will eventually be hungry", or "I will be hungry until I eat something"). It is sometimes also used to refer to tense logic, a modal logic-based system of temporal logic introduced by Arthur Prior in the late 1950s, with important contributions by Hans Kamp. It has been further developed by computer scientists, notably Amir Pnueli, and logicians.
Temporal logic has found an important application in formal verification, where it is used to state requirements of hardware or software systems. For instance, one may wish to say that whenever a request is made, access to a resource is eventually granted, but it is never granted to two requestors simultaneously. Such a statement can conveniently be expressed in a temporal logic.
Motivation
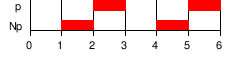
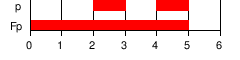
Consider the statement "I am hungry". Though its meaning is constant in time, the statement's truth value can vary in time. Sometimes it is true, and sometimes false, but never simultaneously true and false. In a temporal logic, a statement can have a truth value that varies in time—in contrast with an atemporal logic, which applies only to statements whose truth values are constant in time. This treatment of truth-value over time differentiates temporal logic from computational verb logic.
Temporal logic always has the ability to reason about a timeline. So-called "linear-time" logics are restricted to this type of reasoning. Branching-time logics, however, can reason about multiple timelines. This permits in particular treatment of environments that may act unpredictably.
To continue the example, in a branching-time logic we may state that "there is a possibility that I will stay hungry forever", and that "there is a possibility that eventually I am no longer hungry". If we do not know whether or not I will ever be fed, these statements can both be true.
History
Although Aristotle's logic is almost entirely concerned with the theory of the categorical syllogism, there are passages in his work that are now seen as anticipations of temporal logic, and may imply an early, partially developed form of first-order temporal modal bivalent logic. Aristotle was particularly concerned with the problem of future contingents, where he could not accept that the principle of bivalence applies to statements about future events, i.e. that we can presently decide if a statement about a future event is true or false, such as "there will be a sea battle tomorrow".[1]
There was little development for millennia, Charles Sanders Peirce noted in the 19th century:[2]
Time has usually been considered by logicians to be what is called 'extralogical' matter. I have never shared this opinion. But I have thought that logic had not yet reached the state of development at which the introduction of temporal modifications of its forms would not result in great confusion; and I am much of that way of thinking yet.
Surprisingly for Peirce, the first system of temporal logic was constructed, as far as we know, in the first half of 20th century. Although Arthur Prior is widely known as a founder of temporal logic, the first formalization of such logic was provided in 1947 by Polish logician, Jerzy Łoś.[3] In his work Podstawy Analizy Metodologicznej Kanonów Milla (The Foundations of a Methodological Analysis of Mill’s Methods) he presented a formalization of Mill's canons. In Łoś' approach, emphasis was placed on the time factor. Thus, to reach his goal, he had to create a logic that could provide means for formalization of temporal functions. The logic could be seen as a byproduct of Łoś' main aim,[4] albeit it was the first positional logic that, as a framework, was used later for Łoś' inventions in epistemic logic. The logic itself has syntax very different than Prior's tense logic, which uses modal operators. The language of Łoś' logic rather uses a realization operator, specific to positional logic, which binds the expression with the specific context in which its truth-value is considered. In Łoś' work this considered context was only temporal, thus expressions were bound with specific moments or intervals of time.
In the following years, research of temporal logic by Arthur Prior began.[4] He was concerned with the philosophical implications of free will and predestination. According to his wife, he first considered formalizing temporal logic in 1953. Results of his research were first presented at the conference in Wellington in 1954.[4] The system Prior presented, was similar syntactically to Łoś' logic, although not until 1955 did he explicitly refer to Łoś' work, in the last section of Appendix 1 in Prior’s Formal Logic.[4]
Prior gave lectures on the topic at the University of Oxford in 1955–6, and in 1957 published a book, Time and Modality, in which he introduced a propositional modal logic with two temporal connectives (modal operators), F and P, corresponding to "sometime in the future" and "sometime in the past". In this early work, Prior considered time to be linear. In 1958 however, he received a letter from Saul Kripke, who pointed out that this assumption is perhaps unwarranted. In a development that foreshadowed a similar one in computer science, Prior took this under advisement, and developed two theories of branching time, which he called "Ockhamist" and "Peircean".[2][clarification needed] Between 1958 and 1965 Prior also corresponded with Charles Leonard Hamblin, and a number of early developments in the field can be traced to this correspondence, for example Hamblin implications. Prior published his most mature work on the topic, the book Past, Present, and Future in 1967. He died two years later.[5]
Along with tense logic, Prior constructed a few systems of positional logic, which inherited their main ideas from Łoś.[6] Work in positional temporal logics was continued by Nicholas Rescher in the 60s and 70s. In such works as Note on Chronological Logic (1966), On the Logic of Chronological Propositions (1968), Topological Logic (1968), and Temporal Logic (1971) he researched connections between Łoś' and Prior's systems. Moreover, he proved that Prior's tense operators could be defined using a realization operator in specific positional logics.[6] Rescher, in his work, also created more general systems of positional logics. Although the first ones were constructed for purely temporal uses, he proposed the term topological logics for logics that were meant to contain a realization operator but had no specific temporal axioms—like the clock axiom.
The binary temporal operators Since and Until were introduced by Hans Kamp in his 1968 Ph.D. thesis,[7] which also contains an important result relating temporal logic to first-order logic—a result now known as Kamp's theorem.[8][2][9]
Two early contenders in formal verifications were linear temporal logic, a linear-time logic by Amir Pnueli, and computation tree logic (CTL), a branching-time logic by Mordechai Ben-Ari, Zohar Manna and Amir Pnueli. An almost equivalent formalism to CTL was suggested around the same time by E. M. Clarke and E. A. Emerson. The fact that the second logic can be decided more efficiently than the first does not reflect on branching- and linear-time logics in general, as has sometimes been argued. Rather, Emerson and Lei show that any linear-time logic can be extended to a branching-time logic that can be decided with the same complexity.
Łoś's positional logic
Łoś’s logic was published as his 1947 master’s thesis Podstawy Analizy Metodologicznej Kanonów Milla (The Foundations of a Methodological Analysis of Mill’s Methods).[10] His philosophical and formal concepts could be seen as continuations of those of the Lviv–Warsaw School of Logic, as his supervisor was Jerzy Słupecki, disciple of Jan Łukasiewicz. The paper was not translated into English until 1977, although Henryk Hiż presented in 1951 a brief, but informative, review in the Journal of Symbolic Logic. This review contained core concepts of Łoś’s work and was enough to popularize his results among the logical community. The main aim of this work was to present Mill's canons in the framework of formal logic. To achieve this goal the author researched the importance of temporal functions in the structure of Mill's concept. Having that, he provided his axiomatic system of logic that would fit as a framework for Mill's canons along with their temporal aspects.
Syntax
The language of the logic first published in Podstawy Analizy Metodologicznej Kanonów Milla (The Foundations of a Methodological Analysis of Mill’s Methods) consisted of:[3]
- first-order logic operators ‘¬’, ‘∧’, ‘∨’, ‘→’, ‘≡’, ‘∀’ and ‘∃’
- realization operator U
- functional symbol δ
- propositional variables p1,p2,p3,...
- variables denoting time moments t1,t2,t3,...
- variables denoting time intervals n1,n2,n3,...
The set of terms (denoted by S) is constructed as follows:
- variables denoting time moments or intervals are terms
- if
 and
and  is a time interval variable, then
is a time interval variable, then 
The set of formulas (denoted by For) is constructed as follows:[10]
- all first-order logic formulas are valid
- if
 and
and  is a propositional variable, then
is a propositional variable, then 
- if
 , then
, then 
- if
 and
and  , then
, then 
- if
 and
and  and υ is a propositional, moment or interval variable, then
and υ is a propositional, moment or interval variable, then 
Original Axiomatic System









Prior's tense logic (TL)
The sentential tense logic introduced in Time and Modality has four (non-truth-functional) modal operators (in addition to all usual truth-functional operators in first-order propositional logic).[11]
- P: "It was the case that..." (P stands for "past")
- F: "It will be the case that..." (F stands for "future")
- G: "It always will be the case that..."
- H: "It always was the case that..."
These can be combined if we let π be an infinite path:[12]
 : "At a certain point,
: "At a certain point,  is true at all future states of the path"
is true at all future states of the path" : "
: " is true at infinitely many states on the path"
is true at infinitely many states on the path"
From P and F one can define G and H, and vice versa:

Syntax and semantics
A minimal syntax for TL is specified with the following BNF grammar:

where a is some atomic formula.[13]
Kripke models are used to evaluate the truth of sentences in TL. A pair (T, <) of a set T and a binary relation < on T (called "precedence") is called a frame. A model is given by triple (T, <, V) of a frame and a function V called a valuation that assigns to each pair (a, u) of an atomic formula and a time value some truth value. The notion "ϕ is true in a model U=(T, <, V) at time u" is abbreviated U⊨ϕ[u]. With this notation,[14]
| Statement
|
... is true just when
|
| U⊨a[u]
|
V(a,u)=true
|
| U⊨¬ϕ[u]
|
not U⊨ϕ[u]
|
| U⊨(ϕ∧ψ)[u]
|
U⊨ϕ[u] and U⊨ψ[u]
|
| U⊨(ϕ∨ψ)[u]
|
U⊨ϕ[u] or U⊨ψ[u]
|
| U⊨(ϕ→ψ)[u]
|
U⊨ψ[u] if U⊨ϕ[u]
|
| U⊨Gϕ[u]
|
U⊨ϕ[v] for all v with u<v
|
| U⊨Hϕ[u]
|
U⊨ϕ[v] for all v with v<u
|
Given a class F of frames, a sentence ϕ of TL is
- valid with respect to F if for every model U=(T,<,V) with (T,<) in F and for every u in T, U⊨ϕ[u]
- satisfiable with respect to F if there is a model U=(T,<,V) with (T,<) in F such that for some u in T, U⊨ϕ[u]
- a consequence of a sentence ψ with respect to F if for every model U=(T,<,V) with (T,<) in F and for every u in T, if U⊨ψ[u], then U⊨ϕ[u]
Many sentences are only valid for a limited class of frames. It is common to restrict the class of frames to those with a relation < that is transitive, antisymmetric, reflexive, trichotomic, irreflexive, total, dense, or some combination of these.
A minimal axiomatic logic
Burgess outlines a logic that makes no assumptions on the relation <, but allows for meaningful deductions, based on the following axiom schema:[15]
- A where A is a tautology of first-order logic
- G(A→B)→(GA→GB)
- H(A→B)→(HA→HB)
- A→GPA
- A→HFA
with the following rules of deduction:
- given A→B and A, deduce B (modus ponens)
- given a tautology A, infer GA
- given a tautology A, infer HA
One can derive the following rules:
- Becker's rule: given A→B, deduce TA→TB where T is a tense, any sequence made of G, H, F, and P.
- Mirroring: given a theorem A, deduce its mirror statement A§, which is obtained by replacing G by H (and so F by P) and vice versa.
- Duality: given a theorem A, deduce its dual statement A*, which is obtained by interchanging ∧ with ∨, G with F, and H with P.
Translation to predicate logic
Burgess gives a Meredith translation from statements in TL into statements in first-order logic with one free variable x0 (representing the present moment). This translation M is defined recursively as follows:[16]

where  is the sentence
is the sentence  with all variable indices incremented by 1 and
with all variable indices incremented by 1 and  is a one-place predicate defined by
is a one-place predicate defined by  .
.
Temporal operators
Temporal logic has two kinds of operators: logical operators and modal operators.[17] Logical operators are usual truth-functional operators ( ). The modal operators used in linear temporal logic and computation tree logic are defined as follows.
). The modal operators used in linear temporal logic and computation tree logic are defined as follows.
| Textual
|
Symbolic
|
Definition
|
Explanation
|
Diagram
|
| Binary operators
|
| φ U ψ
|

|

|
Until: ψ holds at the current or a future position, and φ has to hold until that position. At that position φ does not have to hold any more.
|
|
| φ R ψ
|

|

|
Release: φ releases ψ if ψ is true up until and including the first position in which φ is true (or forever if such a position does not exist).
|
|
| Unary operators
|
| N φ
|

|

|
Next: φ has to hold at the next state. (X is used synonymously.)
|
|
| F φ
|

|

|
Future: φ eventually has to hold (somewhere on the subsequent path).
|
|
| G φ
|

|

|
Globally: φ has to hold on the entire subsequent path.
|
|
| A φ
|

|

|
All: φ has to hold on all paths starting from the current state.
|
|
| E φ
|

|

|
Exists: there exists at least one path starting from the current state where φ holds.
|
|
Alternate symbols:
- operator R is sometimes denoted by V
- The operator W is the weak until operator:
 is equivalent to
is equivalent to 
Unary operators are well-formed formulas whenever B(φ) is well-formed. Binary operators are well-formed formulas whenever B(φ) and C(φ) are well-formed.
In some logics, some operators cannot be expressed. For example, N operator cannot be expressed in temporal logic of actions.