
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation for an arbitrary complex number , which represents the order of the Bessel function. Although and produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of .
The most important cases are when is an integer or half-integer. Bessel functions for integer are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer are obtained when solving the Helmholtz equation in spherical coordinates.
Applications of Bessel functions
[edit]Bessel's equation arises when finding separable solutions to Laplace's equation and the Helmholtz equation in cylindrical or spherical coordinates. Bessel functions are therefore especially important for many problems of wave propagation and static potentials. In solving problems in cylindrical coordinate systems, one obtains Bessel functions of integer order (α = n); in spherical problems, one obtains half-integer orders (α = n + 1/2). For example:
- Electromagnetic waves in a cylindrical waveguide
- Pressure amplitudes of inviscid rotational flows
- Heat conduction in a cylindrical object
- Modes of vibration of a thin circular or annular acoustic membrane (such as a drumhead or other membranophone) or thicker plates such as sheet metal (see Kirchhoff–Love plate theory, Mindlin–Reissner plate theory)
- Diffusion problems on a lattice
- Solutions to the radial Schrödinger equation (in spherical and cylindrical coordinates) for a free particle
- Position space representation of the Feynman propagator in quantum field theory
- Solving for patterns of acoustical radiation
- Frequency-dependent friction in circular pipelines
- Dynamics of floating bodies
- Angular resolution
- Diffraction from helical objects, including DNA
- Probability density function of product of two normally distributed random variables[1]
- Analyzing of the surface waves generated by microtremors, in geophysics and seismology.
Bessel functions also appear in other problems, such as signal processing (e.g., see FM audio synthesis, Kaiser window, or Bessel filter).
Definitions
[edit]Because this is a linear differential equation, solutions can be scaled to any amplitude. The amplitudes chosen for the functions originate from the early work in which the functions appeared as solutions to definite integrals rather than solutions to differential equations. Because the differential equation is second-order, there must be two linearly independent solutions. Depending upon the circumstances, however, various formulations of these solutions are convenient. Different variations are summarized in the table below and described in the following sections.
| Type | First kind | Second kind |
|---|---|---|
| Bessel functions | Jα | Yα |
| Modified Bessel functions | Iα | Kα |
| Hankel functions | H(1) α = Jα + iYα |
H(2) α = Jα − iYα |
| Spherical Bessel functions | jn | yn |
| Spherical Hankel functions | h(1) n = jn + iyn |
h(2) n = jn − iyn |
Bessel functions of the second kind and the spherical Bessel functions of the second kind are sometimes denoted by Nn and nn, respectively, rather than Yn and yn.[2][3]
Bessel functions of the first kind: Jα
[edit]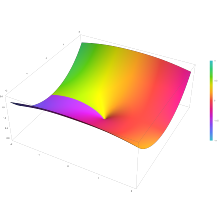

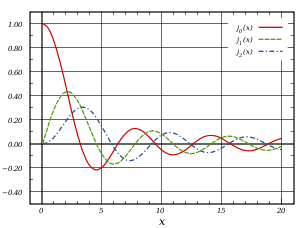
Bessel functions of the first kind, denoted as Jα(x), are solutions of Bessel's differential equation. For integer or positive α, Bessel functions of the first kind are finite at the origin (x = 0); while for negative non-integer α, Bessel functions of the first kind diverge as x approaches zero. It is possible to define the function by times a Maclaurin series (note that α need not be an integer, and non-integer powers are not permitted in a Taylor series), which can be found by applying the Frobenius method to Bessel's equation:[4] where Γ(z) is the gamma function, a shifted generalization of the factorial function to non-integer values. The Bessel function of the first kind is an entire function if α is an integer, otherwise it is a multivalued function with singularity at zero. The graphs of Bessel functions look roughly like oscillating sine or cosine functions that decay proportionally to (see also their asymptotic forms below), although their roots are not generally periodic, except asymptotically for large x. (The series indicates that −J1(x) is the derivative of J0(x), much like −sin x is the derivative of cos x; more generally, the derivative of Jn(x) can be expressed in terms of Jn ± 1(x) by the identities below.)
For non-integer α, the functions Jα(x) and J−α(x) are linearly independent, and are therefore the two solutions of the differential equation. On the other hand, for integer order n, the following relationship is valid (the gamma function has simple poles at each of the non-positive integers):[5]
This means that the two solutions are no longer linearly independent. In this case, the second linearly independent solution is then found to be the Bessel function of the second kind, as discussed below.
Bessel's integrals
[edit]Another definition of the Bessel function, for integer values of n, is possible using an integral representation:[6] which is also called Hansen-Bessel formula.[7]
This was the approach that Bessel used,[8] and from this definition he derived several properties of the function. The definition may be extended to non-integer orders by one of Schläfli's integrals, for Re(x) > 0:[6][9][10][11][12]
Relation to hypergeometric series
[edit]The Bessel functions can be expressed in terms of the generalized hypergeometric series as[13]
This expression is related to the development of Bessel functions in terms of the Bessel–Clifford function.
Relation to Laguerre polynomials
[edit]In terms of the Laguerre polynomials Lk and arbitrarily chosen parameter t, the Bessel function can be expressed as[14]
Bessel functions of the second kind: Yα
[edit]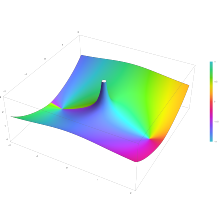
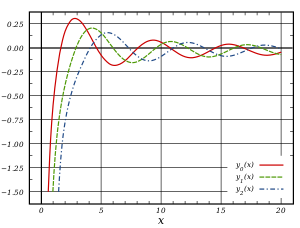
The Bessel functions of the second kind, denoted by Yα(x), occasionally denoted instead by Nα(x), are solutions of the Bessel differential equation that have a singularity at the origin (x = 0) and are multivalued. These are sometimes called Weber functions, as they were introduced by H. M. Weber (1873), and also Neumann functions after Carl Neumann.[15]
For non-integer α, Yα(x) is related to Jα(x) by
In the case of integer order n, the function is defined by taking the limit as a non-integer α tends to n:
If n is a nonnegative integer, we have the series[16]

where is the digamma function, the logarithmic derivative of the gamma function.[17]
There is also a corresponding integral formula (for Re(x) > 0):[18]
In the case where n = 0,
Yα(x) is necessary as the second linearly independent solution of the Bessel's equation when α is an integer. But Yα(x) has more meaning than that. It can be considered as a "natural" partner of Jα(x). See also the subsection on Hankel functions below.
When α is an integer, moreover, as was similarly the case for the functions of the first kind, the following relationship is valid:
Both Jα(x) and Yα(x) are holomorphic functions of x on the complex plane cut along the negative real axis. When α is an integer, the Bessel functions J are entire functions of x. If x is held fixed at a non-zero value, then the Bessel functions are entire functions of α.
The Bessel functions of the second kind when α is an integer is an example of the second kind of solution in Fuchs's theorem.
Hankel functions: H(1)
α, H(2)
α
[edit]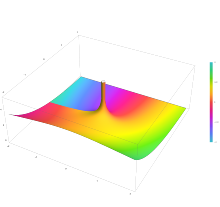
n(x) with n = −0.5 in the complex plane from −2 − 2i to 2 + 2i
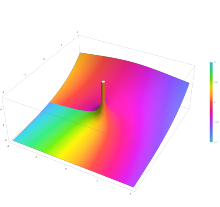
n(x) with n = −0.5 in the complex plane from −2 − 2i to 2 + 2i
Another important formulation of the two linearly independent solutions to Bessel's equation are the Hankel functions of the first and second kind, H(1)
α(x) and H(2)
α(x), defined as[19]
where i is the imaginary unit. These linear combinations are also known as Bessel functions of the third kind; they are two linearly independent solutions of Bessel's differential equation. They are named after Hermann Hankel.
These forms of linear combination satisfy numerous simple-looking properties, like asymptotic formulae or integral representations. Here, "simple" means an appearance of a factor of the form ei f(x). For real where , are real-valued, the Bessel functions of the first and second kind are the real and imaginary parts, respectively, of the first Hankel function and the real and negative imaginary parts of the second Hankel function. Thus, the above formulae are analogs of Euler's formula, substituting H(1)
α(x), H(2)
α(x) for and , for , , as explicitly shown in the asymptotic expansion.
The Hankel functions are used to express outward- and inward-propagating cylindrical-wave solutions of the cylindrical wave equation, respectively (or vice versa, depending on the sign convention for the frequency).
Using the previous relationships, they can be expressed as
If α is an integer, the limit has to be calculated. The following relationships are valid, whether α is an integer or not:[20]
In particular, if α = m + 1/2 with m a nonnegative integer, the above relations imply directly that
These are useful in developing the spherical Bessel functions (see below).
The Hankel functions admit the following integral representations for Re(x) > 0:[21] where the integration limits indicate integration along a contour that can be chosen as follows: from −∞ to 0 along the negative real axis, from 0 to ±πi along the imaginary axis, and from ±πi to +∞ ± πi along a contour parallel to the real axis.[18]
Modified Bessel functions: Iα, Kα
[edit]The Bessel functions are valid even for complex arguments x, and an important special case is that of a purely imaginary argument. In this case, the solutions to the Bessel equation are called the modified Bessel functions (or occasionally the hyperbolic Bessel functions) of the first and second kind and are defined as[22] when α is not an integer; when α is an integer, then the limit is used. These are chosen to be real-valued for real and positive arguments x. The series expansion for Iα(x) is thus similar to that for Jα(x), but without the alternating (−1)m factor.
can be expressed in terms of Hankel functions:
Using these two formulae the result to +, commonly known as Nicholson's integral or Nicholson's formula, can be obtained to give the following
given that the condition Re(x) > 0 is met. It can also be shown that
only when |Re(α)| < 1/2 and Re(x) ≥ 0 but not when x = 0.[23]
We can express the first and second Bessel functions in terms of the modified Bessel functions (these are valid if −π < arg z ≤ π/2):[24]
Iα(x) and Kα(x) are the two linearly independent solutions to the modified Bessel's equation:[25]
Unlike the ordinary Bessel functions, which are oscillating as functions of a real argument, Iα and Kα are exponentially growing and decaying functions respectively. Like the ordinary Bessel function Jα, the function Iα goes to zero at x = 0 for α > 0 and is finite at x = 0 for α = 0. Analogously, Kα diverges at x = 0 with the singularity being of logarithmic type for K0, and 1/2Γ(|α|)(2/x)|α| otherwise.[26]
 |
 |
Two integral formulas for the modified Bessel functions are (for Re(x) > 0):[27]
Bessel functions can be described as Fourier transforms of powers of quadratic functions. For example (for Re(ω) > 0):
It can be proven by showing equality to the above integral definition for K0. This is done by integrating a closed curve in the first quadrant of the complex plane.
Modified Bessel functions K1/3 and K2/3 can be represented in terms of rapidly convergent integrals[28]
The modified Bessel function is useful to represent the Laplace distribution as an Exponential-scale mixture of normal distributions.
The modified Bessel function of the second kind has also been called by the following names (now rare):
- Basset function after Alfred Barnard Basset
- Modified Bessel function of the third kind
- Modified Hankel function[29]
- Macdonald function after Hector Munro Macdonald
Spherical Bessel functions: jn, yn
[edit]
When solving the Helmholtz equation in spherical coordinates by separation of variables, the radial equation has the form
The two linearly independent solutions to this equation are called the spherical Bessel functions jn and yn, and are related to the ordinary Bessel functions Jn and Yn by[30]
yn is also denoted nn or ηn; some authors call these functions the spherical Neumann functions.
From the relations to the ordinary Bessel functions it is directly seen that:
The spherical Bessel functions can also be written as (Rayleigh's formulas)[31]
The zeroth spherical Bessel function j0(x) is also known as the (unnormalized) sinc function. The first few spherical Bessel functions are:[32] and[33]
Generating function
[edit]The spherical Bessel functions have the generating functions[34]
Finite series expansions
[edit]In contrast to the whole integer Bessel functions Jn(x), Yn(x), the spherical Bessel functions jn(x), yn(x) have a finite series expression:[35]
Differential relations
[edit]In the following, fn is any of jn, yn, h(1)
n, h(2)
n for n = 0, ±1, ±2, ...[36]
Spherical Hankel functions: h(1)
n, h(2)
n
[edit]
n(x) with n = -0.5 in the complex plane from −2 − 2i to 2 + 2i

n(x) with n = −0.5 in the complex plane from −2 − 2i to 2 + 2i
There are also spherical analogues of the Hankel functions:
In fact, there are simple closed-form expressions for the Bessel functions of half-integer order in terms of the standard trigonometric functions, and therefore for the spherical Bessel functions. In particular, for non-negative integers n:
and h(2)
n is the complex-conjugate of this (for real x). It follows, for example, that j0(x) = sin x/x and y0(x) = −cos x/x, and so on.
The spherical Hankel functions appear in problems involving spherical wave propagation, for example in the multipole expansion of the electromagnetic field.
Riccati–Bessel functions: Sn, Cn, ξn, ζn
[edit]Riccati–Bessel functions only slightly differ from spherical Bessel functions:
They satisfy the differential equation
For example, this kind of differential equation appears in quantum mechanics while solving the radial component of the Schrödinger's equation with hypothetical cylindrical infinite potential barrier.[37] This differential equation, and the Riccati–Bessel solutions, also arises in the problem of scattering of electromagnetic waves by a sphere, known as Mie scattering after the first published solution by Mie (1908). See e.g., Du (2004)[38] for recent developments and references.
Following Debye (1909), the notation ψn, χn is sometimes used instead of Sn, Cn.
Asymptotic forms
[edit]The Bessel functions have the following asymptotic forms. For small arguments , one obtains, when is not a negative integer:[4]
When α is a negative integer, we have
For the Bessel function of the second kind we have three cases: where γ is the Euler–Mascheroni constant (0.5772...).
For large real arguments z ≫ |α2 − 1/4|, one cannot write a true asymptotic form for Bessel functions of the first and second kind (unless α is half-integer) because they have zeros all the way out to infinity, which would have to be matched exactly by any asymptotic expansion. However, for a given value of arg z one can write an equation containing a term of order |z|−1:[39]
(For α = 1/2 the last terms in these formulas drop out completely; see the spherical Bessel functions above.)
The asymptotic forms for the Hankel functions are:
These can be extended to other values of arg z using equations relating H(1)
α(zeimπ) and H(2)
α(zeimπ) to H(1)
α(z) and H(2)
α(z).[40]
It is interesting that although the Bessel function of the first kind is the average of the two Hankel functions, Jα(z) is not asymptotic to the average of these two asymptotic forms when z is negative (because one or the other will not be correct there, depending on the arg z used). But the asymptotic forms for the Hankel functions permit us to write asymptotic forms for the Bessel functions of first and second kinds for complex (non-real) z so long as |z| goes to infinity at a constant phase angle arg z (using the square root having positive real part):
For the modified Bessel functions, Hankel developed asymptotic (large argument) expansions as well:[41][42]
There is also the asymptotic form (for large real )[43]
When α = 1/2, all the terms except the first vanish, and we have
For small arguments , we have
Properties
[edit]For integer order α = n, Jn is often defined via a Laurent series for a generating function: an approach used by P. A. Hansen in 1843. (This can be generalized to non-integer order by contour integration or other methods.)
Infinite series of Bessel functions in the form where arise in many physical systems and defined in closed form by the Sung series.[44] For example, when N = 3: . More generally, the Sung series and the alternating Sung series are written as:
A series expansion using Bessel functions (Kapteyn series) is
Another important relation for integer orders is the Jacobi–Anger expansion: and which is used to expand a plane wave as a sum of cylindrical waves, or to find the Fourier series of a tone-modulated FM signal.
More generally, a series is called Neumann expansion of f. The coefficients for ν = 0 have the explicit form where Ok is Neumann's polynomial.[45]
Selected functions admit the special representation with due to the orthogonality relation
More generally, if f has a branch-point near the origin of such a nature that then or where is the Laplace transform of f.[46]
Another way to define the Bessel functions is the Poisson representation formula and the Mehler-Sonine formula: where ν > −1/2 and z ∈ C.[47] This formula is useful especially when working with Fourier transforms.
Because Bessel's equation becomes Hermitian (self-adjoint) if it is divided by x, the solutions must satisfy an orthogonality relationship for appropriate boundary conditions. In particular, it follows that: where α > −1, δm,n is the Kronecker delta, and uα,m is the mth zero of Jα(x). This orthogonality relation can then be used to extract the coefficients in the Fourier–Bessel series, where a function is expanded in the basis of the functions Jα(x uα,m) for fixed α and varying m.
An analogous relationship for the spherical Bessel functions follows immediately:
If one defines a boxcar function of x that depends on a small parameter ε as: (where rect is the rectangle function) then the Hankel transform of it (of any given order α > −1/2), gε(k), approaches Jα(k) as ε approaches zero, for any given k. Conversely, the Hankel transform (of the same order) of gε(k) is fε(x): which is zero everywhere except near 1. As ε approaches zero, the right-hand side approaches δ(x − 1), where δ is the Dirac delta function. This admits the limit (in the distributional sense):
A change of variables then yields the closure equation:[48] for α > −1/2. The Hankel transform can express a fairly arbitrary function [clarification needed]as an integral of Bessel functions of different scales. For the spherical Bessel functions the orthogonality relation is: for α > −1.
Another important property of Bessel's equations, which follows from Abel's identity, involves the Wronskian of the solutions: where Aα and Bα are any two solutions of Bessel's equation, and Cα is a constant independent of x (which depends on α and on the particular Bessel functions considered). In particular, and for α > −1.
For α > −1, the even entire function of genus 1, x−αJα(x), has only real zeros. Let be all its positive zeros, then
(There are a large number of other known integrals and identities that are not reproduced here, but which can be found in the references.)
Recurrence relations
[edit]The functions Jα, Yα, H(1)
α, and H(2)
α all satisfy the recurrence relations[49]
and
where Z denotes J, Y, H(1), or H(2). These two identities are often combined, e.g. added or subtracted, to yield various other relations. In this way, for example, one can compute Bessel functions of higher orders (or higher derivatives) given the values at lower orders (or lower derivatives). In particular, it follows that[50]
Modified Bessel functions follow similar relations: and and
The recurrence relation reads where Cα denotes Iα or eαiπKα. These recurrence relations are useful for discrete diffusion problems.
Transcendence
[edit]In 1929, Carl Ludwig Siegel proved that Jν(x), J'ν(x), and the logarithmic derivative J'ν(x)/Jν(x) are transcendental numbers when ν is rational and x is algebraic and nonzero.[51] The same proof also implies that Kν(x) is transcendental under the same assumptions.[52]
Multiplication theorem
[edit]The Bessel functions obey a multiplication theorem where λ and ν may be taken as arbitrary complex numbers.[53][54] For |λ2 − 1| < 1,[53] the above expression also holds if J is replaced by Y. The analogous identities for modified Bessel functions and |λ2 − 1| < 1 are and
Zeros of the Bessel function
[edit]Bourget's hypothesis
[edit]Bessel himself originally proved that for nonnegative integers n, the equation Jn(x) = 0 has an infinite number of solutions in x.[55] When the functions Jn(x) are plotted on the same graph, though, none of the zeros seem to coincide for different values of n except for the zero at x = 0. This phenomenon is known as Bourget's hypothesis after the 19th-century French mathematician who studied Bessel functions. Specifically it states that for any integers n ≥ 0 and m ≥ 1, the functions Jn(x) and Jn + m(x) have no common zeros other than the one at x = 0. The hypothesis was proved by Carl Ludwig Siegel in 1929.[56]
Transcendence
[edit]Siegel proved in 1929 that when ν is rational, all nonzero roots of Jν(x) and J'ν(x) are transcendental,[57] as are all the roots of Kν(x).[52] It is also known that all roots of the higher derivatives for n ≤ 18 are transcendental, except for the special values and .[57]
Numerical approaches
[edit]For numerical studies about the zeros of the Bessel function, see Gil, Segura & Temme (2007), Kravanja et al. (1998) and Moler (2004).
Numerical values
[edit]The first zero in J0 (i.e, j0,1, j0,2 and j0,3) occurs at arguments of approximately 2.40483, 5.52008 and 8.65373, respectively.[58]
See also
[edit]- Anger function
- Bessel polynomials
- Bessel–Clifford function
- Bessel–Maitland function
- Fourier–Bessel series
- Hahn–Exton q-Bessel function
- Hankel transform
- Incomplete Bessel functions
- Jackson q-Bessel function
- Kelvin functions
- Kontorovich–Lebedev transform
- Lentz's algorithm
- Lerche–Newberger sum rule
- Lommel function
- Lommel polynomial
- Neumann polynomial
- Riccati-Bessel Functions
- Schlömilch's series
- Sonine formula
- Struve function
- Vibrations of a circular membrane
- Weber function (defined at Anger function)
- Gauss' circle problem
Notes
[edit]- ^ Wilensky, Michael; Brown, Jordan; Hazelton, Bryna (June 2023). "Why and when to expect Gaussian error distributions in epoch of reionization 21-cm power spectrum measurements". Monthly Notices of the Royal Astronomical Society. 521 (4): 5191–5206. arXiv:2211.13576. doi:10.1093/mnras/stad863.
- ^ Weisstein, Eric W. "Spherical Bessel Function of the Second Kind". MathWorld.
- ^ Weisstein, Eric W. "Bessel Function of the Second Kind". MathWorld.
- ^ a b Abramowitz and Stegun, p. 360, 9.1.10.
- ^ Abramowitz and Stegun, p. 358, 9.1.5.
- ^ a b Temme, Nico M. (1996). Special Functions: An introduction to the classical functions of mathematical physics (2nd print ed.). New York: Wiley. pp. 228–231. ISBN 0471113131.
- ^ Weisstein, Eric W. "Hansen-Bessel Formula". MathWorld.
- ^ Bessel, F. (1824). The relevant integral is an unnumbered equation between equations 28 and 29. Note that Bessel's would today be written .
- ^ Watson, p. 176
- ^ "Properties of Hankel and Bessel Functions". Archived from the original on 2010-09-23. Retrieved 2010-10-18.
- ^ "Integral representations of the Bessel function". www.nbi.dk. Archived from the original on 3 October 2022. Retrieved 25 March 2018.
- ^ Arfken & Weber, exercise 11.1.17.
- ^ Abramowitz and Stegun, p. 362, 9.1.69.
- ^ Szegő, Gábor (1975). Orthogonal Polynomials (4th ed.). Providence, RI: AMS.
- ^ "Bessel Functions of the First and Second Kind" (PDF). mhtlab.uwaterloo.ca. p. 3. Archived (PDF) from the original on 2022-10-09. Retrieved 24 May 2022.
- ^ NIST Digital Library of Mathematical Functions, (10.8.1). Accessed on line Oct. 25, 2016.
- ^ Weisstein, Eric W. "Bessel Function of the Second Kind". MathWorld.
- ^ a b Watson, p. 178.
- ^ Abramowitz and Stegun, p. 358, 9.1.3, 9.1.4.
- ^ Abramowitz and Stegun, p. 358, 9.1.6.
- ^ Abramowitz and Stegun, p. 360, 9.1.25.
- ^ Abramowitz and Stegun, p. 375, 9.6.2, 9.6.10, 9.6.11.
- ^ Dixon; Ferrar, W.L. (1930). "A direct proof of Nicholson's integral". The Quarterly Journal of Mathematics. Oxford: 236–238. doi:10.1093/qmath/os-1.1.236.
- ^ Abramowitz and Stegun, p. 375, 9.6.3, 9.6.5.
- ^ Abramowitz and Stegun, p. 374, 9.6.1.
- ^ Greiner, Walter; Reinhardt, Joachim (2009). Quantum Electrodynamics. Springer. p. 72. ISBN 978-3-540-87561-1.
- ^ Watson, p. 181.
- ^ Khokonov, M. Kh. (2004). "Cascade Processes of Energy Loss by Emission of Hard Photons". Journal of Experimental and Theoretical Physics. 99 (4): 690–707. Bibcode:2004JETP...99..690K. doi:10.1134/1.1826160. S2CID 122599440.. Derived from formulas sourced to I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products (Fizmatgiz, Moscow, 1963; Academic Press, New York, 1980).
- ^ Referred to as such in: Teichroew, D. (1957). "The Mixture of Normal Distributions with Different Variances" (PDF). The Annals of Mathematical Statistics. 28 (2): 510–512. doi:10.1214/aoms/1177706981.
- ^ Abramowitz and Stegun, p. 437, 10.1.1.
- ^ Abramowitz and Stegun, p. 439, 10.1.25, 10.1.26.
- ^ Abramowitz and Stegun, p. 438, 10.1.11.
- ^ Abramowitz and Stegun, p. 438, 10.1.12.
- ^ Abramowitz and Stegun, p. 439, 10.1.39.
- ^ L.V. Babushkina, M.K. Kerimov, A.I. Nikitin, Algorithms for computing Bessel functions of half-integer order with complex arguments, p. 110, p. 111.
- ^ Abramowitz and Stegun, p. 439, 10.1.23, 10.1.24.
- ^ Griffiths. Introduction to Quantum Mechanics, 2nd edition, p. 154.
- ^ Du, Hong (2004). "Mie-scattering calculation". Applied Optics. 43 (9): 1951–1956. Bibcode:2004ApOpt..43.1951D. doi:10.1364/ao.43.001951. PMID 15065726.
- ^ Abramowitz and Stegun, p. 364, 9.2.1.
- ^ NIST Digital Library of Mathematical Functions, Section 10.11.
- ^ Abramowitz and Stegun, p. 377, 9.7.1.
- ^ Abramowitz and Stegun, p. 378, 9.7.2.
- ^ Fröhlich and Spencer 1981 Appendix B
- ^ Sung, S.; Hovden, R. (2022). "On Infinite Series of Bessel functions of the First Kind". arXiv:2211.01148 [math-ph].
- ^ Abramowitz and Stegun, p. 363, 9.1.82 ff.
- ^ Watson, G. N. (25 August 1995). A Treatise on the Theory of Bessel Functions. Cambridge University Press. ISBN 9780521483919. Retrieved 25 March 2018 – via Google Books.
- ^ Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015) [October 2014]. "8.411.10.". In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Table of Integrals, Series, and Products. Translated by Scripta Technica, Inc. (8 ed.). Academic Press, Inc. ISBN 978-0-12-384933-5. LCCN 2014010276.
- ^ Arfken & Weber, section 11.2
- ^ Abramowitz and Stegun, p. 361, 9.1.27.
- ^ Abramowitz and Stegun, p. 361, 9.1.30.
- ^ Siegel, Carl L. (2014). "Über einige Anwendungen diophantischer Approximationen". On Some Applications of Diophantine Approximations: a translation of Carl Ludwig Siegel's Über einige Anwendungen diophantischer Approximationen by Clemens Fuchs, with a commentary and the article Integral points on curves: Siegel's theorem after Siegel's proof by Clemens Fuchs and Umberto Zannier (in German). Scuola Normale Superiore. pp. 81–138. doi:10.1007/978-88-7642-520-2_2. ISBN 978-88-7642-520-2.
- ^ a b James, R. D. (November 1950). "Review: Carl Ludwig Siegel, Transcendental numbers". Bulletin of the American Mathematical Society. 56 (6): 523–526. doi:10.1090/S0002-9904-1950-09435-X.
- ^ a b Abramowitz and Stegun, p. 363, 9.1.74.
- ^ Truesdell, C. (1950). "On the Addition and Multiplication Theorems for the Special Functions". Proceedings of the National Academy of Sciences. 1950 (12): 752–757. Bibcode:1950PNAS...36..752T. doi:10.1073/pnas.36.12.752. PMC 1063284. PMID 16578355.
- ^ Bessel, F. (1824), article 14.
- ^ Watson, pp. 484–485.
- ^ a b Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions". International Journal of Mathematics and Mathematical Sciences. 18 (3): 551–560. doi:10.1155/S0161171295000706.
- ^ Abramowitz & Stegun, p409
References
[edit]- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 9". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. pp. 355, 435. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253. See also chapter 10.
- Arfken, George B. and Hans J. Weber, Mathematical Methods for Physicists, 6th edition (Harcourt: San Diego, 2005). ISBN 0-12-059876-0.
- Bessel, Friedrich (1824). "Untersuchung des Theils der planetarischen Störungen, welcher aus der Bewegung der Sonne entsteht" [Investigation of the part of the planetary disturbances which arise from the movement of the sun]. Berlin Abhandlungen. Reproduced as pages 84 to 109 in Abhandlungen von Friedrich Wilhelm Bessel. Leipzig: Engelmann. 1875. English translation of the text.
- Bowman, Frank Introduction to Bessel Functions (Dover: New York, 1958). ISBN 0-486-60462-4.
- Gil, A.; Segura, J.; Temme, N. M. (2007). Numerical methods for special functions. Society for Industrial and Applied Mathematics.
- Kravanja, P.; Ragos, O.; Vrahatis, M.N.; Zafiropoulos, F.A. (1998), "ZEBEC: A mathematical software package for computing simple zeros of Bessel functions of real order and complex argument", Computer Physics Communications, 113 (2–3): 220–238, Bibcode:1998CoPhC.113..220K, doi:10.1016/S0010-4655(98)00064-2
- Mie, G. (1908). "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen". Annalen der Physik. 25 (3): 377. Bibcode:1908AnP...330..377M. doi:10.1002/andp.19083300302.
- Olver, F. W. J.; Maximon, L. C. (2010), "Bessel function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248..
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007), "Section 6.5. Bessel Functions of Integer Order", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, archived from the original on 2021-02-03, retrieved 2022-09-28.
- B Spain, M. G. Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 9 deals with Bessel functions.
- N. M. Temme, Special Functions. An Introduction to the Classical Functions of Mathematical Physics, John Wiley and Sons, Inc., New York, 1996. ISBN 0-471-11313-1. Chapter 9 deals with Bessel functions.
- Watson, G. N., A Treatise on the Theory of Bessel Functions, Second Edition, (1995) Cambridge University Press. ISBN 0-521-48391-3.
- Weber, Heinrich (1873), "Ueber eine Darstellung willkürlicher Functionen durch Bessel'sche Functionen", Mathematische Annalen, 6 (2): 146–161, doi:10.1007/BF01443190, S2CID 122409461.
External links
[edit]- Lizorkin, P. I. (2001) [1994], "Bessel functions", Encyclopedia of Mathematics, EMS Press.
- Karmazina, L. N.; Prudnikov, A.P. (2001) [1994], "Cylinder function", Encyclopedia of Mathematics, EMS Press.
- Rozov, N. Kh. (2001) [1994], "Bessel equation", Encyclopedia of Mathematics, EMS Press.
- Wolfram function pages on Bessel J and Y functions, and modified Bessel I and K functions. Pages include formulas, function evaluators, and plotting calculators.
- Weisstein, Eric W. "Bessel functions of the first kind". MathWorld.
- Bessel functions Jν, Yν, Iν and Kν in Librow Function handbook.
- F. W. J. Olver, L. C. Maximon, Bessel Functions (chapter 10 of the Digital Library of Mathematical Functions).
- Moler, C. B. (2004). Numerical Computing with MATLAB (PDF). Society for Industrial and Applied Mathematics. Archived from the original (PDF) on 2017-08-08.


















![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&=J_{\alpha }(x)+iY_{\alpha }(x),\\[5pt]H_{\alpha }^{(2)}(x)&=J_{\alpha }(x)-iY_{\alpha }(x),\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa434f6bcee175b4ff90fde5ba2fb596a41b90c3)






![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin \alpha \pi )),\\[5pt]H_{\alpha }^{(2)}(x)&={\frac {J_{-\alpha }(x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin \alpha \pi )).\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2748efe7f4138a71b2bf84ed77bc90d4bf0810)
![{\displaystyle {\begin{aligned}H_{-\alpha }^{(1)}(x)&=e^{\alpha \pi i}H_{\alpha }^{(1)}(x),\\[6mu]H_{-\alpha }^{(2)}(x)&=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x).\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f0226c9673919c5c9a95041395384711081474)
![{\displaystyle {\begin{aligned}J_{-(m+{\frac {1}{2)))}(x)&=(-1)^{m+1}Y_{m+{\frac {1}{2))}(x),\\[5pt]Y_{-(m+{\frac {1}{2)))}(x)&=(-1)^{m}J_{m+{\frac {1}{2))}(x).\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9f3ac2da371d4ddcb7b0694f5e7fca8c7453803)
![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {1}{\pi i))\int _{-\infty }^{+\infty +\pi i}e^{x\sinh t-\alpha t}\,dt,\\[5pt]H_{\alpha }^{(2)}(x)&=-{\frac {1}{\pi i))\int _{-\infty }^{+\infty -\pi i}e^{x\sinh t-\alpha t}\,dt,\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28973dd4cdae45d03d4ed47926313658638682d6)
![{\displaystyle {\begin{aligned}I_{\alpha }(x)&=i^{-\alpha }J_{\alpha }(ix)=\sum _{m=0}^{\infty }{\frac {1}{m!\,\Gamma (m+\alpha +1)))\left({\frac {x}{2))\right)^{2m+\alpha },\\[5pt]K_{\alpha }(x)&={\frac {\pi }{2)){\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin \alpha \pi )),\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a0b68640cfbec56a6b6ad53c432371549dcfedd)






![{\displaystyle {\begin{aligned}J_{\alpha }(iz)&=e^{\frac {\alpha \pi i}{2))I_{\alpha }(z),\\[1ex]Y_{\alpha }(iz)&=e^{\frac {(\alpha +1)\pi i}{2))I_{\alpha }(z)-{\tfrac {2}{\pi ))e^{-{\frac {\alpha \pi i}{2))}K_{\alpha }(z).\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4460424d9d6b98161589dd4aa46ad6429678c189)

![{\displaystyle {\begin{aligned}I_{\alpha }(x)&={\frac {1}{\pi ))\int _{0}^{\pi }e^{x\cos \theta }\cos \alpha \theta \,d\theta -{\frac {\sin \alpha \pi }{\pi ))\int _{0}^{\infty }e^{-x\cosh t-\alpha t}\,dt,\\[5pt]K_{\alpha }(x)&=\int _{0}^{\infty }e^{-x\cosh t}\cosh \alpha t\,dt.\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c907de8d37caf8e5e482ce5005e8941ab401bd4b)

![{\displaystyle {\begin{aligned}K_{\frac {1}{3))(\xi )&={\sqrt {3))\int _{0}^{\infty }\exp \left(-\xi \left(1+{\frac {4x^{2)){3))\right){\sqrt {1+{\frac {x^{2)){3))))\right)\,dx,\\[5pt]K_{\frac {2}{3))(\xi )&={\frac {1}{\sqrt {3))}\int _{0}^{\infty }{\frac {3+2x^{2)){\sqrt {1+{\frac {x^{2)){3))))}\exp \left(-\xi \left(1+{\frac {4x^{2)){3))\right){\sqrt {1+{\frac {x^{2)){3))))\right)\,dx.\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/526dd0ae355e44f4bd2608b20d39d07da0fff979)








![{\displaystyle {\begin{alignedat}{2}j_{n}(x)&={\frac {\pi }{2x))J_{n+{\frac {1}{2))}(x)=\\&={\frac {1}{2x))\left[e^{ix}\sum _{r=0}^{n}{\frac {i^{r-n-1}(n+r)!}{r!(n-r)!(2x)^{r))}+e^{-ix}\sum _{r=0}^{n}{\frac {(-i)^{r-n-1}(n+r)!}{r!(n-r)!(2x)^{r))}\right]\\&={\frac {1}{x))\left[\sin \left(x-{\frac {n\pi }{2))\right)\sum _{r=0}^{\left[{\frac {n}{2))\right]}{\frac {(-1)^{r}(n+2r)!}{(2r)!(n-2r)!(2x)^{2r))}+\cos \left(x-{\frac {n\pi }{2))\right)\sum _{r=0}^{\left[{\frac {n-1}{2))\right]}{\frac {(-1)^{r}(n+2r+1)!}{(2r+1)!(n-2r-1)!(2x)^{2r+1))}\right]\\y_{n}(x)&=(-1)^{n+1}j_{-n-1}(x)=(-1)^{n+1}{\frac {\pi }{2x))J_{-\left(n+{\frac {1}{2))\right)}(x)=\\&={\frac {(-1)^{n+1)){2x))\left[e^{ix}\sum _{r=0}^{n}{\frac {i^{r+n}(n+r)!}{r!(n-r)!(2x)^{r))}+e^{-ix}\sum _{r=0}^{n}{\frac {(-i)^{r+n}(n+r)!}{r!(n-r)!(2x)^{r))}\right]=\\&={\frac {(-1)^{n+1)){x))\left[\cos \left(x-{\frac {n\pi }{2))\right)\sum _{r=0}^{\left[{\frac {n}{2))\right]}{\frac {(-1)^{r}(n+2r)!}{(2r)!(n-2r)!(2x)^{2r))}+\sin \left(x-{\frac {n\pi }{2))\right)\sum _{r=0}^{\left[{\frac {n-1}{2))\right]}{\frac {(-1)^{r}(n+2r+1)!}{(2r+1)!(n-2r-1)!(2x)^{2r+1))}\right]\end{alignedat))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bb3372a5d9d734b5aa2e867e7d28a7a2b825cd2)








![{\displaystyle Y_{\alpha }(z)\sim {\begin{cases}{\dfrac {2}{\pi ))\left(\ln \left({\dfrac {z}{2))\right)+\gamma \right)&{\text{if ))\alpha =0\\[1ex]-{\dfrac {\Gamma (\alpha )}{\pi ))\left({\dfrac {2}{z))\right)^{\alpha }+{\dfrac {1}{\Gamma (\alpha +1)))\left({\dfrac {z}{2))\right)^{\alpha }\cot(\alpha \pi )&{\text{if ))\alpha {\text{ is a positive integer (one term dominates unless ))\alpha {\text{ is imaginary))),\\[1ex]-{\dfrac {(-1)^{\alpha }\Gamma (-\alpha )}{\pi ))\left({\dfrac {z}{2))\right)^{\alpha }&{\text{if ))\alpha {\text{ is a negative integer,))\end{cases))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0478d18ffc1f12108ee81de9db5e1f89f322db6)


![{\displaystyle {\begin{aligned}J_{\alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z))}e^{i\left(z-{\frac {\alpha \pi }{2))-{\frac {\pi }{4))\right)}&&{\text{for ))-\pi <\arg z<0,\\[1ex]J_{\alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z))}e^{-i\left(z-{\frac {\alpha \pi }{2))-{\frac {\pi }{4))\right)}&&{\text{for ))0<\arg z<\pi ,\\[1ex]Y_{\alpha }(z)&\sim -i{\frac {1}{\sqrt {2\pi z))}e^{i\left(z-{\frac {\alpha \pi }{2))-{\frac {\pi }{4))\right)}&&{\text{for ))-\pi <\arg z<0,\\[1ex]Y_{\alpha }(z)&\sim i{\frac {1}{\sqrt {2\pi z))}e^{-i\left(z-{\frac {\alpha \pi }{2))-{\frac {\pi }{4))\right)}&&{\text{for ))0<\arg z<\pi .\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c892df890c00f5a4bc2d13ae3b02ea0abb79aec1)


![{\displaystyle {\begin{aligned}I_{\alpha }(z)={\frac {1}((\sqrt {2\pi z)){\sqrt[{4}]{1+{\frac {\alpha ^{2)){z^{2))))))}\exp \left(-\alpha \operatorname {arsinh} \left({\frac {\alpha }{z))\right)+z{\sqrt {1+{\frac {\alpha ^{2)){z^{2))))}\right)\left(1+{\mathcal {O))\left({\frac {1}{z{\sqrt {1+{\frac {\alpha ^{2)){z^{2))))))}\right)\right).\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f57e4803db262b5efdc20c32da3835c3fd4f0f9d)
![{\displaystyle {\begin{aligned}I_((1}/{2))(z)&={\sqrt {\frac {2}{\pi ))}{\frac {\sinh(z)}{\sqrt {z))}\sim {\frac {e^{z)){\sqrt {2\pi z))}&&{\text{for ))\left|\arg z\right|<{\tfrac {\pi }{2)),\\[1ex]K_((1}/{2))(z)&={\sqrt {\frac {\pi }{2))}{\frac {e^{-z)){\sqrt {z))}.\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec3a7941e679aaacaf61d90117613ee90a23851)

![{\displaystyle {\begin{aligned}I_{\alpha }(z)&\sim {\frac {1}{\Gamma (\alpha +1)))\left({\frac {z}{2))\right)^{\alpha },\\[1ex]K_{\alpha }(z)&\sim {\begin{cases}-\ln \left({\dfrac {z}{2))\right)-\gamma &{\text{if ))\alpha =0\\[1ex]{\frac {\Gamma (\alpha )}{2))\left({\dfrac {2}{z))\right)^{\alpha }&{\text{if ))\alpha >0\end{cases))\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfbbf3eae419f2a44adfb496e7ccb657439bdaf7)



![{\textstyle \sum _{\nu =-\infty }^{\infty }J_{3\nu +p}(x)={\frac {1}{3))\left[1+2\cos {(x{\sqrt {3))/2-2\pi p/3)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eaa4c63e9da373d3678e16136bd9a11688985bd)














![{\displaystyle {\begin{aligned}J_{\nu }(z)&={\frac {\left({\frac {z}{2))\right)^{\nu )){\Gamma \left(\nu +{\frac {1}{2))\right){\sqrt {\pi ))))\int _{-1}^{1}e^{izs}\left(1-s^{2}\right)^{\nu -{\frac {1}{2))}\,ds\\[5px]&={\frac {2}((\left({\frac {z}{2))\right)}^{\nu }\cdot {\sqrt {\pi ))\cdot \Gamma \left({\frac {1}{2))-\nu \right)))\int _{1}^{\infty }{\frac {\sin zu}{\left(u^{2}-1\right)^{\nu +{\frac {1}{2))))}\,du\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
![{\displaystyle \int _{0}^{1}xJ_{\alpha }\left(xu_{\alpha ,m}\right)J_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n)){2))\left[J_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2}={\frac {\delta _{m,n)){2))\left[J_{\alpha }'\left(u_{\alpha ,m}\right)\right]^{2))](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
![{\displaystyle \int _{0}^{1}x^{2}j_{\alpha }\left(xu_{\alpha ,m}\right)j_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n)){2))\left[j_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2))](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)












![{\displaystyle {\begin{aligned}\left({\frac {1}{x)){\frac {d}{dx))\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]&=x^{\alpha -m}Z_{\alpha -m}(x),\\\left({\frac {1}{x)){\frac {d}{dx))\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha ))}\right]&=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m))}.\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)



![{\displaystyle {\begin{aligned}C_{\alpha -1}(x)-C_{\alpha +1}(x)&={\frac {2\alpha }{x))C_{\alpha }(x),\\[1ex]C_{\alpha -1}(x)+C_{\alpha +1}(x)&=2{\frac {d}{dx))C_{\alpha }(x),\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8390e0da90e49d8017a003ce6e00d8a2358dc06)







