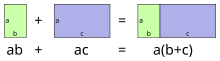
Property involving two mathematical operations
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
 is always true in elementary algebra.
For example, in elementary arithmetic, one has
is always true in elementary algebra.
For example, in elementary arithmetic, one has
 Therefore, one would say that multiplication distributes over addition.
Therefore, one would say that multiplication distributes over addition.
This basic property of numbers is part of the definition of most algebraic structures that have two operations called addition and multiplication, such as complex numbers, polynomials, matrices, rings, and fields. It is also encountered in Boolean algebra and mathematical logic, where each of the logical and (denoted  ) and the logical or (denoted
) and the logical or (denoted  ) distributes over the other.
) distributes over the other.
Definition
Given a set  and two binary operators
and two binary operators  and
and  on
on 
- the operation
 is left-distributive over (or with respect to)
is left-distributive over (or with respect to)  if, given any elements
if, given any elements  of
of 

- the operation
 is right-distributive over
is right-distributive over  if, given any elements
if, given any elements  of
of 

- and the operation
 is distributive over
is distributive over  if it is left- and right-distributive.[1]
if it is left- and right-distributive.[1]
When  is commutative, the three conditions above are logically equivalent.
is commutative, the three conditions above are logically equivalent.
Meaning
The operators used for examples in this section are those of the usual addition  and multiplication
and multiplication 
If the operation denoted  is not commutative, there is a distinction between left-distributivity and right-distributivity:
is not commutative, there is a distinction between left-distributivity and right-distributivity:


In either case, the distributive property can be described in words as:
To multiply a sum (or difference) by a factor, each summand (or minuend and subtrahend) is multiplied by this factor and the resulting products are added (or subtracted).
If the operation outside the parentheses (in this case, the multiplication) is commutative, then left-distributivity implies right-distributivity and vice versa, and one talks simply of distributivity.
One example of an operation that is "only" right-distributive is division, which is not commutative:
 In this case, left-distributivity does not apply:
In this case, left-distributivity does not apply:

The distributive laws are among the axioms for rings (like the ring of integers) and fields (like the field of rational numbers). Here multiplication is distributive over addition, but addition is not distributive over multiplication. Examples of structures with two operations that are each distributive over the other are Boolean algebras such as the algebra of sets or the switching algebra.
Multiplying sums can be put into words as follows: When a sum is multiplied by a sum, multiply each summand of a sum with each summand of the other sum (keeping track of signs) then add up all of the resulting products.
Examples
Real numbers
In the following examples, the use of the distributive law on the set of real numbers  is illustrated. When multiplication is mentioned in elementary mathematics, it usually refers to this kind of multiplication. From the point of view of algebra, the real numbers form a field, which ensures the validity of the distributive law.
is illustrated. When multiplication is mentioned in elementary mathematics, it usually refers to this kind of multiplication. From the point of view of algebra, the real numbers form a field, which ensures the validity of the distributive law.
- First example (mental and written multiplication)
- During mental arithmetic, distributivity is often used unconsciously:
 Thus, to calculate
Thus, to calculate  in one's head, one first multiplies
in one's head, one first multiplies  and
and  and add the intermediate results. Written multiplication is also based on the distributive law.
and add the intermediate results. Written multiplication is also based on the distributive law.
- Second example (with variables)
-

- Third example (with two sums)
-
 Here the distributive law was applied twice, and it does not matter which bracket is first multiplied out.
Here the distributive law was applied twice, and it does not matter which bracket is first multiplied out.
- Fourth example
- Here the distributive law is applied the other way around compared to the previous examples. Consider
 Since the factor
Since the factor  occurs in all summands, it can be factored out. That is, due to the distributive law one obtains
occurs in all summands, it can be factored out. That is, due to the distributive law one obtains

Matrices
The distributive law is valid for matrix multiplication. More precisely,
 for all
for all  -matrices
-matrices  and
and  -matrices
-matrices  as well as
as well as
 for all
for all  -matrices
-matrices  and
and  -matrices
-matrices  Because the commutative property does not hold for matrix multiplication, the second law does not follow from the first law. In this case, they are two different laws.
Because the commutative property does not hold for matrix multiplication, the second law does not follow from the first law. In this case, they are two different laws.
Other examples
- Multiplication of ordinal numbers, in contrast, is only left-distributive, not right-distributive.
- The cross product is left- and right-distributive over vector addition, though not commutative.
- The union of sets is distributive over intersection, and intersection is distributive over union.
- Logical disjunction ("or") is distributive over logical conjunction ("and"), and vice versa.
- For real numbers (and for any totally ordered set), the maximum operation is distributive over the minimum operation, and vice versa:

- For integers, the greatest common divisor is distributive over the least common multiple, and vice versa:

- For real numbers, addition distributes over the maximum operation, and also over the minimum operation:

- For binomial multiplication, distribution is sometimes referred to as the FOIL Method[2] (First terms
 Outer
Outer  Inner
Inner  and Last
and Last  ) such as:
) such as: 
- In all semirings, including the complex numbers, the quaternions, polynomials, and matrices, multiplication distributes over addition:

- In all algebras over a field, including the octonions and other non-associative algebras, multiplication distributes over addition.
Distributivity and rounding
In approximate arithmetic, such as floating-point arithmetic, the distributive property of multiplication (and division) over addition may fail because of the limitations of arithmetic precision. For example, the identity  fails in decimal arithmetic, regardless of the number of significant digits. Methods such as banker's rounding may help in some cases, as may increasing the precision used, but ultimately some calculation errors are inevitable.
fails in decimal arithmetic, regardless of the number of significant digits. Methods such as banker's rounding may help in some cases, as may increasing the precision used, but ultimately some calculation errors are inevitable.
In rings and other structures
Distributivity is most commonly found in semirings, notably the particular cases of rings and distributive lattices.
A semiring has two binary operations, commonly denoted  and
and  and requires that
and requires that  must distribute over
must distribute over 
A ring is a semiring with additive inverses.
A lattice is another kind of algebraic structure with two binary operations,  If either of these operations distributes over the other (say
If either of these operations distributes over the other (say  distributes over
distributes over  ), then the reverse also holds (
), then the reverse also holds ( distributes over
distributes over  ), and the lattice is called distributive. See also Distributivity (order theory).
), and the lattice is called distributive. See also Distributivity (order theory).
A Boolean algebra can be interpreted either as a special kind of ring (a Boolean ring) or a special kind of distributive lattice (a Boolean lattice). Each interpretation is responsible for different distributive laws in the Boolean algebra.
Similar structures without distributive laws are near-rings and near-fields instead of rings and division rings. The operations are usually defined to be distributive on the right but not on the left.
Generalizations
In several mathematical areas, generalized distributivity laws are considered. This may involve the weakening of the above conditions or the extension to infinitary operations. Especially in order theory one finds numerous important variants of distributivity, some of which include infinitary operations, such as the infinite distributive law; others being defined in the presence of only one binary operation, such as the according definitions and their relations are given in the article distributivity (order theory). This also includes the notion of a completely distributive lattice.
In the presence of an ordering relation, one can also weaken the above equalities by replacing  by either
by either  or
or  Naturally, this will lead to meaningful concepts only in some situations. An application of this principle is the notion of sub-distributivity as explained in the article on interval arithmetic.
Naturally, this will lead to meaningful concepts only in some situations. An application of this principle is the notion of sub-distributivity as explained in the article on interval arithmetic.
In category theory, if  and
and  are monads on a category
are monads on a category  a distributive law
a distributive law  is a natural transformation
is a natural transformation  such that
such that  is a lax map of monads
is a lax map of monads  and
and  is a colax map of monads
is a colax map of monads  This is exactly the data needed to define a monad structure on
This is exactly the data needed to define a monad structure on  : the multiplication map is
: the multiplication map is  and the unit map is
and the unit map is  See: distributive law between monads.
See: distributive law between monads.
A generalized distributive law has also been proposed in the area of information theory.
Antidistributivity
The ubiquitous identity that relates inverses to the binary operation in any group, namely  which is taken as an axiom in the more general context of a semigroup with involution, has sometimes been called an antidistributive property (of inversion as a unary operation).[5]
which is taken as an axiom in the more general context of a semigroup with involution, has sometimes been called an antidistributive property (of inversion as a unary operation).[5]
In the context of a near-ring, which removes the commutativity of the additively written group and assumes only one-sided distributivity, one can speak of (two-sided) distributive elements but also of antidistributive elements. The latter reverse the order of (the non-commutative) addition; assuming a left-nearring (i.e. one which all elements distribute when multiplied on the left), then an antidistributive element  reverses the order of addition when multiplied to the right:
reverses the order of addition when multiplied to the right:  [6]
[6]
In the study of propositional logic and Boolean algebra, the term antidistributive law is sometimes used to denote the interchange between conjunction and disjunction when implication factors over them:[7]


These two tautologies are a direct consequence of the duality in De Morgan's laws.