




| Arithmetic operations | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Multiplication (often denoted by the cross symbol ×, by the mid-line dot operator ⋅, by juxtaposition, or, on computers, by an asterisk *) is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a product.
The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the multiplicand, as the quantity of the other one, the multiplier; both numbers can be referred to as factors.
For example, 4 multiplied by 3, often written as and spoken as "3 times 4", can be calculated by adding 3 copies of 4 together:
Here, 3 (the multiplier) and 4 (the multiplicand) are the factors, and 12 is the product.
One of the main properties of multiplication is the commutative property, which states in this case that adding 3 copies of 4 gives the same result as adding 4 copies of 3:
Thus, the designation of multiplier and multiplicand does not affect the result of the multiplication.[1]
Systematic generalizations of this basic definition define the multiplication of integers (including negative numbers), rational numbers (fractions), and real numbers.
Multiplication can also be visualized as counting objects arranged in a rectangle (for whole numbers) or as finding the area of a rectangle whose sides have some given lengths. The area of a rectangle does not depend on which side is measured first—a consequence of the commutative property.
The product of two measurements (or physical quantities) is a new type of measurement, usually with a derived unit. For example, multiplying the lengths (in meters or feet) of the two sides of a rectangle gives its area (in square meters or square feet). Such a product is the subject of dimensional analysis.
The inverse operation of multiplication is division. For example, since 4 multiplied by 3 equals 12, 12 divided by 3 equals 4. Indeed, multiplication by 3, followed by division by 3, yields the original number. The division of a number other than 0 by itself equals 1.
Several mathematical concepts expand upon the fundamental idea of multiplication. The product of a sequence, vector multiplication, complex numbers, and matrices are all examples where this can be seen. These more advanced constructs tend to affect the basic properties in their own ways, such as becoming noncommutative in matrices and some forms of vector multiplication or changing the sign of complex numbers.
Notation
[edit]| × ⋅ | |
|---|---|
Multiplication signs | |
| In Unicode | U+00D7 × MULTIPLICATION SIGN (×) U+22C5 ⋅ DOT OPERATOR (⋅) |
| Different from | |
| Different from | U+00B7 · MIDDLE DOT U+002E . FULL STOP |
In arithmetic, multiplication is often written using the multiplication sign (either × or ) between the terms (that is, in infix notation).[2] For example,
- ("two times three equals six")
There are other mathematical notations for multiplication:
- To reduce confusion between the multiplication sign × and the common variable x, multiplication is also denoted by dot signs,[3] usually a middle-position dot (rarely period): .
- The middle dot notation or dot operator, encoded in Unicode as U+22C5 ⋅ DOT OPERATOR, is now standard in the United States and other countries where the period is used as a decimal point. When the dot operator character is not accessible, the interpunct (·) is used. In other countries that use a comma as a decimal mark, either the period or a middle dot is used for multiplication.[citation needed]
- Historically, in the United Kingdom and Ireland, the middle dot was sometimes used for the decimal to prevent it from disappearing in the ruled line, and the period/full stop was used for multiplication. However, since the Ministry of Technology ruled to use the period as the decimal point in 1968,[4] and the International System of Units (SI) standard has since been widely adopted, this usage is now found only in the more traditional journals such as The Lancet.[5]
- In algebra, multiplication involving variables is often written as a juxtaposition (e.g., for times or for five times ), also called implied multiplication.[6] The notation can also be used for quantities that are surrounded by parentheses (e.g., , or for five times two). This implicit usage of multiplication can cause ambiguity when the concatenated variables happen to match the name of another variable, when a variable name in front of a parenthesis can be confused with a function name, or in the correct determination of the order of operations.[7][8]
- In vector multiplication, there is a distinction between the cross and the dot symbols. The cross symbol generally denotes the taking a cross product of two vectors, yielding a vector as its result, while the dot denotes taking the dot product of two vectors, resulting in a scalar.
In computer programming, the asterisk (as in 5*2) is still the most common notation. This is due to the fact that most computers historically were limited to small character sets (such as ASCII and EBCDIC) that lacked a multiplication sign (such as ⋅ or ×), while the asterisk appeared on every keyboard.[citation needed] This usage originated in the FORTRAN programming language.[9]
The numbers to be multiplied are generally called the "factors" (as in factorization). The number to be multiplied is the "multiplicand", and the number by which it is multiplied is the "multiplier". Usually, the multiplier is placed first, and the multiplicand is placed second;[1] however, sometimes the first factor is the multiplicand and the second the multiplier.[10] Also, as the result of multiplication does not depend on the order of the factors, the distinction between "multiplicand" and "multiplier" is useful only at a very elementary level and in some multiplication algorithms, such as the long multiplication. Therefore, in some sources, the term "multiplicand" is regarded as a synonym for "factor".[11] In algebra, a number that is the multiplier of a variable or expression (e.g., the 3 in ) is called a coefficient.
The result of a multiplication is called a product. When one factor is an integer, the product is a multiple of the other or of the product of the others. Thus, is a multiple of , as is . A product of integers is a multiple of each factor; for example, 15 is the product of 3 and 5 and is both a multiple of 3 and a multiple of 5.
Definitions
[edit]The product of two numbers or the multiplication between two numbers can be defined for common special cases: natural numbers, integers, rational numbers, real numbers, complex numbers, and quaternions.
Product of two natural numbers
[edit]
The product of two natural numbers is defined as:
Product of two integers
[edit]An integer can be either zero, a nonzero natural number, or minus a nonzero natural number. The product of zero and another integer is always zero. The product of two nonzero integers is determined by the product of their positive amounts, combined with the sign derived from the following rule:
(This rule is a consequence of the distributivity of multiplication over addition, and is not an additional rule.)
In words:
- A positive number multiplied by a positive number is positive (product of natural numbers),
- A positive number multiplied by a negative number is negative,
- A negative number multiplied by a positive number is negative,
- A negative number multiplied by a negative number is positive.
Product of two fractions
[edit]Two fractions can be multiplied by multiplying their numerators and denominators:
- which is defined when .
Product of two real numbers
[edit]There are several equivalent ways to define formally the real numbers; see Construction of the real numbers. The definition of multiplication is a part of all these definitions.
A fundamental aspect of these definitions is that every real number can be approximated to any accuracy by rational numbers. A standard way for expressing this is that every real number is the least upper bound of a set of rational numbers. In particular, every positive real number is the least upper bound of the truncations of its infinite decimal representation; for example, is the least upper bound of
A fundamental property of real numbers is that rational approximations are compatible with arithmetic operations, and, in particular, with multiplication. This means that, if a and b are positive real numbers such that and then In particular, the product of two positive real numbers is the least upper bound of the term-by-term products of the sequences of their decimal representations.
As changing the signs transforms least upper bounds into greatest lower bounds, the simplest way to deal with a multiplication involving one or two negative numbers, is to use the rule of signs described above in § Product of two integers. The construction of the real numbers through Cauchy sequences is often preferred in order to avoid consideration of the four possible sign configurations.
Product of two complex numbers
[edit]Two complex numbers can be multiplied by the distributive law and the fact that , as follows:

Geometric meaning of complex multiplication can be understood rewriting complex numbers in polar coordinates:
Furthermore,
from which one obtains
The geometric meaning is that the magnitudes are multiplied and the arguments are added.
Product of two quaternions
[edit]The product of two quaternions can be found in the article on quaternions. Note, in this case, that and are in general different.
Computation
[edit]
Many common methods for multiplying numbers using pencil and paper require a multiplication table of memorized or consulted products of small numbers (typically any two numbers from 0 to 9). However, one method, the peasant multiplication algorithm, does not. The example below illustrates "long multiplication" (the "standard algorithm", "grade-school multiplication"):
23958233
× 5830
———————————————
00000000 ( = 23,958,233 × 0)
71874699 ( = 23,958,233 × 30)
191665864 ( = 23,958,233 × 800)
+ 119791165 ( = 23,958,233 × 5,000)
———————————————
139676498390 ( = 139,676,498,390 )
In some countries such as Germany, the above multiplication is depicted similarly but with the original product kept horizontal and computation starting with the first digit of the multiplier:[12]
23958233 · 5830
———————————————
119791165
191665864
71874699
00000000
———————————————
139676498390
Multiplying numbers to more than a couple of decimal places by hand is tedious and error-prone. Common logarithms were invented to simplify such calculations, since adding logarithms is equivalent to multiplying. The slide rule allowed numbers to be quickly multiplied to about three places of accuracy. Beginning in the early 20th century, mechanical calculators, such as the Marchant, automated multiplication of up to 10-digit numbers. Modern electronic computers and calculators have greatly reduced the need for multiplication by hand.
Historical algorithms
[edit]Methods of multiplication were documented in the writings of ancient Egyptian, Greek, Indian,[citation needed] and Chinese civilizations.
The Ishango bone, dated to about 18,000 to 20,000 BC, may hint at a knowledge of multiplication in the Upper Paleolithic era in Central Africa, but this is speculative.[13][verification needed]
Egyptians
[edit]The Egyptian method of multiplication of integers and fractions, which is documented in the Rhind Mathematical Papyrus, was by successive additions and doubling. For instance, to find the product of 13 and 21 one had to double 21 three times, obtaining 2 × 21 = 42, 4 × 21 = 2 × 42 = 84, 8 × 21 = 2 × 84 = 168. The full product could then be found by adding the appropriate terms found in the doubling sequence:[14]
- 13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273.
Babylonians
[edit]The Babylonians used a sexagesimal positional number system, analogous to the modern-day decimal system. Thus, Babylonian multiplication was very similar to modern decimal multiplication. Because of the relative difficulty of remembering 60 × 60 different products, Babylonian mathematicians employed multiplication tables. These tables consisted of a list of the first twenty multiples of a certain principal number n: n, 2n, ..., 20n; followed by the multiples of 10n: 30n 40n, and 50n. Then to compute any sexagesimal product, say 53n, one only needed to add 50n and 3n computed from the table.[citation needed]
Chinese
[edit]
In the mathematical text Zhoubi Suanjing, dated prior to 300 BC, and the Nine Chapters on the Mathematical Art, multiplication calculations were written out in words, although the early Chinese mathematicians employed Rod calculus involving place value addition, subtraction, multiplication, and division. The Chinese were already using a decimal multiplication table by the end of the Warring States period.[15]
Modern methods
[edit]
The modern method of multiplication based on the Hindu–Arabic numeral system was first described by Brahmagupta. Brahmagupta gave rules for addition, subtraction, multiplication, and division. Henry Burchard Fine, then a professor of mathematics at Princeton University, wrote the following:
- The Indians are the inventors not only of the positional decimal system itself, but of most of the processes involved in elementary reckoning with the system. Addition and subtraction they performed quite as they are performed nowadays; multiplication they effected in many ways, ours among them, but division they did cumbrously.[16]
These place value decimal arithmetic algorithms were introduced to Arab countries by Al Khwarizmi in the early 9th century and popularized in the Western world by Fibonacci in the 13th century.[17]
Grid method
[edit]Grid method multiplication, or the box method, is used in primary schools in England and Wales and in some areas[which?] of the United States to help teach an understanding of how multiple digit multiplication works. An example of multiplying 34 by 13 would be to lay the numbers out in a grid as follows:
× 30 4 10 300 40 3 90 12
and then add the entries.
Computer algorithms
[edit]The classical method of multiplying two n-digit numbers requires n2 digit multiplications. Multiplication algorithms have been designed that reduce the computation time considerably when multiplying large numbers. Methods based on the discrete Fourier transform reduce the computational complexity to O(n log n log log n). In 2016, the factor log log n was replaced by a function that increases much slower, though still not constant.[18] In March 2019, David Harvey and Joris van der Hoeven submitted a paper presenting an integer multiplication algorithm with a complexity of [19] The algorithm, also based on the fast Fourier transform, is conjectured to be asymptotically optimal.[20] The algorithm is not practically useful, as it only becomes faster for multiplying extremely large numbers (having more than 2172912 bits).[21]
Products of measurements
[edit]One can only meaningfully add or subtract quantities of the same type, but quantities of different types can be multiplied or divided without problems. For example, four bags with three marbles each can be thought of as:[1]
- [4 bags] × [3 marbles per bag] = 12 marbles.
When two measurements are multiplied together, the product is of a type depending on the types of measurements. The general theory is given by dimensional analysis. This analysis is routinely applied in physics, but it also has applications in finance and other applied fields.
A common example in physics is the fact that multiplying speed by time gives distance. For example:
- 50 kilometers per hour × 3 hours = 150 kilometers.
In this case, the hour units cancel out, leaving the product with only kilometer units.
Other examples of multiplication involving units include:
- 2.5 meters × 4.5 meters = 11.25 square meters
- 11 meters/seconds × 9 seconds = 99 meters
- 4.5 residents per house × 20 houses = 90 residents
Product of a sequence
[edit]Capital pi notation
[edit]The product of a sequence of factors can be written with the product symbol , which derives from the capital letter Π (pi) in the Greek alphabet (much like the same way the summation symbol is derived from the Greek letter Σ (sigma)).[22][23] The meaning of this notation is given by
which results in
In such a notation, the variable i represents a varying integer, called the multiplication index, that runs from the lower value 1 indicated in the subscript to the upper value 4 given by the superscript. The product is obtained by multiplying together all factors obtained by substituting the multiplication index for an integer between the lower and the upper values (the bounds included) in the expression that follows the product operator.
More generally, the notation is defined as
where m and n are integers or expressions that evaluate to integers. In the case where m = n, the value of the product is the same as that of the single factor xm; if m > n, the product is an empty product whose value is 1—regardless of the expression for the factors.
Properties of capital pi notation
[edit]By definition,
If all factors are identical, a product of n factors is equivalent to exponentiation:
Associativity and commutativity of multiplication imply
- and
if a is a non-negative integer, or if all are positive real numbers, and
if all are non-negative integers, or if x is a positive real number.
Infinite products
[edit]One may also consider products of infinitely many terms; these are called infinite products. Notationally, this consists in replacing n above by the infinity symbol ∞. The product of such an infinite sequence is defined as the limit of the product of the first n terms, as n grows without bound. That is,
One can similarly replace m with negative infinity, and define:
provided both limits exist.[citation needed]
Exponentiation
[edit]When multiplication is repeated, the resulting operation is known as exponentiation. For instance, the product of three factors of two (2×2×2) is "two raised to the third power", and is denoted by 23, a two with a superscript three. In this example, the number two is the base, and three is the exponent.[24] In general, the exponent (or superscript) indicates how many times the base appears in the expression, so that the expression
indicates that n copies of the base a are to be multiplied together. This notation can be used whenever multiplication is known to be power associative.
Properties
[edit]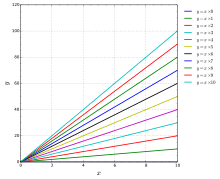
Extension of this pattern into other quadrants gives the reason why a negative number times a negative number yields a positive number.
Note also how multiplication by zero causes a reduction in dimensionality, as does multiplication by a singular matrix where the determinant is 0. In this process, information is lost and cannot be regained.
For real and complex numbers, which includes, for example, natural numbers, integers, and fractions, multiplication has certain properties:
- Commutative property
- The order in which two numbers are multiplied does not matter:[25][26]
- Associative property
- Expressions solely involving multiplication or addition are invariant with respect to the order of operations:[25][26]
- Distributive property
- Holds with respect to multiplication over addition. This identity is of prime importance in simplifying algebraic expressions:[25][26]
- Identity element
- The multiplicative identity is 1; anything multiplied by 1 is itself. This feature of 1 is known as the identity property:[25][26]
- Property of 0
- Any number multiplied by 0 is 0. This is known as the zero property of multiplication:[25]
- Negation
- −1 times any number is equal to the additive inverse of that number:
- , where
- −1 times −1 is 1:
- Inverse element
- Every number x, except 0, has a multiplicative inverse, , such that .[27]
- Order preservation
- Multiplication by a positive number preserves the order:
- For a > 0, if b > c, then ab > ac.
- Multiplication by a negative number reverses the order:
- For a < 0, if b > c, then ab < ac.
- The complex numbers do not have an ordering that is compatible with both addition and multiplication.[28]
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative for matrices and quaternions.[25]
Axioms
[edit]In the book Arithmetices principia, nova methodo exposita, Giuseppe Peano proposed axioms for arithmetic based on his axioms for natural numbers. Peano arithmetic has two axioms for multiplication:
Here S(y) represents the successor of y; i.e., the natural number that follows y. The various properties like associativity can be proved from these and the other axioms of Peano arithmetic, including induction. For instance, S(0), denoted by 1, is a multiplicative identity because
The axioms for integers typically define them as equivalence classes of ordered pairs of natural numbers. The model is based on treating (x,y) as equivalent to x − y when x and y are treated as integers. Thus both (0,1) and (1,2) are equivalent to −1. The multiplication axiom for integers defined this way is
The rule that −1 × −1 = 1 can then be deduced from
Multiplication is extended in a similar way to rational numbers and then to real numbers.[citation needed]
Multiplication with set theory
[edit]The product of non-negative integers can be defined with set theory using cardinal numbers or the Peano axioms. See below how to extend this to multiplying arbitrary integers, and then arbitrary rational numbers. The product of real numbers is defined in terms of products of rational numbers; see construction of the real numbers.[29]
Multiplication in group theory
[edit]There are many sets that, under the operation of multiplication, satisfy the axioms that define group structure. These axioms are closure, associativity, and the inclusion of an identity element and inverses.
A simple example is the set of non-zero rational numbers. Here identity 1 is had, as opposed to groups under addition where the identity is typically 0. Note that with the rationals, zero must be excluded because, under multiplication, it does not have an inverse: there is no rational number that can be multiplied by zero to result in 1. In this example, an abelian group is had, but that is not always the case.
To see this, consider the set of invertible square matrices of a given dimension over a given field. Here, it is straightforward to verify closure, associativity, and inclusion of identity (the identity matrix) and inverses. However, matrix multiplication is not commutative, which shows that this group is non-abelian.
Another fact worth noticing is that the integers under multiplication do not form a group—even if zero is excluded. This is easily seen by the nonexistence of an inverse for all elements other than 1 and −1.
Multiplication in group theory is typically notated either by a dot or by juxtaposition (the omission of an operation symbol between elements). So multiplying element a by element b could be notated as a b or ab. When referring to a group via the indication of the set and operation, the dot is used. For example, our first example could be indicated by .[30]
Multiplication of different kinds of numbers
[edit]Numbers can count (3 apples), order (the 3rd apple), or measure (3.5 feet high); as the history of mathematics has progressed from counting on our fingers to modelling quantum mechanics, multiplication has been generalized to more complicated and abstract types of numbers, and to things that are not numbers (such as matrices) or do not look much like numbers (such as quaternions).
- Integers
- is the sum of N copies of M when N and M are positive whole numbers. This gives the number of things in an array N wide and M high. Generalization to negative numbers can be done by
- and
- The same sign rules apply to rational and real numbers.
- Rational numbers
- Generalization to fractions is by multiplying the numerators and denominators, respectively: . This gives the area of a rectangle high and wide, and is the same as the number of things in an array when the rational numbers happen to be whole numbers.[25]
- Real numbers
- Real numbers and their products can be defined in terms of sequences of rational numbers.
- Complex numbers
- Considering complex numbers and as ordered pairs of real numbers and , the product is . This is the same as for reals when the imaginary parts and are zero.
- Equivalently, denoting as , [25]
- Alternatively, in trigonometric form, if , then[25]
- Further generalizations
- See Multiplication in group theory, above, and multiplicative group, which for example includes matrix multiplication. A very general, and abstract, concept of multiplication is as the "multiplicatively denoted" (second) binary operation in a ring. An example of a ring that is not any of the above number systems is a polynomial ring (polynomials can be added and multiplied, but polynomials are not numbers in any usual sense).
- Division
- Often division, , is the same as multiplication by an inverse, . Multiplication for some types of "numbers" may have corresponding division, without inverses; in an integral domain x may have no inverse "" but may be defined. In a division ring there are inverses, but may be ambiguous in non-commutative rings since need not be the same as .[citation needed]
See also
[edit]- Dimensional analysis
- Multiplication algorithm
- Karatsuba algorithm, for large numbers
- Toom–Cook multiplication, for very large numbers
- Schönhage–Strassen algorithm, for huge numbers
- Multiplication table
- Binary multiplier, how computers multiply
- Multiplicative inverse, reciprocal
- Factorial
- Genaille–Lucas rulers
- Lunar arithmetic
- Napier's bones
- Peasant multiplication
- Product (mathematics), for generalizations
- Slide rule
References
[edit]- ^ a b c Devlin, Keith (January 2011). "What Exactly is Multiplication?". Mathematical Association of America. Archived from the original on 2017-05-27. Retrieved 2017-05-14.
With multiplication you have a multiplicand (written second) multiplied by a multiplier (written first)
- ^ Khan Academy (2015-08-14), Intro to multiplication | Multiplication and division | Arithmetic | Khan Academy, archived from the original on 2017-03-24, retrieved 2017-03-07
- ^ Khan Academy (2012-09-06), Why aren't we using the multiplication sign? | Introduction to algebra | Algebra I | Khan Academy, archived from the original on 2017-03-27, retrieved 2017-03-07
- ^ "Victory on Points". Nature. 218 (5137): 111. 1968. Bibcode:1968Natur.218S.111.. doi:10.1038/218111c0.
- ^ "The Lancet – Formatting guidelines for electronic submission of manuscripts" (PDF). Retrieved 2017-04-25.
- ^ Announcing the TI Programmable 88! (PDF). Texas Instruments. 1982. Archived (PDF) from the original on 2017-08-03. Retrieved 2017-08-03.
Now, implied multiplication is recognized by the AOS and the square root, logarithmic, and trigonometric functions can be followed by their arguments as when working with pencil and paper.
(NB. The TI-88 only existed as a prototype and was never released to the public.) - ^ Peterson, Dave (2019-10-14). "Order of Operations: Implicit Multiplication?". Algebra / PEMDAS. The Math Doctors. Archived from the original on 2023-09-24. Retrieved 2023-09-25.
- ^ Peterson, Dave (2023-08-18). "Implied Multiplication 1: Not as Bad as You Think". Algebra / Ambiguity, PEMDAS. The Math Doctors. Archived from the original on 2023-09-24. Retrieved 2023-09-25; Peterson, Dave (2023-08-25). "Implied Multiplication 2: Is There a Standard?". Algebra, Arithmetic / Ambiguity, PEMDAS. The Math Doctors. Archived from the original on 2023-09-24. Retrieved 2023-09-25; Peterson, Dave (2023-09-01). "Implied Multiplication 3: You Can't Prove It". Algebra / PEMDAS. The Math Doctors. Archived from the original on 2023-09-24. Retrieved 2023-09-25.
- ^ Fuller, William R. (1977). FORTRAN Programming: A Supplement for Calculus Courses. Universitext. Springer. p. 10. doi:10.1007/978-1-4612-9938-7. ISBN 978-0-387-90283-8.
- ^ Ramone, Crewton. "Multiplicand and Multiplier". Crewton Ramone's House of Math. Archived from the original on 2015-10-26. Retrieved 2015-11-10..
- ^ Litvin, Chester (2012). Advance Brain Stimulation by Psychoconduction. Trafford. pp. 2–3, 5–6. ISBN 978-1-4669-0152-0 – via Google Book Search.
- ^ "Multiplication". mathematische-basteleien.de. Retrieved 2022-03-15.
- ^ Pletser, Vladimir (2012-04-04). "Does the Ishango Bone Indicate Knowledge of the Base 12? An Interpretation of a Prehistoric Discovery, the First Mathematical Tool of Humankind". arXiv:1204.1019 [math.HO].
- ^ "Peasant Multiplication". cut-the-knot.org. Retrieved 2021-12-29.
- ^ Qiu, Jane (2014-01-07). "Ancient times table hidden in Chinese bamboo strips". Nature. doi:10.1038/nature.2014.14482. S2CID 130132289. Archived from the original on 2014-01-22. Retrieved 2014-01-22.
- ^ Fine, Henry B. (1907). The Number System of Algebra – Treated Theoretically and Historically (PDF) (2nd ed.). p. 90.
- ^ Bernhard, Adrienne. "How modern mathematics emerged from a lost Islamic library". bbc.com. Retrieved 2022-04-22.
- ^ Harvey, David; van der Hoeven, Joris; Lecerf, Grégoire (2016). "Even faster integer multiplication". Journal of Complexity. 36: 1–30. arXiv:1407.3360. doi:10.1016/j.jco.2016.03.001. ISSN 0885-064X. S2CID 205861906.
- ^ David Harvey, Joris Van Der Hoeven (2019). Integer multiplication in time O(n log n) Archived 2019-04-08 at the Wayback Machine
- ^ Hartnett, Kevin (2019-04-11). "Mathematicians Discover the Perfect Way to Multiply". Quanta Magazine. Retrieved 2020-01-25.
- ^ Klarreich, Erica. "Multiplication Hits the Speed Limit". cacm.acm.org. Archived from the original on 2020-10-31. Retrieved 2020-01-25.
- ^ Weisstein, Eric W. "Product". mathworld.wolfram.com. Retrieved 2020-08-16.
- ^ "Summation and Product Notation". math.illinoisstate.edu. Retrieved 2020-08-16.
- ^ Weisstein, Eric W. "Exponentiation". mathworld.wolfram.com. Retrieved 2021-12-29.
- ^ a b c d e f g h i "Multiplication". Encyclopedia of Mathematics. Retrieved 2021-12-29.
- ^ a b c d Biggs, Norman L. (2002). Discrete Mathematics. Oxford University Press. p. 25. ISBN 978-0-19-871369-2.
- ^ Weisstein, Eric W. "Multiplicative Inverse". Wolfram MathWorld. Retrieved 2022-04-19.
- ^ Angell, David. "ORDERING COMPLEX NUMBERS... NOT*" (PDF). UNSW Sydney, School of Mathematics and Statistics. Retrieved 2021-12-29.
- ^ "10.2: Building the Real Numbers". Mathematics LibreTexts. 2018-04-11. Retrieved 2023-06-23.
- ^ Burns, Gerald (1977). Introduction to group theory with applications. New York: Academic Press. ISBN 9780121457501.
Further reading
[edit]- Boyer, Carl B. (revised by Merzbach, Uta C.) (1991). History of Mathematics. John Wiley and Sons, Inc. ISBN 978-0-471-54397-8.
((cite book)): CS1 maint: multiple names: authors list (link)
External links
[edit]- Multiplication and Arithmetic Operations In Various Number Systems at cut-the-knot
- Modern Chinese Multiplication Techniques on an Abacus
| Primary | |
|---|---|
| Inverse for left argument | |
| Inverse for right argument | |
| Related articles | |






![{\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividend))}{\scriptstyle {\text{divisor))))\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerator))}{\scriptstyle {\text{denominator))))\end{matrix))\right\}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5d22ff59234f0d437be740306e8dd905991e1e)



![{\displaystyle \scriptstyle {\sqrt[{\text{degree))]{\scriptstyle {\text{radicand))))\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)
































































































