The International System of Units (abbreviated as SI, from the French Système international (d'unités)) is the modern form of the metric system, and is the most widely used system of measurement. It comprises a coherent system of units of measurement built on seven base units (ampere, kelvin, second, metre, kilogram, candela, mole) and a set of twenty decimal prefixes to the unit names and unit symbols that may be used when specifying multiples and fractions of the units. The system also specifies names for 22 derived units for other common physical quantities like lumen, watt, etc.

The base units, except for one, are derived from invariant constants of nature, such as the speed of light and triple point of water, which can be readily observed and measured with great accuracy. The kilogram standard of mass is a physical artefact certified in 1889, consisting of a cylinder of platinum-iridium which ostensibly was the same mass (weight) as one litre of water at the freezing point. Its stability has been a matter of significant concern, resulting in recent proposals to change the definition to one derived from some invariant constant of nature.^[1]

The derived units may be defined in terms of base units and/or other derived units in arbitrary combinations. They are adopted to facilitate measurement in diverse fields of endeavor. SI is intended to be an evolving system, so prefixes and units are created and unit definitions are modified through international agreement as the technology of measurement progresses and the precision of measurements improves. The last new derived unit was defined in 1999.

The reliability of the SI system depends not only on the precise measurement of standards for the base units in terms of various physical constants of nature, but also on precise determination of those constants. The set of constants used periodically changes as more stable constants are found, or ones which may be more precisely measured. One significant consequence is that in 1983, the meter was defined to be the distance that light travels in a vacuum for an exact but minute fraction of a second (about a 300 millionth) so that the speed of light is now an exactly defined constant of nature^[2], and will not change.

The motivation for the development of the SI was the diversity of units that had sprung up within the centimetre–gram–second (CGS) systems (specifically the inconsistency between the systems of electrostatic units and electromagnetic units) and the lack of coordination between the various disciplines that used them. The General Conference on Weights and Measures (French: Conférence générale des poids et mesures – CGPM), which was established by the Metre Convention of 1875, brought together many international organisations to establish the definitions and standards of a new system and standardise the rules for writing and presenting measurements. The system was published in 1960 as a result of an initiative that began in 1948. It is based on the metre–kilogram–second system of units (MKS) rather than any variant of the CGS. Since then, the SI has been adopted by all developed countries except the United States.^[3]

The International System of Units consists of a set of base units, a set of coherent derived units, and a set of decimal-based multipliers that are used as prefixes.^{[4]: 103–106} Coherent units are derived units that contain no numerical factor other than 1—quantities such as standard gravity and density of water are absent from their definitions. In the example above, one newton is the force required to accelerate a mass of one kilogram by one metre per second squared. Since the SI units of mass and acceleration are kg and m·s⁻² respectively and F ∝ m × a, the units of force (and hence of newtons) is formed by multiplication to give kg·m·s⁻². Since the newton is part of a coherent set of units, the constant of proportionality is 1.

While the base and specified derived units are coherent, they are not necessarily independent or disjoint: for example, anything that could be specified in terms of siemens, could just as well be specified in terms of ohms, because ohms and siemens are inverses of each other. And both ohms and siemens could be replaced with a combination of amperes and volts, because those quantities bear a defined relationship to each other^[5].

The SI base units are the building blocks of the system and all other units are derived from them. When Maxwell first introduced the concept of a coherent system, he identified three quantities that could be used as base units: mass, length and time. Giorgi later identified the need for an electrical base unit. Theoretically any one of electric current, potential difference, electrical resistance, electrical charge or a number of other quantities could have provided the base unit, with the remaining units then being defined by the laws of physics. In the event, the unit of electric current was chosen for SI. Another three base units (for temperature, substance and luminous intensity) were added later.

The derived units in the SI are formed by powers, products or quotients of the base units and are unlimited in number.^{[4]: 103 [6]: 3} Derived units are associated with derived quantities, for example velocity is a quantity that is derived from the base quantities of time and length, so in SI the derived unit is metres per second (symbol m/s). The dimensions of derived units can be expressed in terms of the dimensions of the base units.

Derived units may themselves be used in combination with the names and symbols for base units and for other derived units to express the units of other derived quantities. For example, the SI unit of force is the newton (N), the SI unit of pressure is the pascal (Pa)—and the pascal can be defined as one newton per square metre (N/m²).^[12]

Prefixes are added to unit names to produce multiple and sub-multiples of the original unit. All multiples are integer powers of ten, and above a hundred or below a hundredth all are integer powers of a thousand. For example, kilo- denotes a multiple of a thousand and milli- denotes a multiple of a thousandth, so there are one thousand millimetres to the metre and one thousand metres to the kilometre. The prefixes are never combined, so for example a millionth of a metre is a micrometre, not a millimillimetre. Multiples of the kilogram are named as if the gram were the base unit, so a millionth of a kilogram is a milligram, not a microkilogram.^{[4]: 122 [13]: 14}

The SI is capable of describing any measurable physical quantity^{[citation needed]}, but many non-SI units still appear in the scientific, technical, and commercial literature, and will continue to be used for many years. Some units are so deeply embedded in history and many cultures that they will continue to be used for the foreseeable future. The CIPM recognised and acknowledged such traditions by compiling a list of non-SI units accepted for use with SI, which are grouped as follows:^{[4]: 123–129 [13]: 7–11 [Note 1]}

• Non-SI units accepted for use with the SI:

Certain units of time, angle, and legacy non-SI metric units have a long history of consistent use. Most societies have used the solar day and its non-decimal subdivisions as a basis of time and, unlike the foot or the pound, these were the same regardless of where they were being measured. The radian, being ⁠1/2π⁠ of a revolution, has mathematical advantages but it is cumbersome for navigation, and, as with time, the units used in navigation have a large degree of consistency around the world. The tonne, litre, and hectare were adopted by the CGPM in 1879 and have been retained as units that may be used alongside SI units, having been given unique symbols. The catalogued units are

minute, hour, day, degree of arc, minute of arc, second of arc, hectare, litre, tonne, astronomical unit and [deci]bel

• Non-SI units whose values in SI units must be obtained experimentally (Table 7).

Physicists often use units of measure that are based on natural phenomena, particularly when the quantities associated with these phenomena are many orders of magnitude greater than or less than the equivalent SI unit. The most common ones have been catalogued in the SI Brochure together with consistent symbols and accepted values, but with the caveat that their values in SI units need to be measured.^{[Note 2]}

electronvolt (symbol eV), and dalton/unified atomic mass unit (Da or u)

• Other non-SI units (Table 8):

A number of non-SI units that had never been formally sanctioned by the CGPM have continued to be used across the globe in many spheres including health care and navigation. As with the units of measure in Tables 6 and 7, these have been catalogued by the CIPM in the SI Brochure to ensure consistent usage, but with the recommendation that authors who use them should define them wherever they are used.

bar, millimetre of mercury, ångström, nautical mile, barn, knot and neper

In the interests of standardising health-related units of measure used in the nuclear industry, the 12th CGPM (1964) accepted the continued use of the curie (symbol Ci) as a non-SI unit of activity for radionuclides;^[4]: 152 the becquerel, sievert and gray were adopted in later years. Similarly, the millimetre of mercury (symbol mmHg) was retained for measuring blood pressure.^[4]: 127

• Non-SI units associated with the CGS and the CGS-Gaussian system of units (Table 9)

The SI manual also catalogues a number of legacy units of measure that are used in specific fields such as geodesy and geophysics or are found in the literature, particularly in classical and relativistic electrodynamics where they have certain advantages: The units that are catalogued are:

erg, dyne, poise, stokes, stilb, phot, gal, maxwell, gauss, and oersted.

The basic units of the metric system as originally defined represented common quantities or relationships in nature, ones that could be easily observed and accurately measured. They still do - the modern precisely defined quantities are refinements of methodology, not changes in magnitude. In cases where laboratory precision may not be required or available, or approximations are good enough, the original quantities or multiples or fractions of them are often readily available.

• The kilogram is the weight of a litre of cold water; a cubic centimetre or millilitre of water weighs a gram (we need not be too concerned about the difference between mass and weight); a 1-Euro coin 7.5g; a Sacagawea 1 US dollar coin, 8.1g; a UK 50 pence coin, 8.0g.
• The metre is the length of a pendulum of period 2 seconds; most dining tabletops are about 0.75 metre high; a very tall human (basketball forward) is about 2 metres tall.
• A second is a 60th of a minute, which is a 60th of an hour, which is a 24th of a day, so a second is 1/86400 of a day; a second is the time it takes a small dense object to fall 4.9 metres from rest.
• A candela is about the luminous intensity of a moderately bright candle, or 1 candle power; a 60 W tungsten incandescent light bulb is about 64 candle power.
• A mole of a substance is its molecular weight expressed in units of grams; a mole of table salt is 58.4 g.
• A degree Kelvin is the same as a degree centigrade: 1/100 of the temperature differential between the freezing and boiling points of water at sea level; Kelvin temperature is centigrade temperature plus about 273; human body temperature is about 37°C or 310 K.
• A 60W incandescent light bulb consumes about 0.5 amperes at 120 V (US mains voltage) and a little more than 0.25 amperes at 220V (European mains voltage).

The quantities and equations that define the SI units are now referred to as the International System of Quantities (ISQ). The system is based on seven base quantities: length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity. Other quantities such as area, pressure, and electrical resistance are derived from these base quantities by clear non-contradictory equations. The ISQ defines the quantities that are measured with the SI units.^[16] The ISQ is defined in the international standard ISO/IEC 80000, and was finalised in 2009 with the publication of ISO 80000-1.^[17]

Metrologists carefully distinguish between the definition of a unit and its realisation. The definition of each base unit of the SI is drawn up so that it is unique and provides a sound theoretical basis on which the most accurate and reproducible measurements can be made. The realisation of the definition of a unit is the procedure by which the definition may be used to establish the value and associated uncertainty of a quantity of the same kind as the unit. A description of the mise en pratique^{[Note 3]} of the base units is given in an electronic appendix to the SI Brochure.^{[19][4]: 168–169}

The published mise en pratique is not the only way in which a base unit can be determined: the SI Brochure states that "any method consistent with the laws of physics could be used to realise any SI unit."^[4]: 111 In the current (2016) exercise to overhaul the definitions of the base units, various consultative committees of the CIPM have required that more than one mise en pratique shall be developed for determining the value of each unit.^{[citation needed]} In particular:

• At least three separate experiments be carried out yielding values having a relative standard uncertainty in the determination of the kilogram of no more than 5×10⁻⁸ and at least one of these values should be better than 2×10⁻⁸. Both the Watt balance and the Avogadro project should be included in the experiments and any differences between these be reconciled.^[20][21]
• When the kelvin is being determined, the relative uncertainty of the Boltzmann constant derived from two fundamentally different methods such as acoustic gas thermometry and dielectric constant gas thermometry be better than one part in 10⁻⁶ and that these values be corroborated by other measurements.^[22]

The first version of the metric system was devised and implemented during the French Revolution (1790s) with just the metre and kilogram as standards of length and weight respectively. In the 1830s Carl Friedrich Gauss laid the foundations for a coherent system based on length, mass, and time.^{[Note 4]} In the 1860s a group working under the auspices of the British Association for the Advancement of Science formulated the requirement for a coherent system of units with base units and derived units. The inclusion of electrical units into the system was hampered by the customary use of more than one set of units, until 1900 when Giovanni Giorgi identified the need to define one single electrical quantity as a fourth base quantity alongside the original three base quantities.

Meanwhile, in 1875, the Treaty of the Metre passed responsibility for verification of the kilogram and metre against agreed prototypes from French to international control. In 1921, the Treaty was extended to include all physical quantities including electrical units originally defined in 1893.

In 1948, an overhaul of the metric system was set in motion which resulted in the development of the "Practical system of units" which, on its publication in 1960, was given the name "The International System of Units". In 1954, the 10th General Conference on Weights and Measures (CGPM) identified electric current as the fourth base quantity in the practical system of units and added two more base quantities ( —temperature and luminous intensity) making six base quantities in all. The units associated with these quantities were the metre, kilogram, second, ampere, kelvin and candela. In 1971, a seventh base quantity, amount of substance represented by the mole, was added to the definition of SI.

The metric system was developed from 1791 onwards by a committee of the French Academy of Sciences, commissioned by the National Assembly and Louis XVI to create a unified and rational system of measures.^[25] The group, which included Antoine Lavoisier (the "father of modern chemistry") and the mathematicians Pierre-Simon Laplace and Adrien-Marie Legendre,^[26]: 89 used the same principles for relating length, volume, and mass that had been proposed by the English clergyman John Wilkins in 1668^[27][28] and the concept of using the Earth's meridian as the basis of the definition of length, originally proposed in 1670 by the French abbot Mouton.^[29][30]

On 30 March 1791, the Assembly adopted the committee's proposed principles for the new decimal system of measure and authorised a survey between Dunkirk and Barcelona to establish the length of the meridian. On 11 July 1792, the committee proposed the names metre, are, litre and grave for the units of length, area, capacity, and mass, respectively. The committee also proposed that multiples and submultiples of these units were to be denoted by decimal-based prefixes such as centi for a hundredth and kilo for a thousand.^[31]: 82

Thomson

Maxwell

William Thomson (Lord Kelvin) and James Clerk Maxwell played a prominent role in the development of the principle of coherence and in the naming of many units of measure.^{[32][33][34][35][36]}

The law of 7 April 1795 (loi du 18 germinal) defined the terms gramme and kilogramme, which replaced the former terms gravet (correctly^{[dubious – discuss]} milligrave) and grave, and on 22 June 1799 (after Pierre Méchain and Jean-Baptiste Delambre had completed the meridian survey) the definitive standard mètre des Archives and kilogramme des Archives were deposited in the French National Archives. On 10 December 1799, the law by which the metric system was to be definitively adopted in France (loi du 19 frimaire^[37]) was passed.^[38]

During the first half of the 19th century there was little consistency in the choice of preferred multiples of the base units: typically the myriametre (10000 metres) was in widespread use in both France and parts of Germany, while the kilogram (1000 grams) rather than the myriagram was used for mass.^[23]

In 1832, the German mathematician Carl Friedrich Gauss, assisted by Wilhelm Weber, implicitly defined the second as a base unit when he quoted the Earth's magnetic field in terms of millimetres, grams, and seconds.^[32] Prior to this, the strength of the Earth's magnetic field had only been described in relative terms. The technique used by Gauss was to equate the torque induced on a suspended magnet of known mass by the Earth's magnetic field with the torque induced on an equivalent system under gravity. The resultant calculations enabled him to assign dimensions based on mass, length and time to the magnetic field.^[39]

In the 1860s, James Clerk Maxwell, William Thomson (later Lord Kelvin) and others working under the auspices of the British Association for the Advancement of Science, built on Gauss' work and formalised the concept of a coherent system of units with base units and derived units. The principle of coherence was successfully used to define a number of units of measure based on the centimetre–gram–second system of units (CGS), including the erg for energy, the dyne for force, the barye for pressure, the poise for dynamic viscosity and the stokes for kinematic viscosity.^[35]

A French-inspired initiative for international cooperation in metrology led to the signing in 1875 of the Metre Convention.^{[26]: 353–354} Initially the convention only covered standards for the metre and the kilogram. A set of 30 prototypes of the metre and 40 prototypes of the kilogram,^{[Note 6]} in each case made of a 90% platinum-10% iridium alloy, were manufactured by the British firm Johnson, Matthey & Co and accepted by the CGPM in 1889. One of each was selected at random to become the International prototype metre and International prototype kilogram that replaced the mètre des Archives and kilogramme des Archives respectively. Each member state was entitled to one of each of the remaining prototypes to serve as the national prototype for that country.^[40]

The treaty established three international organisations to oversee the keeping of international standards of measurement:^[41]

• General Conference on Weights and Measures (Conférence générale des poids et mesures or CGPM) – a meeting every four to six years of delegates from all member states that receives and discusses a report from the CIPM and that endorses new developments in the SI on the advice of the CIPM.
• International Committee for Weights and Measures (Comité international des poids et mesures or CIPM) – a committee that meets annually at the BIPM and is made up of eighteen individuals of high scientific standing, nominated by the CGPM to advise the CGPM on administrative and technical matters
• International Bureau of Weights and Measures (Bureau international des poids et mesures or BIPM) – an international metrology centre at Sèvres in France that has custody of the International prototype kilogram, provides metrology services for the CGPM and CIPM, houses the secretariat for these organisations and hosts their formal meetings. Initially its prime metrological purpose was a periodic recalibration of national prototype metres and kilograms against the international prototype.

In 1921, the Metre Convention was extended to include all physical units, including the ampere and others defined by the Fourth International Conference of Electricians in Chicago in 1893, thereby enabling the CGPM to address inconsistencies in the way that the metric system had been used.^{[33][4]: 96}

At the close of the 19th century three different systems of units of measure existed for electrical measurements: a CGS-based system for electrostatic units, also known as the Gaussian or ESU system, a CGS-based system for electromechanical units (EMU) and an MKS-based system ("international system")^[42] for electrical distribution systems. Attempts to resolve the electrical units in terms of length, mass, and time using dimensional analysis was beset with difficulties—the dimensions depended on whether one used the ESU or EMU systems.^[36] This anomaly was resolved in 1900 when Giovanni Giorgi published a paper in which he advocated using a fourth base unit alongside the existing three base units. The fourth unit could be chosen to be electric current, voltage, or electrical resistance.^[43]

In the late 19th and early 20th centuries, a number of non-coherent units of measure based on the gram/kilogram, the centimetre/metre, and the second, such as the Pferdestärke (metric horsepower) for power,^{[44][Note 7]} the darcy for permeability^[45] and the use of "millimetres of mercury" for the measurement of both barometric and blood pressure were developed or propagated, some of which incorporated standard gravity in their definitions.

At the end of the Second World War, a number of different systems of measurement were in use throughout the world. Some of these systems were metric system variations, whereas others were based on customary systems of measure. In 1948, after representations by the International Union of Pure and Applied Physics (IUPAP) and by the French Government, the 9th General Conference on Weights and Measures (CGPM) asked the International Committee for Weights and Measures (CIPM) to conduct an international study of the measurement needs of the scientific, technical, and educational communities and "to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention".^[46]

On the basis of the findings of this study, the 10th CGPM in 1954 decided that an international system should be derived from six base units to provide for the measurement of temperature and optical radiation in addition to mechanical and electromagnetic quantities. Six base units were recommended: the metre, kilogram, second, ampere, degree Kelvin (later renamed kelvin), and candela.

In 1960, the 11th CGPM named the system the International System of Units, abbreviated SI from the French name, [Le Système International d'Unités] Error: ((Lang)): text has italic markup (help).^{[4]: 110 [47]}

The BIPM has described SI as "the modern metric system".^[4]: 95 Changing technology has led to an evolution of the definitions and standards that has followed two principal strands – changes to SI itself, and clarification of how to use units of measure that are not part of SI but are still nevertheless used on a worldwide basis. Since 1960 the CGPM has made a number of changes to SI. These include:

• The 12th CGPM (1964) extended the original SI-defined prefixes ranging from pico- (10⁻¹²) to tera- (10¹²).^[4]: 152 They were again extended at the 15th CGPM (1975)^[4]: 158 and the 19th CGPM (1991)^[4]: 164 to give the current range of prefixes, 10^-24 to 10²⁴.
• The 13th CGPM (1967) renamed the "degree Kelvin" (symbol °K) to the "kelvin" (symbol K)^[4]: 156
• The 14th CGPM (1971) added the mole (symbol mol) for an amount of substance, the pascal (symbol Pa) for pressure and the siemens (symbol S) for electrical conductance to the list of named derived units.^{[4]: 156 [48]}
• The 15th CGPM (1975) added the becquerel (symbol Bq) for "activity referred to a radionuclide" and the gray (symbol Gy) for ionizing radiation to the list of named derived units^[4]: 156
• The 16th CGPM (1979) added the sievert (symbol Sv) to the list of named derived units as the unit of dose equivalent.^[4]: 158 in order to distinguish between "absorbed dose" and "dose equivalent"; it also clarified that a capital "L" may be used as a symbol for the litre, in order to avoid confusion between the lower-case letter and the digit one.^[4]: 159

• The 17th CGPM (1983) replaced the definition of the standard metre with the distance that light travels in a vacuum in exactly ⁠1/299792458⁠ second, so that the speed of light is now a specified constant of nature.
• The 21st CGPM (1999) added the katal (symbol kat) for catalytic activity to the list of named derived units.^[4]: 165

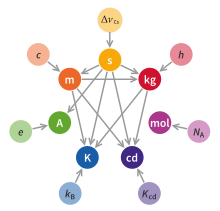
After the metre was redefined in 1960, the kilogram remained the only SI base unit that relied on a specific physical artefact, the international prototype of the kilogram (IPK), for its definition and thus the only unit that was still subject to periodic comparisons of national standard kilograms with the IPK.^[49] During the 2nd and 3rd Periodic Verification of National Prototypes of the Kilogram, a significant divergence in weight between the IPK and all of its official copies stored around the world had occurred: the copies had all gained noticeable weight with respect to the IPK. During extraordinary verifications carried out in 2014 preparatory to redefinition of metric standards, continuing divergence was not confirmed. Nonetheless, the residual and irreducible instability of a physical IPK undermines the reliability of the entire metric system to precision measurement from small (atomic) to large (astrophysical) scales.

At its 23rd meeting, held in 2007, the CGPM recommended that the CIPM should continue to investigate methods to provide exact fixed values for physical constants of nature that could then be used in the definitions of units of measure in place of the IPK, thus enabling the transition from explicit unit definitions to explicit constant definitions.^[50][51]

At a meeting of the CCU held in Reading, United Kingdom, in September 2010, a resolution and draft changes to the SI Brochure that were to be presented to the next meeting of the CIPM in October 2010 were agreed to in principle.^[52][53] The proposals that the CCU put forward were:

• In addition to the speed of light, four constants of nature – the Planck constant, an elementary charge, the Boltzmann constant and the Avogadro number – be defined to have exact values.
• The International prototype kilogram be retired
• The current definitions of the kilogram, ampere, kelvin and mole be revised.
• The wording of the definitions of all the base units be both tightened up and changed to reflect the change in emphasis from explicit unit to explicit constant definitions.

The CIPM meeting of October 2010 reviewed progress towards establishing fixed values for the constants but found that "the conditions set by the General Conference at its 23rd meeting have not yet been fully met. For this reason the CIPM does not propose a revision of the SI at the present time".^[54]

At the 24th CGPM meeting, held in October 2011, the CIPM sponsored a resolution in which the requisite definition changes were agreed to in principle and in which the conditions required to be met before the redefinitions could be implemented were restated.^[55]

By November 2014 the conditions set out at the 23rd meeting of the CGPM for the unit redefinitions had still not been met, and the 25th meeting of the CGPM, held in November 2014, adopted a similar resolution encouraging further work towards establishing fixed values for the fundamental constants.^[56]

The redefinitions are expected to be adopted at the 26th CGPM in November 2018.^[57] The CODATA task group on fundamental constants has announced special submission deadlines for data to compute the values that will be announced at this event.^[58]

Top view of the 2 kg weight (with a credit card to show the weight's size)

Bottom view of the 2 kg showing the lead plug and assayer's stamp.

A commercial-quality hexagonal 2 kg weight with a lead plug and assayer's mark and year of manufacture ("79" representing "1979") that is similar to, but which predates OIML recommendation R52.^[59]

SI has become the world's most widely used system of measurement, used in both everyday commerce and science.^[60][61] The change to SI had little effect on everyday life in countries that used the metric system – the metre, kilogram, litre and second remained unchanged as did the way in which they were used – most of the changes only affected measurements in the workplace.^[62] The CGPM has a role of recommending changes, but no formal role in the enforcement of such changes—another inter-governmental organisation, the International Organization of Legal Metrology (OIML) provides a forum for harmonisation of national standards and legislation in respect of metrology.

Both the degree and rate of adoption of SI varied from country to country—countries that had not adopted the metric system by 1960 and subsequently adopted SI did so directly as part of their metrication programs while others migrated from the CGS system of units to SI. In 1960, the world's largest economy was that of the United States, followed by the Soviet Union, West Germany, France, Japan, China and India.^[63] The United States and the United Kingdom were non-metric, Soviet Union was metric, France and Germany had been using the metric system for about a century, and China had been using the metric system for 35 years, while India and Japan had adopted the metric system within the preceding five years. Other non-metric countries were those where the United Kingdom or the United States had considerable influence.^{[Note 8][64]} These differences are brought out in the examples below:

Even though the use of metric units was legalised for trade in the UK in 1864, the UK had signed the Metre Convention in 1884 and the UK Parliament had defined the yard and the pound in terms of the metre and the kilogram in 1897, the UK continued to use the imperial system of measure^[65] and to export the imperial system of units to the Empire. In 1932, the system of Imperial Preference was set up at the Ottawa Conference. Although Ireland left the Commonwealth in 1948 and South Africa in 1961,^[66] both continued their close economic ties with the Commonwealth.^[67]

When the SI standard was published in 1960, the only major Commonwealth country to have adopted the metric system was India. In 1863, the first reading of a bill that would have made the metric system compulsory passed its first reading in the House of Commons by 110 votes to 75. The bill, however, failed to make the statute book because of lack of parliamentary time.^[31]: 136 In 1965, after this and similar false starts the then Federation of British Industry informed the British Government that its members favoured the adoption of the metric system. The rationale behind the request was that 80% of British exports were to countries that used the metric system or that were considering changing to the metric system. The Board of Trade, on behalf of the Government, agreed to support a ten-year metrication programme. The government agreed to a voluntary policy requiring minimal legislation and costs to be borne where they fell. SI would be used from the outset.^[68] The rest of the Commonwealth, South Africa and Ireland followed within a few years; in some countries such as South Africa and Australia metrication was mandatory rather than voluntary.^[69][70]

By 1980 all apart from the United Kingdom, Canada and Ireland had effectively completed their programs. In the United Kingdom the breakdown of voluntary metrication in the mid-1970s^{[71]: §1.8} coincided with the United Kingdom's obligations as part of the EEC to adopt the metric system, resulting in legislation to force metrication in certain areas and the Eurosceptic movement adopting an anti-metrication stance and the United Kingdom seeking a number of derogations from the relevant EEC directives. Once the metrication of most consumer goods was completed in 2000, aspects of British life, especially in government, commerce and industry used SI.^{[71]: §1.6 & §1.10} Although imperial units are widely encountered in unregulated areas such as the press and everyday speech, SI or units approved for use alongside SI are used in most areas where units of measure are regulated. High-profile exceptions include the sale of draught beer, the sale of milk in returnable containers, and United Kingdom road signs. Irish road signs (road distances and speeds) were converted to metric units during the first decade of the 21st century;^[72] otherwise, the situation in Ireland is similar to that in the United Kingdom.^[73]

Canada has adopted it for most purposes, but imperial units are still legally permitted and remain in common use throughout a few sectors of Canadian society, particularly in the buildings, trades and railways sectors.^[74][75]

In 1960, all the largest industrialised nations that had an established history of using the metric system were members of the European Economic Community (EEC).

In 1972, in order to harmonise units of measure as part of a programme to facilitate trade between member states, the EEC issued directive 71/354/EEC.^[76] This directive catalogued units of measure that could be used for "economic, public health, public safety and administrative purposes" and also provided instructions for a transition from the existing units of measure that were in use. The directive replicated the CGPM SI recommendations and in addition pre-empted some of the additions whose use had been recommended by the CIPM in 1969, but had not been ratified by the CGPM.^{[Note 9]} The directive also catalogued units of measure whose status would be reviewed by the end of 1977 (mainly coherent CGS units of measure) and also catalogued units of measure that were to be phased out by the end of 1977, including the use of obsolete names for the sale of timber such as the stere, the use of units of force and pressure that made use of the acceleration due to gravity,^{[Note 10]} the use of non-coherent units of power such as the Pferdestärke (PS), the use of the calorie as a measure of energy and the stilb as a measure of luminance. The directive was silent in respect of units that were specific to one or two countries including the pond, pfund, livre (Dutch, German and French synonyms for 500 g), thereby effectively prohibiting their use as well.

When the directive was revisited during 1977, some of the older units that were being reviewed (such as millimetre of mercury for blood pressure)^{[Note 11]} were retained but others were phased out, thereby broadly aligning the allowable units with SI. The directive was however overhauled to accommodate British and Irish interests in retaining the imperial system in certain circumstances.^[77] It was reissued as directive 80/181/EEC. During subsequent revisions, the directive has reflected changes in the definition of SI. The directive also formalised the use of supplementary units, which in 1979 were permitted for a period of ten years. The cut-off date for the use of supplementary units was extended a number of times and in 2009 was extended indefinitely.^[78]

India was one of the last countries to start a metrication programme before the advent of SI. When it became independent in 1947, both imperial and native units of measure were in use. Its metrication programme started in 1956 with the passing of the Standards of Weights and Measures Act. Part of the act fixed the value of the seer (a legacy unit of mass) to 0.9331 kg exactly; elsewhere the Act declared that from 1960 all non-metric units of measure were to be illegal.^[80]

Four years after the Indian Government announced its metrication programme, SI was published. The result was that the initial metrication programme was a conversion to the CGS system of units and the subsequent adoption of SI has been haphazard. Originally the Indian Government had planned to replace all units of measure with metric units by 1960. In 1976 a new Weights and Measures Act replaced the 1956 Act which, amongst other things, required that all weighing devices be approved before being released onto the market place. However, in 2012, it was reported that traditional units were still encountered in small manufacturing establishments and in the marketplace alongside CGS, SI and imperial measures, particularly in the poorer areas.^[81]

The use of the Indian numbering system of crores (10000000) and lakhs (100000), which do not map onto the SI system of prefixes, is widespread and is often found alongside or in place of the western numbering system.^[82]

Even though Congress set up a framework for the use of the metric system in the nineteenth century,^{[83][Note 12]} the United States continues to use US customary units, based on English measure passed by parliament under the reign of Queen Anne in 1706, for most purposes apart from science and medicine.^[84] In Puerto Rico, metric units are widely used due to its Spanish colonial history.^[85]

On 10 February 1964, the National Bureau of Standards (now the National Institute of Standards and Technology) issued a statement that it was to use SI except where this would have an obvious detrimental effect. In 1968 Congress authorised the U.S. Metric Study, the emphasis of which was to examine the feasibility of adopting SI.^[86] The first volume was delivered in 1970.^[87] The study recommended that the United States adopt the International System of units,^[88] and in 1975 Congress passed the Metric Conversion Act of 1975, which established a national policy of coordinating and planning for the increased use of the metric measurement system in the United States.^[89] Metrication was voluntary and to be coordinated by the United States Metric Board (USMB).^[90]

Efforts during the Ford and Carter administrations to force metrication were seized on by many newspaper editorialists as being dictatorial.^[26]: 365 Public response included resistance, apathy, and sometimes ridicule.^[91] The underlying reasons for this response include a relative uniformity of weights and measures (though, notably, US liquid measure differed by about 20% from British Imperial measure, which was adopted throughout the British Empire in 1824) inherited from the United Kingdom in 1776, a homogeneous economy and the influence of business groups and populists in Congress caused the country to look at the short-term costs associated with the change-over, particularly those that would be borne by the consumer rather than long-term benefits of efficiency and international trade. The Metrication Board was disbanded under President Ronald Reagan's direction in 1982.^{[26]: 362–365}

The 1988 Omnibus Foreign Trade and Competitiveness Act removed international trade barriers and amended the Metric Conversion Act of 1975, designating the metric system as "the Preferred system of weights and measures for United States trade and commerce". The legislation stated that the federal government has a responsibility to assist industry, especially small business, as it voluntarily converts to the metric system of measurement.^[92] Exceptions were made for the highway and construction industries; the Department of Transportation planned to require metric units by 2000, but this plan was cancelled by the 1998 highway bill TEA21.^[93] However, the US military uses the metric system widely, partly because of the need to work with armed services from other nations.^[94] Although overall responsibility for labelling requirements of consumer goods lies with Congress and is therefore covered by federal law, details of labelling requirements for certain commodities are controlled by state law or by other authorities such as the Food and Drug Administration, Environmental Protection Agency and Alcohol and Tobacco Tax and Trade Bureau.^[95] The federal Fair Packaging and Labeling Act (FPLA), originally passed in 1964, was amended in 1992 to require consumer goods directly under its jurisdiction to be labelled in both customary and metric units. Some industries are engaged in efforts to amend this law to allow manufacturers to use only metric labelling.^[96] The National Conference on Weights and Measures has developed the Uniform Packaging and Labeling Regulations (UPLR) which provides a standard approach to those sections of packaging law that are under state control. Acceptance of the UPLR varies from state to state – fourteen states accept it by merely citing it in their legislation.^[97]

During the first decade of the 21st century, the EU directive 80/181/EEC had required that dual unit labelling of goods sold within the EU cease by the end of 2009. This was backed up by requests from other nations including Japan and New Zealand to permit metric-only labelling as an aid to trade with those countries.^[95] Opinion in the United States was split – a bill to permit metric-only labelling at the federal level was to have been introduced in 2005 but significant opposition from the Food Marketing Institute, representing US grocers, has delayed the introduction of the bill. During a routine decennial review of the directive in 2008, the EU postponed the sunset clause for dual units indefinitely.

Meanwhile, in 1999 the UPLR was amended to permit metric-only labelling and automatically became law in those states that accept UPLR "as is". By 1 January 2009, 48 out of 50 states permit metric-only labelling, either through UPLR or through their own legislation.^[95] As of February 2013^[update] the use of metric (and therefore SI) units in the United States does not follow any pattern. Dual-unit labelling on consumer goods is mandatory. Some consumer goods such as soft drinks are sold in metric quantities, but milk is sold in customary units. The engineering industry is equally split. The automotive industry is largely metric,^[98] but aircraft such as the Boeing 787 Dreamliner were designed using customary units.^[99]

Before 1948, the use and representation of metric quantities was inconsistent and ambiguous.^{[citation needed]} In 1879, the CIPM published recommendations for writing the symbols for length, area, volume and mass, but it was outside its domain to publish recommendations for other quantities. Beginning in about 1900, physicists who had been using the symbol "μ"(mu) for "micrometre" or "micron", "λ"(lambda) for "microlitre", and "γ"(gamma) for "microgram" started to use the symbols "μm", "μL" and "μg", but it was only in 1935, a decade after the revision of the Metre Convention that the CIPM formally adopted this proposal and recommended that the symbol "μ" be used universally as a prefix for 10⁻⁶.^[100]

In 1948, the ninth CGPM approved the first formal recommendation for the writing of symbols in the metric system when the basis of the rules as they are now known was laid down.^[101] These rules were subsequently extended by International Organization for Standardization (ISO) and the International Electrotechnical Commission (IEC) and now cover unit symbols and names, prefix symbols and names, how quantity symbols should be written and used and how the values of quantities should be expressed.^{[4]: 104, 130} Both ISO and the IEC have published rules for the presentation of SI units that are generally compatible with those published in the SI Brochure.^[102] As of August 2013^[update] ISO and IEC were in the process of merging their standards for quantities and units into a single set of compatible documents identified as the ISO/IEC 80000 Standard. The rules covering printing of quantities and units are part of ISO 80000-1:2009.^[103]

Names of units follow the grammatical rules associated with common nouns: in English and in French they start with a lowercase letter (e.g., newton, hertz, pascal), even when the symbol for the unit begins with a capital letter. This also applies to "degrees Celsius", since "degree" is the unit.^[104][105] In German, however, the names of units, as with all German nouns, start with capital letters.^[106] The spelling of unit names is a matter for the guardians^{[Note 13]} of the language concerned – the official British and American spellings for certain SI units differ – British English, as well as Australian, Canadian and New Zealand English, uses the spelling deca-, metre, and litre whereas American English uses the spelling deka-, meter, and liter, respectively.^[6]: 3

Likewise, the plural forms of units follow the grammar of the language concerned: in English, the normal rules of English grammar are used, e.g. "henries" is the plural of "henry".^{[107][13]: 31} However, the units lux, hertz, and siemens have irregular plurals in that they remain the same in both their singular and plural form. Plural forms can be even more complicated in other languages. For example, in Polish the plural form depends on the actual quantity: 0 metrów, 1 metr, 2 metry, 3 metry, 4 metry, 5 metrów, 6 metrów, 7 metrów, 8 metrów, etc. For fractions it is metrów, e.g., 0,67 metrów, 2,45 metrów.

In English, when unit names are combined to denote multiplication of the units concerned, they are separated with a hyphen or a space (e.g. newton-metre or newton metre). The plural is formed by converting the last unit name to the plural form (e.g. ten newton-metres).

A space between the number and the unit symbol (i.e., no hyphen) is specified when the combination is used as an adjective, e.g. "a 25 kg sphere".^[4]: 133 However, in English a hyphen would be used as normal in this context if the unit name is spelt out, e.g. "a 25-kilogram sphere".^{[4]: 133 [108]}

Chinese uses traditional logograms for writing the unit names, while in Japanese unit names are written in the phonetic katakana script; in both cases, symbols are also written using the internationally recognised Latin and Greek characters.

Chinese

The basic Chinese units are metre (米 mǐ), litre (升 shēng), gram (克 kè), and second (秒 miǎo), while others include watt (瓦 wǎ). Prefixes include deci- (分 fēn), centi- (厘 lí), milli- (毫 háo), micro- (微 wēi), kilo- (千 qiān), and mega- (兆 zhào). These are combined to form disyllabic characters, such as 厘米 límǐ "centimetre" or 千瓦 qiānwǎ "kilowatt".^[109] In the 19th century, various compound characters were also used, similar to Japanese, either imported or formed on the same principles, such as 瓩 for 千瓦 qiānwǎ (kilowatt) or 糎 for 厘米. These are generally not used today, but are occasionally found in older or technical writing.^[110]

Some units have different names in Taiwan. Metre (公尺), centimetre (公分), litre (公升), kilogram (公斤), gram (公克) and hectare (公頃) have the prefix "公", which means "universal". The prefixes "兆", "分" and "厘" are not commonly used, and the use of "千" is limited to kilowatt (千瓦).

Japanese

A set of characters representing various metric units was created in Japan in the late 19th century. Characters, which are the same in Chinese, exist for three base units: the metre (米), litre (升) and gram (瓦). These were combined with a set of six prefix characters – kilo- (千), hecto- (百), deca- (十), deci- (分), centi- (厘) and milli- (毛) – to form an additional 18 single-character units. The seven length units (kilometre to millimetre), for example, are 粁, 粨, 籵, 米, 粉, 糎 and 粍. These characters, however, are not in common use today; instead, units are written in katakana, the Japanese syllabary used for foreign borrowings, such as キロメートル (kiromētoru) for kilometre, but are also written in standard prefixes such as "km" for kilometre. A few Sino-Japanese words for these units remain in use in Japanese, most significantly "平米" (heibei) for "square metre", but otherwise borrowed pronunciations are used.

These characters are examples of the rare phenomenon of single-character loan words – a foreign word represented by a single Japanese character – and form the plurality of such words. Similar characters were also coined for other units, such as British units, though these also have fallen out of use; see Single character gairaigo: Metric units and Single character gairaigo: Other units for a full list.

Although the writing of unit names is language-specific, the writing of unit symbols and the values of quantities is consistent across all languages and therefore the SI Brochure has specific rules in respect of writing them.^{[4]: 130–135} The guideline produced by the National Institute of Standards and Technology (NIST)^[111] clarifies language-specific areas in respect of American English that were left open by the SI Brochure, but is otherwise identical to the SI Brochure.^[107]

General rules^{[Note 14]} for writing SI units and quantities apply to text that is either handwritten or produced using an automated process:

• The value of a quantity is written as a number followed by a space (representing a multiplication sign) and a unit symbol; e.g., 2.21 kg, 7.3×10² m², 22 K. This rule explicitly includes the percent sign (%)^[4]: 134 and the symbol for degrees of temperature (°C).^[4]: 133 Exceptions are the symbols for plane angular degrees, minutes, and seconds (°, ′, and ″), which are placed immediately after the number with no intervening space.
• Symbols are mathematical entities, not abbreviations, and as such do not have an appended period/full stop (.), unless the rules of grammar demand one for another reason, such as denoting the end of a sentence.
• A prefix is part of the unit, and its symbol is prepended to the unit symbol without a separator (e.g., k in km, M in MPa, G in GHz). Compound prefixes are not allowed.
• Symbols for derived units formed by multiplication are joined with a centre dot (·) or a non-breaking space; e.g., N·m or N m.
• Symbols for derived units formed by division are joined with a solidus (/), or given as a negative exponent. E.g., the "metre per second" can be written m/s, m s⁻¹, m·s⁻¹, or ⁠m/s⁠. Only one solidus should be used; e.g., kg/(m·s²) and kg·m⁻¹·s⁻² are acceptable, but kg/m/s² is ambiguous and unacceptable.

• The first letter of symbols for units derived from the name of a person is written in upper case; otherwise, they are written in lower case. E.g., the unit of pressure is named after Blaise Pascal, so its symbol is written "Pa", but the symbol for mole is written "mol". Thus, "T" is the symbol for tesla, a measure of magnetic field strength, and "t" the symbol for tonne, a measure of mass. Since 1979, the litre may exceptionally be written using either an uppercase "L" or a lowercase "l", a decision prompted by the similarity of the lowercase letter "l" to the numeral "1", especially with certain typefaces or English-style handwriting. The American NIST recommends that within the United States "L" be used rather than "l".
• Symbols of units do not have a plural form; e.g., 25 kg, not 25 kgs.
• Uppercase and lowercase prefixes are not interchangeable. E.g., the quantities 1 mW and 1 MW represent two different quantities; the former is the typical power requirement of a hearing aid (1 milliwatt or 0.001 watts), and the latter the typical power requirement of a suburban train (1 megawatt or 1000000 watts).
• The 10th resolution of CGPM in 2003 declared that "the symbol for the decimal marker shall be either the point on the line or the comma on the line." In practice, the decimal point is used in English-speaking countries and most of Asia, and the comma in most of Latin America and in continental European countries.^[112]
• Spaces should be used as a thousands separator (1000000) in contrast to commas or periods (1,000,000 or 1.000.000) to reduce confusion resulting from the variation between these forms in different countries.
• Any line-break inside a number, inside a compound unit, or between number and unit should be avoided. Where this is not possible, line breaks should coincide with thousands separators.
• Since the value of "billion" and "trillion" can vary from language to language, the dimensionless terms "ppb" (parts per billion) and "ppt" (parts per trillion) should be avoided. No alternative is suggested in the SI Brochure.

Further rules^{[Note 14]} are specified in respect of production of text using printing presses, word processors, typewriters and the like.

• Symbols are written in upright (Roman) type (m for metres, s for seconds), so as to differentiate from the italic type used for quantities (m for mass, s for displacement). By consensus of international standards bodies, this rule is applied independent of the font used for surrounding text.
• In Chinese, Japanese, and Korean language computing (CJK), some of the commonly used units, prefix–unit combinations, or unit–exponent combinations have been allocated predefined single characters taking up a full square. Unicode includes these in its CJK Compatibility^[113] and letter-like symbols^[114] sub-ranges for back compatibility, without necessarily recommending future usage. These are summarised in Unicode symbols. The cursive ℓ, a letter-like symbol, has been used in a number of countries in addition to China and Japan as a symbol for the litre, but this is not currently recommended by any standards body.
• In print, the space used as a thousands separator (commonly called a thin space) is typically narrower than that used between words.

• International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. Electronic version.
• Unit Systems in Electromagnetism
• MW Keller et al. Metrology Triangle Using a Watt Balance, a Calculable Capacitor, and a Single-Electron Tunneling Device
• "The Current SI Seen From the Perspective of the Proposed New SI". Barry N. Taylor. Journal of Research of the National Institute of Standards and Technology, Vol. 116, No. 6, Pgs. 797–807, Nov–Dec 2011.
• B. N. Taylor, Ambler Thompson, International System of Units (SI), National Institute of Standards and Technology 2008 edition, ISBN 1437915582.

Wikimedia Commons has media related to International System of Units.

Official

• BIPM Bureau International des Poids et Mesures (SI maintenance agency) (home page)
  • BIPM brochure (SI reference)
• ISO 80000-1:2009 Quantities and units – Part 1: General
• NIST Official Publications
  • NIST Special Publication 330, 2008 Edition: The International System of Units (SI)
  • NIST Special Publication 811, 2008 Edition: Guide for the Use of the International System of Units
  • NIST Special Pub 814: Interpretation of the SI for the United States and Federal Government Metric Conversion Policy
• Rules for SAE Use of SI (Metric) Units
• International System of Units at Curlie
• EngNet Metric Conversion Chart Online Categorised Metric Conversion Calculator
• U.S. Metric Association. 2008. A Practical Guide to the International System of Units

History

• LaTeX SIunits package manual gives a historical background to the SI system.

Research

• The metrological triangle
• Recommendation of ICWM 1 (CI-2005)