
In 2019, four of the seven SI base units specified in the International System of Quantities were redefined in terms of natural physical constants, rather than human artifacts such as the standard kilogram.[1][2] Effective 20 May 2019, the 144th anniversary of the Metre Convention, the kilogram, ampere, kelvin, and mole are now defined by setting exact numerical values, when expressed in SI units, for the Planck constant (h), the elementary electric charge (e), the Boltzmann constant (kB), and the Avogadro constant (NA), respectively. The second, metre, and candela had previously been redefined using physical constants. The four new definitions aimed to improve the SI without changing the value of any units, ensuring continuity with existing measurements.[3][4] In November 2018, the 26th General Conference on Weights and Measures (CGPM) unanimously approved these changes,[5][6] which the International Committee for Weights and Measures (CIPM) had proposed earlier that year after determining that previously agreed conditions for the change had been met.[7]: 23 These conditions were satisfied by a series of experiments that measured the constants to high accuracy relative to the old SI definitions, and were the culmination of decades of research.
The previous major change of the metric system occurred in 1960 when the International System of Units (SI) was formally published. At this time the metre was redefined: the definition was changed from the prototype of the metre to a certain number of wavelengths of a spectral line of a krypton-86 radiation, making it derivable from universal natural phenomena.[Note 1] The kilogram remained defined by a physical prototype, leaving it the only artifact upon which the SI unit definitions depend. At this time the SI, as a coherent system, was constructed around seven base units, powers of which were used to construct all other units. With the 2019 redefinition, the SI is constructed around seven defining constants, allowing all units to be constructed directly from these constants. The designation of base units is retained but is no longer essential to define the SI units.[4]
The metric system was originally conceived as a system of measurement that was derivable from unchanging phenomena,[8] but practical limitations necessitated the use of artifacts – the prototype of the metre and prototype of the kilogram – when the metric system was introduced in France in 1799. Although they were designed for long-term stability, the prototype kilogram and its secondary copies have shown small variations in mass relative to each other over time; they are not thought to be adequate for the increasing accuracy demanded by science, prompting a search for a suitable replacement. The definitions of some units were defined by measurements that are difficult to precisely realise in a laboratory, such as the kelvin, which was defined in terms of the triple point of water. With the 2019 redefinition, the SI became wholly derivable from natural phenomena with most units being based on fundamental physical constants.
A number of authors have published criticisms of the revised definitions; their criticisms include the premise that the proposal failed to address the impact of breaking the link between the definition of the dalton[Note 2] and the definitions of the kilogram, the mole, and the Avogadro constant.
Background
[edit]The basic structure of the SI was developed over about 170 years between 1791 and 1960. Since 1960, technological advances have made it possible to address weaknesses in the SI such as the dependence on a physical artifact to define the kilogram.
Development of SI
[edit]During the early years of the French Revolution, the leaders of the French National Constituent Assembly decided to introduce a new system of measurement that was based on the principles of logic and natural phenomena. The metre was defined as one ten-millionth of the distance from the north pole to the equator and the kilogram as the mass of one thousandth of a cubic metre of pure water. Although these definitions were chosen to avoid ownership of the units, they could not be measured with sufficient convenience or precision to be of practical use. Instead, realisations were created in the form of the mètre des Archives and kilogramme des Archives which were a "best attempt" at fulfilling these principles.[9]
By 1875, use of the metric system had become widespread in Europe and in Latin America; that year, twenty industrially developed nations met for the Convention of the Metre, which led to the signing of the Treaty of the Metre, under which three bodies were set up to take custody of the international prototypes of the kilogram and the metre, and to regulate comparisons with national prototypes.[10][11] They were:
- CGPM (General Conference on Weights and Measures, Conférence générale des poids et mesures) – The Conference meets every four to six years and consists of delegates of the nations that had signed the convention. It discusses and examines the arrangements required to ensure the propagation and improvement of the International System of Units and it endorses the results of new fundamental metrological determinations.
- CIPM (International Committee for Weights and Measures, Comité international des poids et mesures) – The Committee consists of eighteen eminent scientists, each from a different country, nominated by the CGPM. The CIPM meets annually and is tasked with advising the CGPM. The CIPM has set up a number of sub-committees, each charged with a particular area of interest. One of these, the Consultative Committee for Units (CCU), advises the CIPM on matters concerning units of measurement.[12]
- BIPM (International Bureau for Weights and Measures, Bureau international des poids et mesures) – The Bureau provides safe keeping of the international prototypes of the kilogram and the metre, provides laboratory facilities for regular comparisons of the national prototypes with the international prototype, and is the secretariat for the CIPM and the CGPM.
The 1st CGPM (1889) formally approved the use of 40 prototype metres and 40 prototype kilograms made by the British firm Johnson Matthey as the standards mandated by the Convention of the Metre.[13] The prototypes Metre No. 6 and Kilogram KIII were designated as the international prototype of the metre and the kilogram, respectively; the CGPM retained other copies as working copies, and the rest were distributed to member states for use as their national prototypes. About once every 40 years, the national prototypes were compared with and recalibrated against the international prototype.[14]
In 1921 the Convention of the Metre was revised and the mandate of the CGPM was extended to provide standards for all units of measure, not just mass and length. In the ensuing years, the CGPM took on responsibility for providing standards of electrical current (1946), luminosity (1946), temperature (1948), time (1956), and molar mass (1971).[15] The 9th CGPM in 1948 instructed the CIPM "to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention".[16] The recommendations based on this mandate were presented to the 11th CGPM (1960), where they were formally accepted and given the name "Système International d'Unités" and its abbreviation "SI".[17]
Impetus for change
[edit]There is a precedent for changing the underlying principles behind the definition of the SI base units; the 11th CGPM (1960) defined the SI metre in terms of the wavelength of krypton-86 radiation, replacing the pre-SI metre bar, and the 13th CGPM (1967) replaced the original definition of the second, which was based on Earth's average rotation from 1750 to 1892,[18] with a definition based on the frequency of the radiation emitted or absorbed with a transition between two hyperfine levels of the ground state of the caesium-133 atom. The 17th CGPM (1983) replaced the 1960 definition of the metre with one based on the second by giving an exact definition of the speed of light in units of metres per second.[19]

Since their manufacture, drifts of up to 2×10−8 kilograms (20 μg) per year in the national prototype kilograms relative to the international prototype of the kilogram (IPK) have been detected. There was no way of determining whether the national prototypes were gaining mass or whether the IPK was losing mass.[21] Newcastle University metrologist Peter Cumpson has since identified mercury vapour absorption or carbonaceous contamination as possible causes of this drift.[22][23] At the 21st meeting of the CGPM (1999), national laboratories were urged to investigate ways of breaking the link between the kilogram and a specific artifact.
Metrologists investigated several alternative approaches to redefining the kilogram based on fundamental physical constants. Among others, the Avogadro project and the development of the Kibble balance (known as the "watt balance" before 2016) promised methods of indirectly measuring mass with very high precision. These projects provided tools that enable alternative means of redefining the kilogram.[24]
A report published in 2007 by the Consultative Committee for Thermometry (CCT) to the CIPM noted that their current definition of temperature has proved to be unsatisfactory for temperatures below 20 K and for temperatures above 1300 K. The committee took the view that the Boltzmann constant provided a better basis for temperature measurement than did the triple point of water because it overcame these difficulties.[25]
At its 23rd meeting (2007), the CGPM mandated the CIPM to investigate the use of natural constants as the basis for all units of measure rather than the artifacts that were then in use. The following year this was endorsed by the International Union of Pure and Applied Physics (IUPAP).[26] At a meeting of the CCU held in Reading, United Kingdom, in September 2010, a resolution[27] and draft changes to the SI brochure that were to be presented to the next meeting of the CIPM in October 2010 were agreed to in principle.[28] The CIPM meeting of October 2010 found "the conditions set by the General Conference at its 23rd meeting have not yet been fully met.[Note 4] For this reason the CIPM does not propose a revision of the SI at the present time".[30] The CIPM, however, presented a resolution for consideration at the 24th CGPM (17–21 October 2011) to agree to the new definitions in principle, but not to implement them until the details had been finalised.[31] This resolution was accepted by the conference,[32] and in addition the CGPM moved the date of the 25th meeting forward from 2015 to 2014.[33][34] At the 25th meeting on 18 to 20 November 2014, it was found that "despite [progress in the necessary requirements] the data do not yet appear to be sufficiently robust for the CGPM to adopt the revised SI at its 25th meeting",[35] thus postponing the revision to the next meeting in 2018. Measurements accurate enough to meet the conditions were available in 2017 and the redefinition[36] was adopted at the 26th CGPM (13–16 November 2018).
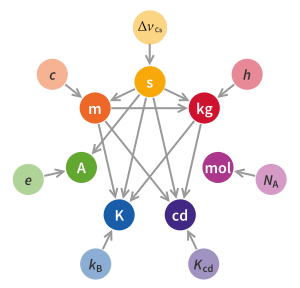
Defining constants
[edit]Following the successful 1983 redefinition of the metre in terms of an exact numerical value for the speed of light, the BIPM's Consultative Committee for Units (CCU) recommended and the BIPM proposed that four further constants of nature should be defined to have exact values. These are:[Note 5]
- The Planck constant h is exactly 6.62607015×10−34 joule-second (J⋅s).
- The elementary charge e is exactly 1.602176634×10−19 coulomb (C).
- The Boltzmann constant k is exactly 1.380649×10−23 joule per kelvin (J⋅K−1).
- The Avogadro constant NA is exactly 6.02214076×1023 reciprocal mole (mol−1).
The redefinition retains unchanged the numerical values associated with the following constants of nature:
- The speed of light c is exactly 299792458 metres per second (m⋅s−1);
- The ground state hyperfine structure transition frequency of the caesium-133 atom ΔνCs is exactly 9192631770 hertz (Hz);
- The luminous efficacy of monochromatic radiation of frequency 5.40×1014 Hz (540 THz) – a frequency of green-colored light at approximately the peak sensitivity of the human eye – Kcd (where the subscript "cd" is the symbol for candela) is exactly 683 lumens per watt (lm⋅W−1).
The seven SI defining constants above, expressed in terms of derived units (joule, coulomb, hertz, lumen, and watt), are rewritten below in terms of the seven base units (second, metre, kilogram, ampere, kelvin, mole, and candela);[4] the dimensionless unit steradian (symbol sr) is also used:
- ΔνCs = Δν(133Cs)hfs = 9192631770 s−1
- c = 299792458 m⋅s−1
- h = 6.62607015×10−34 kg⋅m2⋅s−1
- e = 1.602176634×10−19 A⋅s
- k = 1.380649×10−23 kg⋅m2⋅K−1⋅s−2
- NA = 6.02214076×1023 mol−1
- Kcd = 683 cd⋅sr⋅s3⋅kg−1⋅m−2
As part of the redefinition, the International Prototype of the Kilogram was retired and definitions of the kilogram, the ampere, and the kelvin were replaced. The definition of the mole was revised. These changes have the effect of redefining the SI base units, though the definitions of the SI derived units in terms of the base units remain the same.
Impact on base unit definitions
[edit]Following the CCU proposal, the texts of the definitions of all of the base units were either refined or rewritten, changing the emphasis from explicit-unit- to explicit-constant-type definitions.[38] Explicit-unit-type definitions define a unit in terms of a specific example of that unit; for example, in 1324 Edward II defined the inch as being the length of three barleycorns,[39] and from 1889 to 2019 the kilogram was defined as the mass of the International Prototype of the Kilogram. In explicit-constant definitions, a constant of nature is given a specified value, and the definition of the unit emerges as a consequence; for example, in 2019, the speed of light was defined as exactly 299792458 metres per second. The length of the metre could be derived because the second had been already independently defined. The previous[19] and 2019[4][37] definitions are given below.
Second
[edit]The new definition of the second is effectively the same as the previous one, the only difference being that the conditions under which the definition applies are more rigorously defined.
- Previous definition: The second is the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom.
- 2019 definition: The second, symbol s, is the SI unit of time. It is defined by taking the fixed numerical value of the caesium frequency, ΔνCs, the unperturbed ground-state hyperfine transition frequency of the caesium-133 atom,[Note 6] to be 9192631770 when expressed in the unit Hz, which is equal to s−1.
The second may be expressed directly in terms of the defining constants:
- 1 s = 9192631770/ΔνCs.
Metre
[edit]The new definition of the metre is effectively the same as the previous one, the only difference being that the additional rigour in the definition of the second propagated to the metre.
- Previous definition: The metre is the length of the path travelled by light in vacuum during a time interval of 1/299792458 of a second.
- 2019 definition: The metre, symbol m, is the SI unit of length. It is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299792458 when expressed in the unit m⋅s−1, where the second is defined in terms of the caesium frequency ΔνCs.
The metre may be expressed directly in terms of the defining constants:
- 1 m = 9192631770/299792458c/ΔνCs.
Kilogram
[edit]
The definition of the kilogram fundamentally changed from an artifact (the International Prototype of the Kilogram) to a constant of nature.[41] Because the Planck constant relates photon energy to photon frequency, the new definition relates the kilogram to the mass equivalent of the energy of a photon at a specific frequency.
- Previous definition: The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram.
- 2019 definition: The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of c and ΔνCs.
For illustration, an earlier proposed redefinition that is equivalent to this 2019 definition is: "The kilogram is the mass of a body at rest whose equivalent energy equals the energy of a collection of photons whose frequencies sum to [1.356392489652×1050] hertz."[42]
The kilogram may be expressed directly in terms of the defining constants:
- 1 kg = (299792458)2/(6.62607015×10−34)(9192631770)hΔνCs/c2.
Leading to
- 1 J⋅s = h/6.62607015×10−34
- 1 J = hΔνCs/(6.62607015×10−34)(9192631770)
- 1 W = h(ΔνCs)2/(6.62607015×10−34)(9192631770)2
- 1 N = 299792458/(6.62607015×10−34)(9192631770)2h(ΔνCs)2/c
Ampere
[edit]The definition of the ampere underwent a major revision. The previous definition relied on infinite lengths that are impossible to realise:[43]
- Previous definition: The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 m apart in vacuum, would produce between these conductors a force equal to 2×10−7 newton per metre of length.
The alternative avoided that issue:
- 2019 definition: The ampere, symbol A, is the SI unit of electric current. It is defined by taking the fixed numerical value of the elementary charge e to be 1.602176634×10−19 when expressed in the unit C, which is equal to A⋅s, where the second is defined in terms of ΔνCs.
The ampere may be expressed directly in terms of the defining constants as:
- 1 A = eΔνCs/(1.602176634×10−19)(9192631770)
For illustration, this is equivalent to defining one coulomb to be an exact specified multiple of the elementary charge.
- 1 C = e/1.602176634×10−19
Because the previous definition contains a reference to force, which has the dimensions MLT−2, it follows that in the previous SI the kilogram, metre, and second – the base units representing these dimensions – had to be defined before the ampere could be defined. Other consequences of the previous definition were that in SI the value of vacuum permeability (μ0) was fixed at exactly 4π×10−7 H⋅m-1.[44]
A consequence of the revised definition is that the ampere no longer depends on the definitions of the kilogram and the metre; it does, however, still depend on the definition of the second. In addition, the numerical values when expressed in SI units of the vacuum permeability, vacuum permittivity, and impedance of free space, which were exact before the redefinition, are subject to experimental error after the redefinition.[45] For example, the numerical value of the vacuum permeability has a relative uncertainty equal to that of the experimental value of the fine-structure constant .[46] The CODATA 2018 value for the relative standard uncertainty of is 1.6×10−10.[47] [Note 7]
The ampere definition leads to exact values for
- 1 V = 1.602176634×10−19/(6.62607015×10−34)(9192631770)hΔνCs/e
- 1 Wb = 1.602176634×10−19/6.62607015×10−34h/e
- 1 Ω = (1.602176634×10−19)2/6.62607015×10−34h/e2
Kelvin
[edit]The definition of the kelvin underwent a fundamental change. Rather than using the triple point of water to fix the temperature scale, the new definition uses the energy equivalent as given by Boltzmann's equation.
- Previous definition: The kelvin, unit of thermodynamic temperature, is 1/273.16 of the thermodynamic temperature of the triple point of water.
- 2019 definition: The kelvin, symbol K, is the SI unit of thermodynamic temperature. It is defined by taking the fixed numerical value of the Boltzmann constant k to be 1.380649×10−23 when expressed in the unit J⋅K−1, which is equal to kg⋅m2⋅s−2⋅K−1, where the kilogram, metre and second are defined in terms of h, c and ΔνCs.
The kelvin may be expressed directly in terms of the defining constants as:
- 1 K = 1.380649×10−23/(6.62607015×10−34)(9192631770)hΔνCs/k.
Mole
[edit]
The previous definition of the mole linked it to the kilogram. The revised definition breaks that link by making a mole a specific number of entities of the substance in question.
- Previous definition: The mole is the amount of substance of a system that contains as many elementary entities as there are atoms in 0.012 kilogram of carbon-12. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
- 2019 definition:[7]: 22 The mole, symbol mol, is the SI unit of amount of substance. One mole contains exactly 6.02214076×1023 elementary entities. This number is the fixed numerical value of the Avogadro constant, NA, when expressed in the unit mol−1 and is called the Avogadro number.[7][48] The amount of substance, symbol n, of a system is a measure of the number of specified elementary entities. An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles.
The mole may be expressed directly in terms of the defining constants as:
- 1 mol = 6.02214076×1023/NA.
One consequence of this change is that the previously defined relationship between the mass of the 12C atom, the dalton, the kilogram, and the Avogadro constant is no longer valid. One of the following had to change:
- The mass of a 12C atom, unbound and in its electronic and nuclear ground states, is exactly 12 dalton.
- The number of dalton in a gram is exactly the numerical value of the Avogadro constant: (i.e., 1 g/Da = 1 mol ⋅ NA).
The wording of the 9th SI Brochure[4][Note 8] implies that the first statement remains valid, which means the second is no longer true. The molar mass constant, while still with great accuracy remaining 1 g/mol, is no longer exactly equal to that. Appendix 2 to the 9th SI Brochure states that "the molar mass of carbon 12, M(12C), is equal to 0.012 kg⋅mol−1 within a relative standard uncertainty equal to that of the recommended value of NAh at the time this Resolution was adopted, namely 4.5×10−10, and that in the future its value will be determined experimentally",[49][50] which makes no reference to the dalton and is consistent with either statement.
Candela
[edit]The new definition of the candela is effectively the same as the previous definition as dependent on other base units, with the result that the redefinition of the kilogram and the additional rigour in the definitions of the second and metre propagate to the candela.
- Previous definition: The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×1012 Hz and that has a radiant intensity in that direction of 1/683 watt per steradian.
- 2019 definition: The candela, symbol cd, is the SI unit of luminous intensity in a given direction. It is defined by taking the fixed numerical value of the luminous efficacy of monochromatic radiation of frequency 540×1012 Hz, Kcd, to be 683 when expressed in the unit lm⋅W−1, which is equal to cd⋅sr⋅W−1, or cd⋅sr⋅kg−1⋅m−2⋅s3, where the kilogram, metre and second are defined in terms of h, c and ΔνCs.
- 1 cd = 1/683(6.62607015×10−34)(9192631770)2Kcdh(ΔνCs)2
Impact on reproducibility
[edit]All seven of the SI base units are defined in terms of defined constants[Note 9] and universal physical constants.[Note 10][51] Seven constants are needed to define the seven base units but there is not a direct correspondence between each specific base unit and a specific constant; except the second and the mole, more than one of the seven constants contributes to the definition of any given base unit.
When the New SI was first designed, there were more than six suitable physical constants from which the designers could choose. For example, once length and time had been established, the universal gravitational constant G could, from a dimensional point of view, be used to define mass.[Note 11] In practice, G can only be measured with a relative uncertainty of the order of 10−5,[Note 12] which would have resulted in the upper limit of the kilogram's reproducibility being around 10−5 whereas the then-current international prototype of the kilogram can be measured with a reproducibility of 1.2 × 10−8.[45] The physical constants were chosen on the basis of minimal uncertainty associated with measuring the constant and the degree of independence of the constant in respect of other constants that were being used. Although the BIPM has developed a standard mise en pratique (practical technique)[52] for each type of measurement, the mise en pratique used to make the measurement is not part of the measurement's definition – it is merely an assurance that the measurement can be done without exceeding the specified maximum uncertainty.
Acceptance
[edit]Much of the work done by the CIPM is delegated to consultative committees. The CIPM Consultative Committee for Units (CCU) has made the proposed changes while other committees have examined the proposal in detail and have made recommendations regarding their acceptance by the CGPM in 2014. The consultative committees have laid down a number of criteria that must be met before they will support the CCU's proposal, including:
- For the redefinition of the kilogram, at least three separate experiments yielding values for the Planck constant having a relative expanded (95%) uncertainty of no more than 5×10−8 must be carried out and at least one of these values should be better than 2×10−8. Both the Kibble balance and the Avogadro project should be included in the experiments and any differences between these must be reconciled.[53][54]
- For the redefinition of the kelvin, the relative uncertainty of the Boltzmann constant derived from two fundamentally different methods such as acoustic gas thermometry and dielectric constant gas thermometry must be better than 10−6, and these values must be corroborated by other measurements.[55]
As of March 2011, the International Avogadro Coordination (IAC) group had obtained an uncertainty of 3.0×10−8 and NIST had obtained an uncertainty of 3.6×10−8 in their measurements.[24] On 1 September 2012 the European Association of National Metrology Institutes (EURAMET) launched a formal project to reduce the relative difference between the Kibble balance and the silicon sphere approach to measuring the kilogram from (17±5)×10−8 to within 2×10−8.[56] As of March 2013[update] the proposed redefinition is known as the "New SI"[3] but Mohr, in a paper following the CGPM proposal but predating the formal CCU proposal, suggested that because the proposed system makes use of atomic scale phenomena rather than macroscopic phenomena, it should be called the "Quantum SI System".[57]
As of the 2014 CODATA-recommended values of the fundamental physical constants published in 2016 using data collected until the end of 2014, all measurements met the CGPM's requirements, and the redefinition and the next CGPM quadrennial meeting in late 2018 could now proceed.[58][59]
On 20 October 2017, the 106th meeting of the International Committee for Weights and Measures (CIPM) formally accepted a revised Draft Resolution A, calling for the redefinition of the SI, to be voted on at the 26th CGPM,[7]: 17–23 The same day, in response to the CIPM's endorsement of the final values,[7]: 22 the CODATA Task Group on Fundamental Constants published its 2017 recommended values for the four constants with uncertainties and proposed numerical values for the redefinition without uncertainty.[37] The vote, which was held on 16 November 2018 at the 26th GCPM, was unanimous; all attending national representatives voted in favour of the revised proposal.
The new definitions became effective on 20 May 2019.[60]
Concerns
[edit]In 2010, Marcus Foster of the Australian Commonwealth Scientific and Industrial Research Organisation (CSIRO) published a wide-ranging critique of the SI; he raised numerous issues ranging from basic issues such as the absence of the symbol "Ω" (omega, used for the ohm) from most Western computer keyboards to abstract issues such as inadequate formalism in the metrological concepts on which SI is based. The changes proposed in the new SI only addressed problems with the definition of the base units, including new definitions of the candela and the mole – units Foster argued are not true base units. Other issues raised by Foster fell outside the scope of the proposal.[61]
Explicit-unit and explicit-constant definitions
[edit]Concerns have been expressed that the use of explicit-constant definitions of the unit being defined that are not related to an example of its quantity will have many adverse effects.[62] Although this criticism applies to the linking of the kilogram to the Planck constant h via a route that requires a knowledge of both special relativity and quantum mechanics,[63] it does not apply to the definition of the ampere, which is closer to an example of its quantity than is the previous definition.[64] Some observers have welcomed the change to base the definition of electric current on the charge of the electron rather than the previous definition of a force between two parallel, current-carrying wires; because the nature of the electromagnetic interaction between two bodies is somewhat different at the quantum electrodynamics level than at classical electrodynamic levels, it is considered inappropriate to use classical electrodynamics to define quantities that exist at quantum electrodynamic levels.[45]
Mass and the Avogadro constant
[edit]When the scale of the divergence between the IPK and national kilogram prototypes was reported in 2005, a debate began about whether the kilogram should be defined in terms of the mass of the silicon-28 atom or by using the Kibble balance. The mass of a silicon atom could be determined using the Avogadro project and using the Avogadro constant, it could be linked directly to the kilogram.[65] Concerns that the authors of the proposal had failed to address the impact of breaking the link between the mole, kilogram, dalton, and the Avogadro constant (NA) have also been expressed.[Note 13] This direct link has caused many to argue that the mole is not a true physical unit but, according to the Swedish philosopher Johansson, a "scaling factor".[61][66]
The 8th edition of the SI Brochure defined the dalton in terms of the mass of an atom of 12C.[67] It defined the Avogadro constant in terms of this mass and the kilogram, making it determined by experiment. The redefinition fixes the Avogadro constant and the 9th SI Brochure[4] retains the definition of dalton in terms of 12C, with the effect that the link between the dalton and the kilogram will be broken.[68][69]
In 1993, the International Union of Pure and Applied Chemistry (IUPAC) approved the use of the dalton as an alternative to the unified atomic mass unit with the qualification that the CGPM had not given its approval.[70] This approval has since been given.[71] Following the proposal to redefine the mole by fixing the value of the Avogadro constant, Brian Leonard of the University of Akron, writing in Metrologia, proposed that the dalton (Da) be redefined such that NA = (g/Da) mol−1, but that the unified atomic mass unit (mu) retain its current definition based on the mass of 12C, ceasing to exactly equal the dalton. This would result in the dalton and the atomic mass unit potentially differing from each other with a relative uncertainty of the order of 10−10.[72] The 9th SI Brochure, however, defines both the dalton (Da) and the unified atomic mass unit (u) as exactly 1/12 of the mass of a free carbon-12 atom and not in relation to the kilogram,[4] with the effect that the above equation will be inexact.
Temperature
[edit]Different temperature ranges need different measurement methods. Room temperature can be measured by means of expansion and contraction of a liquid in a thermometer but high temperatures are often associated with colour of blackbody radiation. Wojciech T. Chyla, approaching the structure of SI from a philosophical point of view in the Journal of the Polish Physical Society, argued that temperature is not a real base unit but is an average of the thermal energies of the individual particles that comprise the body concerned.[45] He noted that in many theoretical papers, temperature is represented by the quantities Θ or β where
and k is the Boltzmann constant. Chyla acknowledged, however, that in the macroscopic world, temperature plays the role of a base unit because much of the theory of thermodynamics is based on temperature.[45]
The Consultative Committee for Thermometry, part of the International Committee for Weights and Measures, publishes a mise en pratique (practical technique), last updated in 1990, for measuring temperature. At very low and at very high temperatures it often links energy to temperature via the Boltzmann constant.[73][74]
Luminous intensity
[edit]Foster argued that "luminous intensity [the candela] is not a physical quantity, but a photobiological quantity that exists in human perception", questioning whether the candela should be a base unit.[61] Before the 1979 decision to define photometric units in terms of luminous flux (power) rather than luminous intensities of standard light sources, there was already doubt whether there should still be a separate base unit for photometry. Furthermore, there was unanimous agreement that the lumen was now more fundamental than the candela. However, for the sake of continuity the candela was kept as base unit.[75]
See also
[edit]- International System of Units – Modern form of the metric system
- International Vocabulary of Metrology – Committee under the chairmanship of the director of the BIPM
- Physical constant – Universal and unchanging physical quantity
- SI base unit – One of the seven units of measurement that define the metric system
- 2005–2019 definitions of the SI base units
- Non-SI units mentioned in the SI – Unit accepted for use in the International System of Units – changes associated with the 2019 redefinition
Notes
[edit]- ^ The metre was redefined again in 1983 by fixing the value of the speed of light in vacuum. That definition went unaltered in 2019 and remains in effect today.
- ^ The dalton is not defined in the formal proposal to be voted upon by the CGPM, only in the 9th edition of the SI Brochure.
- ^ Prototype No. 8(41) was accidentally stamped with the number 41, but its accessories carry the proper number 8. Since there is no prototype marked 8, this prototype is referred to as 8(41).
- ^ In particular the CIPM was to prepare a detailed mise en pratique for each of the new definitions of the kilogram, ampere, kelvin and mole set by the 23rd CGPM.[29]
- ^ These constants are described in the 2006 version of the SI manual but in that version, the latter three are defined as "constants to be obtained by experiment" rather than as "defining constants".
- ^ Although the phrase used here is more terse than in the previous definition, it still has the same meaning. This is made clear in the 9th SI Brochure, which almost immediately after the definition on p. 130 states: "The effect of this definition is that the second is equal to the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the unperturbed ground state of the 133Cs atom."
- ^ A note should be added on the definition of magnetic field unit (tesla). When the ampere was defined as the current that when flows in two long parallel wires separated by 1 m causes a force of 2×10−7 N/m on each other, there was also another definition: the magnetic field at the location of each of the wires in this configuration was defined to be 2×10−7 T. Namely 1 T is the intensity of the magnetic field B that causes a force of 1 N/m on a wire carrying a current of 1 A. The number 2×10−7 was written also as μ0/2π. This arbitrary definition is what made μ0 to be exactly 4π×10−7 H/m. Accordingly, the magnetic field near a wire carrying current is given by B = μ0I/2πr. Now, with the new definition of the ampere, the definition of the tesla is also affected. More specifically, the definition relying on the force of a magnetic field on a wire carrying current is maintained (F = I⋅B⋅l) while, as mentioned above, μ0 can no longer be exactly 4π×10−7 H/m and has to be measured experimentally. The value of the vacuum permittivity ε0 = 1/(μ0c2) is also affected accordingly. The Maxwell equations will 'see to it' that the electrostatic force between two point charges will be F = 1/(4πε0)(q1q2)/r2.
- ^ A footnote in Table 8 on non-SI units states: "The dalton (Da) and the unified atomic mass unit (u) are alternative names (and symbols) for the same unit, equal to 1/12 of the mass of a free carbon 12 atom, at rest and in its ground state."
- ^ Though the three quantities temperature, luminous intensity and amount of substance may be regarded from a fundamental physical perspective as derived quantities, these are perceptually independent quantities and have conversion constants defined that relate the historically defined units to the underlying physics.
- ^ The definition of the candela is atypical within the base units; translating physical measurements of spectral intensity into units of candela also requires a model of the response of the human eye to different wavelengths of light known as the luminosity function and denoted by V(λ), a function that is determined by the International Commission on Illumination (CIE).
- ^ The dimensions of G are L3M−1T−2 so once standards have been established for length and for time, mass can, in theory, be deduced from G. When fundamental constants as relations between these three units are set, the units can be deduced from a combination of these constants; for example, as a linear combination of Planck units.
- ^
The following terms are defined in International vocabulary of metrology – Basic and general concepts and associated terms Archived 17 March 2017 at the Wayback Machine:
- measurement reproducibility – definition 2.25
- standard measurement uncertainty – definition 2.30
- relative standard measurement uncertainty – definition 2.32
- ^ The two quantities of the Avogadro constant NA and the Avogadro number NN are numerically identical but while NA has the unit mol−1, NN is a pure number.
References
[edit]- ^ "BIPM statement: Information for users about the proposed revision of the SI" (PDF). Archived (PDF) from the original on 21 January 2018. Retrieved 5 May 2018.
- ^ "Decision CIPM/105-13 (October 2016)". Archived from the original on 24 August 2017. Retrieved 31 August 2017.
- ^ a b Kühne, Michael (22 March 2012). "Redefinition of the SI". Keynote address, ITS9 (Ninth International Temperature Symposium). Los Angeles: NIST. Archived from the original on 18 June 2013. Retrieved 1 March 2012.
- ^ a b c d e f g "9th edition of the SI Brochure". BIPM. 2019. Retrieved 20 May 2019.
- ^ "Historic Vote Ties Kilogram and Other Units to Natural Constants". NIST. 16 November 2018. Archived from the original on 18 November 2018. Retrieved 16 November 2018.
- ^ Milton, Martin (14 November 2016). Highlights in the work of the BIPM in 2016 (PDF). SIM XXII General Assembly. Montevideo, Uruguay. p. 10. Archived from the original (PDF) on 1 September 2017. Retrieved 13 January 2017. The conference ran from 13–16 November and the vote on the redefinition was scheduled for the last day. Kazakhstan was absent and did not vote.
- ^ a b c d e Proceedings of the 106th meeting (PDF). International Committee for Weights and Measures. Sèvres. 16–20 October 2017. Archived (PDF) from the original on 27 January 2018. Retrieved 27 January 2018.
- ^ Crease, Robert P. (2011). "France: "Realities of Life and Labor"". World in the Balance. New York: W. W. Norton & Company, Inc. pp. 83–84. ISBN 978-0-393-07298-3.
- ^ Alder, Ken (2002). The Measure of all Things – The Seven-Year-Odyssey that Transformed the World. London: Abacus. p. 1. ISBN 978-0-349-11507-8.
- ^ "Metric Convention of 1875 [English translation]". Washington, D.C.: Office of the President of the United States. 1876. Archived from the original on 1 March 2005.
((cite journal)): Cite journal requires|journal=(help) - ^ "The Metre Convention". Sèvres, France: International Bureau of Weights and Measures. Archived from the original on 26 September 2012. Retrieved 21 June 2013.
- ^ "CIPM: International Committee for Weights and Measures". Sèvres, France: BIPM. Archived from the original on 24 September 2012. Retrieved 3 October 2010.
- ^ "Resolution of the 1st meeting of the CGPM (1889)". Sèvres, France: International Bureau of Weights and Measures. Archived from the original on 21 May 2013. Retrieved 21 June 2013.
- ^ Jabbour, Z.J.; Yaniv, S.L. (2001). "The Kilogram and Measurements of Mass and Force" (PDF). Journal of Research of the National Institute of Standards and Technology. 106 (1): 25–46. doi:10.6028/jres.106.003. PMC 4865288. PMID 27500016. Archived from the original (PDF) on 4 June 2011. Retrieved 28 March 2011.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 95, 97, 138–140, ISBN 92-822-2213-6, archived (PDF) from the original on 4 June 2021, retrieved 16 December 2021
- ^ "Resolution 6 of the 9th meeting of the CGPM (1948): Proposal for establishing a practical system of units of measurement". Archived from the original on 14 May 2013. Retrieved 23 March 2011.
- ^ "Resolution 12 of the 11th meeting of the CGPM (1960): Système International d'Unités". Sèvres, France. Archived from the original on 14 May 2013. Retrieved 23 March 2011.
- ^ Stephenson, F. R.; Morrison, L. V.; Hohenkerk, C. Y. (December 2016). "Measurement of the Earth's rotation: 720 BC to AD 2015". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 472 (2196). §4(a). Bibcode:2016RSPSA.47260404S. doi:10.1098/rspa.2016.0404. PMC 5247521. PMID 28119545.
- ^ a b International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 112–116, ISBN 92-822-2213-6, archived (PDF) from the original on 4 June 2021, retrieved 16 December 2021
- ^ Girard, G. (1994). "The Third Periodic Verification of National Prototypes of the Kilogram (1988–1992)". Metrologia. 31 (4): 317–336. Bibcode:1994Metro..31..317G. doi:10.1088/0026-1394/31/4/007. S2CID 250743540.
- ^ Peter, Mohr (6 December 2010). "Recent progress in fundamental constants and the International System of Units" (PDF). Third Workshop on Precision Physics and Fundamental Physical Constant. Archived from the original (PDF) on 24 August 2011. Retrieved 2 January 2011.
- ^ Whipple, Tom (7 January 2013). "The dirty secret of why you are not quite as heavy as you think". The Times. London. p. 15. Archived from the original on 17 January 2013. Retrieved 23 March 2011.
- ^ Ghose, Tia (6 January 2013). "The Kilogram Has Gained Weight". LiveScience. Archived from the original on 26 March 2013. Retrieved 23 March 2011.
- ^ a b Crease, Robert P. (22 March 2011). "Metrology in the balance". Physics World. 24 (3): 39–45. Bibcode:2011PhyW...24c..39C. doi:10.1088/2058-7058/24/03/34. Retrieved 28 June 2012.
- ^ Fischer, J.; et al. (2 May 2007). "Report to the CIPM on the implications of changing the definition of the base unit kelvin" (PDF). Archived (PDF) from the original on 23 November 2008. Retrieved 2 January 2011.
- ^ "Resolution proposal submitted to the IUPAP Assembly by Commission C2 (SUNAMCO)" (PDF). International Union of Pure and Applied Physics. 2008. Archived (PDF) from the original on 5 March 2016. Retrieved 6 September 2015.
- ^ Mills, Ian (29 September 2010). "On the possible future revision of the International System of Units, the SI" (PDF). CCU. Archived (PDF) from the original on 13 January 2012. Retrieved 1 January 2011.
- ^ Mills, Ian (29 September 2010). "Draft Chapter 2 for SI Brochure, following redefinitions of the base units" (PDF). CCU. Archived (PDF) from the original on 16 March 2012. Retrieved 1 January 2011.
- ^ "Resolution 12 of the 23rd meeting of the CGPM (2007)". Sèvres, France: General Conference on Weights and Measures. Archived from the original on 21 April 2013. Retrieved 21 June 2013.
- ^ "Towards the "new SI"". International Bureau of Weights and Measures (BIPM). Archived from the original on 14 May 2011. Retrieved 20 February 2011.
- ^ "On the possible future revision of the International System of Units, the SI – Draft Resolution A" (PDF). International Committee for Weights and Measures (CIPM). Archived (PDF) from the original on 6 August 2011. Retrieved 14 July 2011.
- ^ "Resolution 1: On the possible future revision of the International System of Units, the SI" (PDF). 24th meeting of the General Conference on Weights and Measures. Sèvres, France: International Bureau for Weights and Measures. 21 October 2011. It was not expected to be adopted until some prerequisite conditions are met, and in any case not before 2014. See"Possible changes to the international system of units". IUPAC Wire. 34 (1). January–February 2012.
- ^ "General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram" (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. 23 October 2011. Archived (PDF) from the original on 9 February 2012. Retrieved 25 October 2011.
- ^ Mohr, Peter (2 November 2011). "Redefining the SI base units". NIST Newsletter. NIST. Archived from the original on 12 August 2016. Retrieved 1 March 2012.
- ^ "Resolutions adopted by the CGPM at its 25th meeting (18–20 November 2014)" (PDF). Sèvres, France: International Bureau for Weights and Measures. 21 November 2014. Archived (PDF) from the original on 25 March 2015. Retrieved 1 December 2014.
- ^ a b "Draft Resolution A "On the revision of the International System of units (SI)" to be submitted to the CGPM at its 26th meeting (2018)" (PDF). Archived (PDF) from the original on 29 April 2018. Retrieved 5 May 2018.
- ^ a b c Newell, David B.; Cabiati, F.; Fischer, J.; Fujii, K.; Karshenboim, S.G.; Margolis, H.S.; de Mirandés, E.; Mohr, P.J.; Nez, F.; Pachucki, K.; Quinn, T.J.; Taylor, B.N.; Wang, M.; Wood, B.M.; Zhang, Z.; et al. (CODATA Task Group on Fundamental Constants) (20 October 2017). "The CODATA 2017 Values of h, e, k, and NA for the Revision of the SI". Metrologia. 55 (1): L13. Bibcode:2018Metro..55L..13N. doi:10.1088/1681-7575/aa950a.
- ^ Mills, Ian (September–October 2011). "Part II – Explicit-Constant Definitions for the Kilogram and for the Mole". Chemistry International. 33 (5): 12–15. ISSN 0193-6484. Archived from the original on 9 July 2017. Retrieved 28 June 2013.
- ^ Travenor, Robert (2007). Smoot's Ear – The Measure of Humanity. Yale University Press. pp. 35–36. ISBN 978-0-300-14334-8.
- ^ a b "The BIPM watt balance". International Bureau of Weights and Measures. 2012. Archived from the original on 21 April 2013. Retrieved 28 March 2013.
- ^ Taylor, Barry N (November–December 2011). "The Current SI Seen From the Perspective of the Proposed New SI". Journal of Research of the National Institute of Standards and Technology. 116 (6): 797–80. doi:10.6028/jres.116.022. PMC 4551220. PMID 26989600.
- ^ Taylor, Barry N; Mohr, Peter J (November 1999). "On the redefinition of the kilogram". Metrologia. 36 (1): 63–64. Bibcode:1999Metro..36...63T. doi:10.1088/0026-1394/36/1/11. S2CID 250823638.
- ^ "Ampere: Introduction". NIST. 15 May 2018. Retrieved 30 May 2024.
- ^ "Unit of electric current (ampere)". Historical context of the SI. NIST. Archived from the original on 3 June 2013. Retrieved 7 September 2015.
- ^ a b c d e Chyla, W.T. (December 2011). "Evolution of the International Metric System of Units SI". Acta Physica Polonica A. 120 (6): 998–1011. Bibcode:2011AcPPA.120..998C. doi:10.12693/APhysPolA.120.998.
- ^ Davis, Richard S. (2017). "Determining the value of the fine-structure constant from a current balance: getting acquainted with some upcoming changes to the SI". American Journal of Physics. 85 (5): 364–368. arXiv:1610.02910. Bibcode:2017AmJPh..85..364D. doi:10.1119/1.4976701. S2CID 119283799.
- ^ "2022 CODATA Value: fine-structure constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 18 May 2024.
- ^ "Redefining the Mole". NIST. 23 October 2018. Archived from the original on 24 October 2018. Retrieved 24 October 2018.
- ^ "Resolutions adopted" (PDF). Bureau international des poids et mesures. November 2018. Archived from the original (PDF) on 4 February 2020. Retrieved 4 February 2020.
- ^ Nawrocki, Waldemar (30 May 2019). Introduction to Quantum Metrology: The Revised SI System and Quantum Standards. Springer. p. 54. ISBN 978-3-030-19677-6.
- ^ Wyszecki, G.; Blevin, W.R.; Kessler, K.G.; Mielenz, K.D. (1983). Principles covering Photometry (PDF). Sevres: Conférence général des poids et mesures (CGPM). Archived (PDF) from the original on 11 October 2008. Retrieved 23 April 2012.
- ^
"What is a mise en pratique?". BIPM. 2011. Archived from the original on 22 September 2015. Retrieved 6 September 2015.
is a set of instructions that allows the definition to be realised in practice at the highest level.
- ^ "Recommendations of the Consultative Committee for Mass and Related Quantities to the International Committee for Weights and Measures" (PDF). 12th Meeting of the CCM. Sèvres: Bureau International des Poids et Mesures. 26 March 2010. Archived from the original (PDF) on 14 May 2013. Retrieved 27 June 2012.
- ^ "Recommendations of the Consultative Committee for Amount of Substance: Metrology in Chemistry to the International Committee for Weights and Measures" (PDF). 16th Meeting of the CCQM. Sèvres: Bureau International des Poids et Mesures. 15–16 April 2010. Archived from the original (PDF) on 14 May 2013. Retrieved 27 June 2012.
- ^ "Recommendations of the Consultative Committee for Thermometry to the International Committee for Weights and Measures" (PDF). 25th Meeting of the Consultative Committee for Thermometry. Sèvres: Bureau International des Poids et Mesures. 6–7 May 2010. Archived from the original (PDF) on 14 May 2013. Retrieved 27 June 2012.
- ^ "kilogram NOW – Realization of the awaited definition of the kilogram". European Association of National Metrology Institutes. Archived from the original on 4 March 2016. Retrieved 8 October 2012.
- ^
Mohr, Peter J. (2008). The Quantum SI: A Possible New International System of Units. Vol. 53. Academic Press. p. 34. Bibcode:2008AdQC...53...27M. doi:10.1016/s0065-3276(07)53003-0. ISBN 978-0-12-373925-4. Retrieved 2 April 2012.
((cite book)):|journal=ignored (help) - ^ "Universe's Constants Now Known with Sufficient Certainty to Completely Redefine the International System of Units" (Press release). NIST. 22 November 2016. Archived from the original on 1 January 2017. Retrieved 31 December 2016.
- ^ Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (26 September 2016). "CODATA recommended values of the fundamental physical constants: 2014". Reviews of Modern Physics. 88 (3): 035009–1–73. arXiv:1507.07956. Bibcode:2016RvMP...88c5009M. doi:10.1103/RevModPhys.88.035009. S2CID 1115862.
This is a truly major development, because these uncertainties are now sufficiently small that the adoption of the new SI by the 26th CGPM is expected.
- ^ Conover, Emily (16 November 2018). "It's official: We're redefining the kilogram". Science News. Archived from the original on 16 November 2018. Retrieved 16 November 2018.
- ^ a b c Foster, Marcus P (5 October 2010). "The next 50 years of the SI: a review of the opportunities for the e-Science age". Metrologia. 47 (6): R41–R51. Bibcode:2010Metro..47R..41F. doi:10.1088/0026-1394/47/6/R01. S2CID 117711734. Archived from the original on 6 March 2016. Retrieved 24 June 2013.
- ^ Price, Gary (2011). "A sceptic's review of the New SI". Accreditation and Quality Assurance. 16 (3): 121–132. doi:10.1007/s00769-010-0738-x. S2CID 110127259.
- ^ Censullo, Albert C. (September–October 2011). "Part I – From the Current "Kilogram Problem" to a Proposed Definition". Chemistry International. 33 (5): 9–12. ISSN 0193-6484. Archived from the original on 9 July 2017. Retrieved 28 June 2013.
- ^ Burns, D Thorburn; Korte, EH (2013). "The Background and Implications of the "New SI" for Analytical Chemists" (PDF). Journal of the Association of Public Analysts (Online) (41 2): 28–44. Archived (PDF) from the original on 6 March 2016. Retrieved 25 June 2013.
- ^ Davis, Richard (October 2011). "Proposed change to the definition of the kilogram: Consequences for legal metrology" (PDF). OIML Bulletin. LII (4). Archived (PDF) from the original on 27 March 2015. Retrieved 28 June 2013.
- ^ Johansson, Ingvar (2011). "The Mole is Not an Ordinary Measurement Unit". Accreditation and Quality Assurance. 16 (16): 467–470. doi:10.1007/s00769-011-0804-z. S2CID 121496106.
- ^ http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf SI Brochure (8th edition)
- ^ Leonard, B.P. (2010). "Comments on recent proposals for redefining the mole and kilogram". Metrologia. 47 (3): L5–L8. Bibcode:2010Metro..47L...5L. doi:10.1088/0026-1394/47/3/L01. S2CID 118098528.
- ^ Pavese, Franco (2011). "Some reflections on the proposed redefinition of the unit for the amount of substance and of other SI units". Accreditation and Quality Assurance. 16 (3): 161–165. doi:10.1007/s00769-010-0700-y. S2CID 121598605.
- ^ Mills, Ian; Cvitaš, Tomislav; Homann, Klaus; Kallay, Nikola; Kuchitsu, Kozo (1993). Quantities, Units and Symbols in Physical Chemistry International Union of Pure and Applied Chemistry; Physical Chemistry Division (2nd ed.). International Union of Pure and Applied Chemistry, Blackwell Science Ltd. ISBN 978-0-632-03583-0.
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 114, 115, ISBN 92-822-2213-6, archived (PDF) from the original on 4 June 2021, retrieved 16 December 2021
- ^ Leonard, Brian Phillip (May 2012). "Why the dalton should be redefined exactly in terms of the kilogram". Metrologia. 49 (4): 487–491. Bibcode:2012Metro..49..487L. doi:10.1088/0026-1394/49/4/487. S2CID 55717564.
- ^ "Mise en pratique for the definition of the kelvin" (PDF). Sèvres, France: Consultative Committee for Thermometry (CCT), International Committee for Weights and Measures (CIPM). 2011. Archived (PDF) from the original on 8 May 2013. Retrieved 25 June 2013.
- ^ Consultative Committee for Thermometry (CCT) (1989). "The International Temperature Scale of 1990 (ITS-90)" (PDF). Procès-verbaux du Comité International des Poids et Mesures, 78th Meeting. Archived (PDF) from the original on 23 June 2013. Retrieved 25 June 2013.
- ^ "The International Temperature Scale of 1990 (ITS-90)" (PDF). Procès-verbaux du Comité International des Poids et Mesures, 66th Meeting (in French): 14, 143. 1977. Retrieved 1 September 2019.
Further reading
[edit]- The International System of Units (9th ed.), International Bureau of Weights and Measures, 2019, ISBN 978-92-822-2272-0
- International Bureau of Weights and Measures (BIPM) (10 August 2017). "Input data for the special CODATA-2017 adjustment". Metrologia (Updated ed.). Retrieved 14 August 2017.
External links
[edit]- BIPM website on the New SI, including a FAQ page.
- A Turning Point for Humanity: Redefining the World’s Measurement System by NIST
- Measuring Mass: The Last Artefact - BBC Four
| Base units | |
|---|---|
| Derived units with special names | |
| Other accepted units | |
| See also | |




