| Part of a series of articles about |
| Quantum mechanics |
|---|
Quantum entanglement is the phenomenon of a group of particles being generated, interacting, or sharing spatial proximity in such a way that the quantum state of each particle of the group cannot be described independently of the state of the others, including when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics.[1]
Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives rise to seemingly paradoxical effects: any measurement of a particle's properties results in an apparent and irreversible wave function collapse of that particle and changes the original quantum state. With entangled particles, such measurements affect the entangled system as a whole.
Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky, and Nathan Rosen,[2] and several papers by Erwin Schrödinger shortly thereafter,[3][4] describing what came to be known as the EPR paradox. Einstein and others considered such behavior impossible, as it violated the local realism view of causality (Einstein referring to it as "spooky action at a distance")[5] and argued that the accepted formulation of quantum mechanics must therefore be incomplete.
Later, however, the counterintuitive predictions of quantum mechanics were verified[6][7][8] in tests where polarization or spin of entangled particles were measured at separate locations, statistically violating Bell's inequality. In earlier tests, it could not be ruled out that the result at one point could have been subtly transmitted to the remote point, affecting the outcome at the second location.[8] However, so-called "loophole-free" Bell tests have since been performed where the locations were sufficiently separated that communications at the speed of light would have taken longer—in one case, 10,000 times longer—than the interval between the measurements.[7][6]
According to some interpretations of quantum mechanics, the effect of one measurement occurs instantly. Other interpretations which do not recognize wavefunction collapse dispute that there is any "effect" at all. However, all interpretations agree that entanglement produces correlation between the measurements, and that the mutual information between the entangled particles can be exploited, but that any transmission of information at faster-than-light speeds is impossible.[9][10] Thus, despite popular thought to the contrary, quantum entanglement cannot be used for faster-than-light communication.[11]
Quantum entanglement has been demonstrated experimentally with photons,[12][13] electrons,[14][15] top quarks,[16] molecules[17] and even small diamonds.[18] The use of entanglement in communication, computation and quantum radar is an active area of research and development.
History
[edit]
In 1935, Albert Einstein, Boris Podolsky and Nathan Rosen published a paper on the counterintuitive predictions that quantum mechanics makes for pairs of objects prepared together in a particular way.[2] In this study, the three formulated the Einstein–Podolsky–Rosen paradox (EPR paradox), a thought experiment that attempted to show that "the quantum-mechanical description of physical reality given by wave functions is not complete."[2] However, the three scientists did not coin the word entanglement, nor did they generalize the special properties of the quantum state they considered. Following the EPR paper, Erwin Schrödinger wrote a letter to Einstein in German in which he used the word Verschränkung (translated by himself as entanglement) "to describe the correlations between two particles that interact and then separate, as in the EPR experiment."[19] However, Schrödinger had discussed the phenomenon as early as 1932.[20]
Schrödinger shortly thereafter published a seminal paper defining and discussing the notion of "entanglement." In the paper, he recognized the importance of the concept, and stated:[3] "I would not call [entanglement] one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought." Like Einstein, Schrödinger was dissatisfied with the concept of entanglement, because it seemed to violate the speed limit on the transmission of information implicit in the theory of relativity.[21] Einstein later famously derided entanglement as "spukhafte Fernwirkung"[22] or "spooky action at a distance."
The EPR paper generated significant interest among physicists, which inspired much discussion about the foundations of quantum mechanics and Bohm's interpretation in particular, but produced relatively little other published work. Despite the interest, the weak point in EPR's argument was not discovered until 1964, when John Stewart Bell proved that one of their key assumptions, the principle of locality, as applied to the kind of hidden variables interpretation hoped for by EPR, was mathematically inconsistent with the predictions of quantum theory.
Specifically, Bell demonstrated an upper limit, seen in Bell's inequality, regarding the strength of correlations that can be produced in any theory obeying local realism, and showed that quantum theory predicts violations of this limit for certain entangled systems.[23] His inequality is experimentally testable, and there have been numerous relevant experiments, starting with the pioneering work of Stuart Freedman and John Clauser in 1972[24] and Alain Aspect's experiments in 1982.[25]
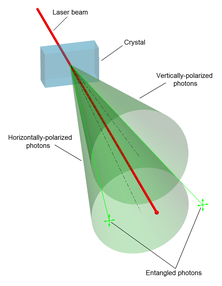
An early experimental breakthrough was due to Carl Kocher,[12][13] who already in 1967 presented an apparatus in which two photons successively emitted from a calcium atom were shown to be entangled – the first case of entangled visible light. The two photons passed diametrically positioned parallel polarizers with higher probability than classically predicted but with correlations in quantitative agreement with quantum mechanical calculations. He also showed that the correlation varied as the squared cosine of the angle between the polarizer settings[13] and decreased exponentially with time lag between emitted photons.[26] Kocher's apparatus, equipped with better polarizers, was used by Freedman and Clauser who could confirm the cosine-squared dependence and use it to demonstrate a violation of Bell's inequality for a set of fixed angles.[24] All these experiments have shown agreement with quantum mechanics rather than the principle of local realism.
For decades, each had left open at least one loophole by which it was possible to question the validity of the results. However, in 2015 an experiment was performed that simultaneously closed both the detection and locality loopholes, and was heralded as "loophole-free"; this experiment ruled out a large class of local realism theories with certainty.[27] Aspect writes that "... no experiment ... can be said to be totally loophole-free," but he says the experiments "remove the last doubts that we should renounce" local hidden variables, and refers to examples of remaining loopholes as being "far fetched" and "foreign to the usual way of reasoning in physics."[28]
Bell's work raised the possibility of using these super-strong correlations as a resource for communication. It led to the 1984 discovery of quantum key distribution protocols, most famously BB84 by Charles H. Bennett and Gilles Brassard[29] and E91 by Artur Ekert.[30] Although BB84 does not use entanglement, Ekert's protocol uses the violation of a Bell's inequality as a proof of security.
In 2022, the Nobel Prize in Physics was awarded to Alain Aspect, John Clauser, and Anton Zeilinger "for experiments with entangled photons, establishing the violation of Bell inequalities and pioneering quantum information science".[31]
Concept
[edit]Meaning of entanglement
[edit]An entangled system can be defined to be one whose quantum state cannot be factored as a product of states of its local constituents; that is to say, they are not individual particles but are an inseparable whole. In entanglement, one constituent cannot be fully described without considering the other(s). The state of a composite system is always expressible as a sum, or superposition, of products of states of local constituents; it is entangled if this sum cannot be written as a single product term.
Quantum systems can become entangled through various types of interactions. For some ways in which entanglement may be achieved for experimental purposes, see the section below on methods. Entanglement is broken when the entangled particles decohere through interaction with the environment; for example, when a measurement is made.[32]
As an example of entanglement: a subatomic particle decays into an entangled pair of other particles. The decay events obey the various conservation laws, and as a result, the measurement outcomes of one daughter particle must be highly correlated with the measurement outcomes of the other daughter particle (so that the total momenta, angular momenta, energy, and so forth remains roughly the same before and after this process). For instance, a spin-zero particle could decay into a pair of spin-1/2 particles. Since the total spin before and after this decay must be zero (conservation of angular momentum), whenever the first particle is measured to be spin up on some axis, the other, when measured on the same axis, is always found to be spin down. (This is called the spin anti-correlated case; and if the prior probabilities for measuring each spin are equal, the pair is said to be in the singlet state.)
The above result may or may not be perceived as surprising. A classical system would display the same property, and a hidden variable theory would certainly be required to do so, based on conservation of angular momentum in classical and quantum mechanics alike. The difference is that a classical system has definite values for all the observables all along, while the quantum system does not. In a sense to be discussed below, the quantum system considered here seems to acquire a probability distribution for the outcome of a measurement of the spin along any axis of the other particle upon measurement of the first particle. This probability distribution is in general different from what it would be without measurement of the first particle. This may certainly be perceived as surprising in the case of spatially separated entangled particles.
Paradox
[edit]The paradox is that a measurement made on either of the particles apparently collapses the state of the entire entangled system—and does so instantaneously, before any information about the measurement result could have been communicated to the other particle (assuming that information cannot travel faster than light) and hence assured the "proper" outcome of the measurement of the other part of the entangled pair. In the Copenhagen interpretation, the result of a spin measurement on one of the particles is a collapse (of wave function) into a state in which each particle has a definite spin (either up or down) along the axis of measurement. The outcome is taken to be random, with each possibility having a probability of 50%. However, if both spins are measured along the same axis, they are found to be anti-correlated. This means that the random outcome of the measurement made on one particle seems to have been transmitted to the other, so that it can make the "right choice" when it too is measured.[33]
The distance and timing of the measurements can be chosen so as to make the interval between the two measurements spacelike, hence, any causal effect connecting the events would have to travel faster than light. According to the principles of special relativity, it is not possible for any information to travel between two such measuring events. It is not even possible to say which of the measurements came first. For two spacelike separated events x1 and x2 there are inertial frames in which x1 is first and others in which x2 is first. Therefore, the correlation between the two measurements cannot be explained as one measurement determining the other: different observers would disagree about the role of cause and effect.
(In fact similar paradoxes can arise even without entanglement: the position of a single particle is spread out over space, and two widely separated detectors attempting to detect the particle in two different places must instantaneously attain appropriate correlation, so that they do not both detect the particle.)
Hidden variables theory
[edit]A possible resolution to the paradox is to assume that quantum theory is incomplete, and the result of measurements depends on predetermined "hidden variables".[34] The state of the particles being measured contains some hidden variables, whose values effectively determine, right from the moment of separation, what the outcomes of the spin measurements are going to be. This would mean that each particle carries all the required information with it, and nothing needs to be transmitted from one particle to the other at the time of measurement. Einstein and others (see the previous section) originally believed this was the only way out of the paradox, and the accepted quantum mechanical description (with a random measurement outcome) must be incomplete.
Violations of Bell's inequality
[edit]Local hidden variable theories fail, however, when measurements of the spin of entangled particles along different axes are considered. If a large number of pairs of such measurements are made (on a large number of pairs of entangled particles), then statistically, if the local realist or hidden variables view were correct, the results would always satisfy Bell's inequality. A number of experiments have shown in practice that Bell's inequality is not satisfied. However, prior to 2015, all of these experiments had loophole problems that were considered the most important by the community of physicists.[35][36] When measurements of the entangled particles are made in moving relativistic reference frames, in which each measurement (in its own relativistic time frame) occurs before the other, the measurement results remain correlated.[37][38]
The fundamental issue about measuring spin along different axes is that these measurements cannot have definite values at the same time―they are incompatible in the sense that these measurements' maximum simultaneous precision is constrained by the uncertainty principle. This is contrary to what is found in classical physics, where any number of properties can be measured simultaneously with arbitrary accuracy. It has been proven mathematically that compatible measurements cannot show Bell-inequality-violating correlations,[39] and thus entanglement is a fundamentally non-classical phenomenon.
Notable experimental results proving quantum entanglement
[edit]The first experiment that verified Einstein's spooky action at a distance (entanglement) was successfully corroborated in a lab by Chien-Shiung Wu and colleague I. Shaknov in 1949, and was published on New Year's Day in 1950. The result specifically proved the quantum correlations of a pair of photons.[40] In experiments in 2012 and 2013, polarization correlation was created between photons that never coexisted in time.[41][42] The authors claimed that this result was achieved by entanglement swapping between two pairs of entangled photons after measuring the polarization of one photon of the early pair, and that it proves that quantum non-locality applies not only to space but also to time.
In three independent experiments in 2013, it was shown that classically communicated separable quantum states can be used to carry entangled states.[43] The first loophole-free Bell test was held by Ronald Hanson of the Delft University of Technology in 2015, confirming the violation of Bell inequality.[44]
In August 2014, Brazilian researcher Gabriela Barreto Lemos and team were able to "take pictures" of objects using photons that had not interacted with the subjects, but were entangled with photons that did interact with such objects. Lemos, from the University of Vienna, is confident that this new quantum imaging technique could find application where low light imaging is imperative, in fields such as biological or medical imaging.[45]
Since 2016, various companies, for example IBM and Microsoft, have created quantum computers that allowed developers and tech enthusiasts to freely experiment with concepts of quantum mechanics including quantum entanglement.[46]
Emergence of time from quantum entanglement
[edit]There is a fundamental conflict, referred to as the problem of time, between the way the concept of time is used in quantum mechanics, and the role it plays in general relativity. In standard quantum theories time acts as an independent background through which states evolve, with the Hamiltonian operator acting as the generator of infinitesimal translations of quantum states through time.[47]
In contrast, general relativity treats time as a dynamical variable which relates directly with matter and moreover requires the Hamiltonian constraint to vanish. In quantized general relativity, the quantum version of the Hamiltonian constraint using metric variables, leads to the Wheeler–DeWitt equation:
where is the Hamiltonian constraint and stands for the wave function of the universe. The operator acts on the Hilbert space of wave functions, but it is not the same Hilbert space as in the nonrelativistic case. This Hamiltonian no longer determines the evolution of the system because the Schrödinger equation: , ceases to be valid. This property is known as timelessness. Various attempts to incorporate time in a fully quantum framework have been made, starting with the Page and Wootters mechanism and other subsequent proposals.[48][49]
The emergence of time was also proposed as arising from quantum correlations between an evolving system and a reference quantum clock system, the concept of system-time entanglement is introduced as a quantifier of the actual distinguishable evolution undergone by the system.[50][51] [52][53]
Emergent gravity
[edit]Based on AdS/CFT correspondence, Mark Van Raamsdonk suggested that spacetime arises as an emergent phenomenon of the quantum degrees of freedom that are entangled and live in the boundary of the spacetime.[54] Induced gravity can emerge from the entanglement first law.[55][56]
Non-locality and entanglement
[edit]In the media and popular science, quantum non-locality is often portrayed as being equivalent to entanglement. While this is true for pure bipartite quantum states, in general entanglement is only necessary for non-local correlations, but there exist mixed entangled states that do not produce such correlations.[57] A well-known example is the Werner states that are entangled for certain values of , but can always be described using local hidden variables.[58] Moreover, it was shown that, for arbitrary numbers of particles, there exist states that are genuinely entangled but admit a local model.[59]
The mentioned proofs about the existence of local models assume that there is only one copy of the quantum state available at a time. If the particles are allowed to perform local measurements on many copies of such states, then many apparently local states (e.g., the qubit Werner states) can no longer be described by a local model. This is, in particular, true for all distillable states. However, it remains an open question whether all entangled states become non-local given sufficiently many copies.[60]
Entanglement of a state shared by two particles is necessary, but not sufficient for that state to be non-local. Entanglement is more commonly viewed as an algebraic concept, noted for being a prerequisite to non-locality as well as to quantum teleportation and to superdense coding, whereas non-locality is defined according to experimental statistics and is much more involved with the foundations and interpretations of quantum mechanics.[61]
Quantum-mechanical framework
[edit]The following subsections are for those with a good working knowledge of the formal, mathematical description of quantum mechanics, including familiarity with the formalism and theoretical framework developed in the articles: bra–ket notation and mathematical formulation of quantum mechanics.
Pure states
[edit]Consider two arbitrary quantum systems A and B, with respective Hilbert spaces HA and HB. The Hilbert space of the composite system is the tensor product
If the first system is in state and the second in state , the state of the composite system is
States of the composite system that can be represented in this form are called separable states, or product states.
Not all states are separable states (and thus product states). Fix a basis for HA and a basis for HB. The most general state in HA ⊗ HB is of the form
- .
This state is separable if there exist vectors so that yielding and It is inseparable if for any vectors at least for one pair of coordinates we have If a state is inseparable, it is called an 'entangled state'.
For example, given two basis vectors of HA and two basis vectors of HB, the following is an entangled state:
If the composite system is in this state, it is impossible to attribute to either system A or system B a definite pure state. Another way to say this is that while the von Neumann entropy of the whole state is zero (as it is for any pure state), the entropy of the subsystems is greater than zero. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry.[62] The above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the HA ⊗ HB space, but which cannot be separated into pure states of each HA and HB).
Now suppose Alice is an observer for system A, and Bob is an observer for system B. If in the entangled state given above Alice makes a measurement in the eigenbasis of A, there are two possible outcomes, occurring with equal probability:[63]
- Alice measures 0, and the state of the system collapses to .
- Alice measures 1, and the state of the system collapses to .
If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system B has been altered by Alice performing a local measurement on system A. This remains true even if the systems A and B are spatially separated. This is the foundation of the EPR paradox.
The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.
Ensembles
[edit]As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has less information about the system, then one calls it an 'ensemble' and describes it by a density matrix, which is a positive-semidefinite matrix, or a trace class when the state space is infinite-dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:
where the wi are positive-valued probabilities (they sum up to 1), the vectors αi are unit vectors, and in the infinite-dimensional case, we would take the closure of such states in the trace norm. We can interpret ρ as representing an ensemble where is the proportion of the ensemble whose states are . When a mixed state has rank 1, it therefore describes a 'pure ensemble'. When there is less than total information about the state of a quantum system we need density matrices to represent the state.
Experimentally, a mixed ensemble might be realized as follows. Consider a "black box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state with spins aligned in the positive z direction, and the other with state with spins aligned in the negative y direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.
Following the definition above, for a bipartite composite system, mixed states are just density matrices on HA ⊗ HB. That is, it has the general form
where the wi are positively valued probabilities, , and the vectors are unit vectors. This is self-adjoint and positive and has trace 1.
Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as[64]: 131–132
where the wi are positively valued probabilities and the 's and 's are themselves mixed states (density operators) on the subsystems A and B respectively. In other words, a state is separable if it is a probability distribution over uncorrelated states, or product states. By writing the density matrices as sums of pure ensembles and expanding, we may assume without loss of generality that and are themselves pure ensembles. A state is then said to be entangled if it is not separable.
In general, finding out whether or not a mixed state is entangled is considered difficult. The general bipartite case has been shown to be NP-hard.[65] For the 2 × 2 and 2 × 3 cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.[66]
Reduced density matrices
[edit]The idea of a reduced density matrix was introduced by Paul Dirac in 1930.[67] Consider as above systems A and B each with a Hilbert space HA, HB. Let the state of the composite system be
As indicated above, in general there is no way to associate a pure state to the component system A. However, it still is possible to associate a density matrix. Let
- .
which is the projection operator onto this state. The state of A is the partial trace of ρT over the basis of system B:
The sum occurs over and the identity operator in . ρA is sometimes called the reduced density matrix of ρ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.
For example, the reduced density matrix of A for the entangled state
discussed above is
This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of A for the pure product state discussed above is
- .
In general, a bipartite pure state ρ is entangled if and only if its reduced states are mixed rather than pure.
Two applications that use them
[edit]Reduced density matrices were explicitly calculated in different spin chains with unique ground state. An example is the one-dimensional AKLT spin chain:[68] the ground state can be divided into a block and an environment. The reduced density matrix of the block is proportional to a projector to a degenerate ground state of another Hamiltonian.
The reduced density matrix also was evaluated for XY spin chains, where it has full rank. It was proved that in the thermodynamic limit, the spectrum of the reduced density matrix of a large block of spins is an exact geometric sequence[69] in this case.
Entanglement as a resource
[edit]In quantum information theory, entangled states are considered a 'resource', i.e., something costly to produce and that allows implementing valuable transformations.[70][71] The setting in which this perspective is most evident is that of "distant labs", i.e., two quantum systems labeled "A" and "B" on each of which arbitrary quantum operations can be performed, but which do not interact with each other quantum mechanically. The only interaction allowed is the exchange of classical information, which combined with the most general local quantum operations gives rise to the class of operations called LOCC (local operations and classical communication). These operations do not allow the production of entangled states between systems A and B. But if A and B are provided with a supply of entangled states, then these, together with LOCC operations can enable a larger class of transformations. For example, an interaction between a qubit of A and a qubit of B can be realized by first teleporting A's qubit to B, then letting it interact with B's qubit (which is now a LOCC operation, since both qubits are in B's lab) and then teleporting the qubit back to A. Two maximally entangled states of two qubits are used up in this process. Thus entangled states are a resource that enables the realization of quantum interactions (or of quantum channels) in a setting where only LOCC are available, but they are consumed in the process. There are other applications where entanglement can be seen as a resource, e.g., private communication or distinguishing quantum states.[72]
Classification of entanglement
[edit]Not all quantum states are equally valuable as a resource. To quantify this value, different entanglement measures (see below) can be used, that assign a numerical value to each quantum state. However, it is often interesting to settle for a coarser way to compare quantum states. This gives rise to different classification schemes. Most entanglement classes are defined based on whether states can be converted to other states using LOCC or a subclass of these operations. The smaller the set of allowed operations, the finer the classification. Important examples are:
- If two states can be transformed into each other by a local unitary operation, they are said to be in the same LU class. This is the finest of the usually considered classes. Two states in the same LU class have the same value for entanglement measures and the same value as a resource in the distant-labs setting. There is an infinite number of different LU classes (even in the simplest case of two qubits in a pure state).[73][74]
- If two states can be transformed into each other by local operations including measurements with probability larger than 0, they are said to be in the same 'SLOCC class' ("stochastic LOCC"). Qualitatively, two states and in the same SLOCC class are equally powerful (since I can transform one into the other and then do whatever it allows me to do), but since the transformations and may succeed with different probability, they are no longer equally valuable. E.g., for two pure qubits there are only two SLOCC classes: the entangled states (which contains both the (maximally entangled) Bell states and weakly entangled states like ) and the separable ones (i.e., product states like ).[75][76]
- Instead of considering transformations of single copies of a state (like ) one can define classes based on the possibility of multi-copy transformations. E.g., there are examples when is impossible by LOCC, but is possible. A very important (and very coarse) classification is based on the property whether it is possible to transform an arbitrarily large number of copies of a state into at least one pure entangled state. States that have this property are called distillable. These states are the most useful quantum states since, given enough of them, they can be transformed (with local operations) into any entangled state and hence allow for all possible uses. It came initially as a surprise that not all entangled states are distillable, those that are not are called 'bound entangled'.[77][72]
A different entanglement classification is based on what the quantum correlations present in a state allow A and B to do: one distinguishes three subsets of entangled states: (1) the non-local states, which produce correlations that cannot be explained by a local hidden variable model and thus violate a Bell inequality, (2) the steerable states that contain sufficient correlations for A to modify ("steer") by local measurements the conditional reduced state of B in such a way, that A can prove to B that the state they possess is indeed entangled, and finally (3) those entangled states that are neither non-local nor steerable. All three sets are non-empty.[78]
Entropy
[edit]In this section, the entropy of a mixed state is discussed as well as how it can be viewed as a measure of quantum entanglement.
Definition
[edit]
In classical information theory H, the Shannon entropy, is associated to a probability distribution, , in the following way:[79]
Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:
In general, one uses the Borel functional calculus to calculate a non-polynomial function such as log2(ρ). If the nonnegative operator ρ acts on a finite-dimensional Hilbert space and has eigenvalues , log2(ρ) turns out to be nothing more than the operator with the same eigenvectors, but the eigenvalues . The Shannon entropy is then:
- .
Since an event of probability 0 should not contribute to the entropy, and given that
the convention 0 log(0) = 0 is adopted. This extends to the infinite-dimensional case as well: if ρ has spectral resolution
assume the same convention when calculating
As in statistical mechanics, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is log(2) (which can be shown to be the maximum entropy for 2 × 2 mixed states).
As a measure of entanglement
[edit]Entropy provides one tool that can be used to quantify entanglement, although other entanglement measures exist.[80][81] If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems. For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.[82]
It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state ρ ∈ HA ⊗ HB is said to be a maximally entangled state if the reduced state of each subsystem of ρ is the diagonal matrix
For mixed states, the reduced von Neumann entropy is not the only reasonable entanglement measure.
As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics[83] (comparing the two definitions in the present context, it is customary to set the Boltzmann constant k = 1). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,
Indeed, without this property, the von Neumann entropy would not be well-defined.
In particular, U could be the time evolution operator of the system, i.e.,
where H is the Hamiltonian of the system. Here the entropy is unchanged.
Rényi entropy also can be used as a measure of entanglement.[84]
Entanglement measures
[edit]Entanglement measures quantify the amount of entanglement in a (often viewed as a bipartite) quantum state. As aforementioned, entanglement entropy is the standard measure of entanglement for pure states (but no longer a measure of entanglement for mixed states). For mixed states, there are some entanglement measures in the literature[80] and no single one is standard.
- Entanglement cost
- Distillable entanglement
- Entanglement of formation
- Concurrence
- Relative entropy of entanglement
- Squashed entanglement
- Logarithmic negativity
Most (but not all) of these entanglement measures reduce for pure states to entanglement entropy, and are difficult (NP-hard) to compute for mixed states as the dimension of the entangled system grows.[85]
Quantum field theory
[edit]The Reeh-Schlieder theorem of quantum field theory is sometimes seen as an analogue of quantum entanglement.
Applications
[edit]Entanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved.
Among the best-known applications of entanglement are superdense coding and quantum teleportation.[86]
Most researchers believe that entanglement is necessary to realize quantum computing (although this is disputed by some).[87]
Entanglement is used in some protocols of quantum cryptography,[88][89] but to prove the security of quantum key distribution (QKD) under standard assumptions does not require entanglement.[90] However, the device independent security of QKD is shown exploiting entanglement between the communication partners.[91]
Entangled states
[edit]There are several canonical entangled states that appear often in theory and experiments.
For two qubits, the Bell states are
These four pure states are all maximally entangled (according to the entropy of entanglement) and form an orthonormal basis (linear algebra) of the Hilbert space of the two qubits. They play a fundamental role in Bell's theorem.
For M>2 qubits, the GHZ state is
which reduces to the Bell state for . The traditional GHZ state was defined for . GHz states are occasionally extended to qudits, i.e., systems of d rather than 2 dimensions.
Also for M>2 qubits, there are spin squeezed states, a class of squeezed coherent states satisfying certain restrictions on the uncertainty of spin measurements, which are necessarily entangled.[92] Spin squeezed states are good candidates for enhancing precision measurements using quantum entanglement.[93]
For two bosonic modes, a NOON state is
This is like the Bell state except the basis kets 0 and 1 have been replaced with "the N photons are in one mode" and "the N photons are in the other mode".
Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a Fock state into two arms leading to a beam splitter. They are the sum of multiple of NOON states, and can be used to achieve the Heisenberg limit.[94]
For the appropriately chosen measures of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.
Methods of creating entanglement
[edit]Entanglement is usually created by direct interactions between subatomic particles. These interactions can take numerous forms. One of the most commonly used methods is spontaneous parametric down-conversion to generate a pair of photons entangled in polarization.[72][95] Other methods include the use of a fiber coupler to confine and mix photons, photons emitted from decay cascade of the bi-exciton in a quantum dot,[96] the use of the Hong–Ou–Mandel effect, etc. Quantum entanglement of a particle and its antiparticle, such as an electron and a positron, can be created by partial overlap of the corresponding quantum wave functions in Hardy's interferometer.[97][98] In the earliest tests of Bell's theorem, the entangled particles were generated using atomic cascades.[24]
It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping. Two independently prepared, identical particles may also be entangled if their wave functions merely spatially overlap, at least partially.[99]
Testing a system for entanglement
[edit]A density matrix ρ is called separable if it can be written as a convex sum of product states, namely with probabilities. By definition, a state is entangled if it is not separable.
For 2-Qubit and Qubit-Qutrit systems (2 × 2 and 2 × 3 respectively) the simple Peres–Horodecki criterion provides both a necessary and a sufficient criterion for separability, and thus—inadvertently—for detecting entanglement. However, for the general case, the criterion is merely a necessary one for separability, as the problem becomes NP-hard when generalized.[100][101] Other separability criteria include (but not limited to) the range criterion, reduction criterion, and those based on uncertainty relations.[102][103][104][105] See Ref.[106] for a review of separability criteria in discrete-variable systems and Ref.[107] for a review on techniques and challenges in experimental entanglement certification in discrete-variable systems.
A numerical approach to the problem is suggested by Jon Magne Leinaas, Jan Myrheim and Eirik Ovrum in their paper "Geometrical aspects of entanglement".[108] Leinaas et al. offer a numerical approach, iteratively refining an estimated separable state towards the target state to be tested, and checking if the target state can indeed be reached. An implementation of the algorithm (including a built-in Peres-Horodecki criterion testing) is "StateSeparator" web-app.
In continuous variable systems, the Peres-Horodecki criterion also applies. Specifically, Simon[109] formulated a particular version of the Peres-Horodecki criterion in terms of the second-order moments of canonical operators and showed that it is necessary and sufficient for -mode Gaussian states (see Ref.[110] for a seemingly different but essentially equivalent approach). It was later found[111] that Simon's condition is also necessary and sufficient for -mode Gaussian states, but no longer sufficient for -mode Gaussian states. Simon's condition can be generalized by taking into account the higher order moments of canonical operators[112][113] or by using entropic measures.[114][115]
On August 16, 2016, the world's first quantum communications satellite was launched from the Jiuquan Satellite Launch Center in China, the Quantum Experiments at Space Scale (QUESS) mission, nicknamed "Micius" after the ancient Chinese philosopher. The satellite was intended to demonstrate the feasibility of quantum communication between Earth and space, and test quantum entanglement over unprecedented distances.[116]
In the 16 June 2017, issue of Science, Yin et al. report setting a new quantum entanglement distance record of 1,203 km, demonstrating the survival of a two-photon pair and a violation of a Bell inequality, reaching a CHSH valuation of 2.37 ± 0.09, under strict Einstein locality conditions, from the Micius satellite to bases in Lijian, Yunnan and Delingha, Quinhai, increasing the efficiency of transmission over prior fiberoptic experiments by an order of magnitude.[117][118]
Naturally entangled systems
[edit]The electron shells of multi-electron atoms always consist of entangled electrons. The correct ionization energy can be calculated only by consideration of electron entanglement.[119]
Entanglement of macroscopic objects
[edit]In 2020, researchers reported the quantum entanglement between the motion of a millimeter-sized mechanical oscillator and a disparate distant spin system of a cloud of atoms.[120][121] Later work complemented this work by quantum-entangling two mechanical oscillators.[122][123][124]
Entanglement of elements of living systems
[edit]In October 2018, physicists reported producing quantum entanglement using living organisms, particularly between photosynthetic molecules within living bacteria and quantized light.[125][126]
Living organisms (green sulphur bacteria) have been studied as mediators to create quantum entanglement between otherwise non-interacting light modes, showing high entanglement between light and bacterial modes, and to some extent, even entanglement within the bacteria.[127]
See also
[edit]- Bound entanglement
- Concurrence
- CNOT gate
- Einstein's thought experiments
- Entanglement distillation
- Entanglement witness
- ER = EPR
- Faster-than-light communication
- Multipartite entanglement
- Normally distributed and uncorrelated does not imply independent
- Pauli exclusion principle
- Quantum coherence
- Quantum computing
- Quantum discord
- Quantum network
- Quantum phase transition
- Quantum pseudo-telepathy
- Quantum teleportation
- Retrocausality
- Separable state
- Spontaneous parametric down-conversion
- Squashed entanglement
- Stern–Gerlach experiment
- Ward's probability amplitude
References
[edit]- ^ Overbye, Dennis (10 October 2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe – Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times. Retrieved 10 October 2022.
- ^ a b c Einstein, Albert; Podolsky, Boris; Rosen, Nathan (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
- ^ a b Schrödinger, Erwin (1935). "Discussion of probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 31 (4): 555–563. Bibcode:1935PCPS...31..555S. doi:10.1017/S0305004100013554. S2CID 121278681.
- ^ Schrödinger, Erwin (1936). "Probability relations between separated systems". Mathematical Proceedings of the Cambridge Philosophical Society. 32 (3): 446–452. Bibcode:1936PCPS...32..446S. doi:10.1017/S0305004100019137. S2CID 122822435.
- ^ Physicist John Bell depicts the Einstein camp in this debate in his article entitled "Bertlmann's socks and the nature of reality", p. 143 of Speakable and unspeakable in quantum mechanics: "For EPR that would be an unthinkable 'spooky action at a distance'. To avoid such action at a distance they have to attribute, to the space-time regions in question, real properties in advance of observation, correlated properties, which predetermine the outcomes of these particular observations. Since these real properties, fixed in advance of observation, are not contained in quantum formalism, that formalism for EPR is incomplete. It may be correct, as far as it goes, but the usual quantum formalism cannot be the whole story." And again on p. 144 Bell says: "Einstein had no difficulty accepting that affairs in different places could be correlated. What he could not accept was that an intervention at one place could influence, immediately, affairs at the other." Downloaded 5 July 2011 from Bell, J. S. (1987). Speakable and Unspeakable in Quantum Mechanics (PDF). CERN. ISBN 0521334950. Archived from the original (PDF) on 12 April 2015. Retrieved 14 June 2014.
- ^ a b Yin, Juan; Cao, Yuan; Yong, Hai-Lin; Ren, Ji-Gang; et al. (2013). "Bounding the speed of 'spooky action at a distance". Physical Review Letters. 110 (26): 260407. arXiv:1303.0614. Bibcode:2013PhRvL.110z0407Y. doi:10.1103/PhysRevLett.110.260407. PMID 23848853. S2CID 119293698.
- ^ a b Matson, John (13 August 2012). "Quantum teleportation achieved over record distances". Nature News. doi:10.1038/nature.2012.11163. S2CID 124852641.
- ^ a b Francis, Matthew (30 October 2012). "Quantum entanglement shows that reality can't be local". Ars Technica. Retrieved 22 August 2023.
- ^ Penrose, Roger (2004). The road to reality: a complete guide to the laws of the universe. London: Jonathan Cape. p. 603. ISBN 978-0-224-04447-9.
- ^ Griffiths, David J. (2004), Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, ISBN 978-0-13-111892-8.
- ^ Siegel, Ethan. "No, We Still Can't Use Quantum Entanglement To Communicate Faster Than Light". Forbes. Retrieved 6 January 2023.
- ^ a b Kocher, C. A.; Commins, E. D. (1967). "Polarization Correlation of Photons Emitted in an Atomic Cascade". Physical Review Letters. 18 (15): 575–577. Bibcode:1967PhRvL..18..575K. doi:10.1103/PhysRevLett.18.575.
- ^ a b c Kocher, Carl Alvin (1 May 1967). Polarization Correlation of Photons Emitted in an Atomic Cascade (PhD thesis). University of California.
- ^ Hensen, B.; et al. (21 October 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. hdl:2117/79298. PMID 26503041. S2CID 205246446. See also free online access version.
- ^ Markoff, Jack (21 October 2015). "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real". The New York Times. Retrieved 21 October 2015.
- ^ "Quantum entanglement observed in top quarks". 11 October 2023.
- ^ Holland, Connor M.; Lu, Yukai; Cheuk, Lawrence W. (8 December 2023). "On-demand entanglement of molecules in a reconfigurable optical tweezer array". Science. 382 (6675): 1143–1147. arXiv:2210.06309. doi:10.1126/science.adf4272. ISSN 0036-8075.
- ^ Lee, K. C.; Sprague, M. R.; Sussman, B. J.; Nunn, J.; et al. (2 December 2011). "Entangling macroscopic diamonds at room temperature". Science. 334 (6060): 1253–1256. Bibcode:2011Sci...334.1253L. doi:10.1126/science.1211914. PMID 22144620. S2CID 206536690.
- ^ Kumar, M., Quantum, Icon Books, 2009, p. 313.
- ^ Christandl, Matthias (2006). The Structure of Bipartite Quantum States – Insights from Group Theory and Cryptography (PhD thesis). University of Cambridge. pp. vi, iv. arXiv:quant-ph/0604183. Bibcode:2006PhDT.......289C.
- ^ Alisa Bokulich, Gregg Jaeger, Philosophy of Quantum Information and Entanglement, Cambridge University Press, 2010, p. xv.
- ^ Letter from Einstein to Max Born, 3 March 1947; The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955, Walker, New York, 1971. Cited in Hobson, M. P.; et al. (1998). "Quantum Entanglement and Communication Complexity". SIAM J. Comput. 30 (6): 1829–1841. CiteSeerX 10.1.1.20.8324.)
- ^ Bell, J. S. (1964). "On the Einstein-Poldolsky-Rosen paradox". Physics Physique Физика. 1 (3): 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195.
- ^ a b c Freedman, Stuart J.; Clauser, John F. (1972). "Experimental Test of Local Hidden-Variable Theories". Physical Review Letters. 28 (14): 938–941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938.
- ^ Aspect, Alain; Grangier, Philippe; Roger, Gérard (1982). "Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Physical Review Letters. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/PhysRevLett.49.91.
- ^ Kocher, C. A. (1971). "Time correlations in the detection of successively emitted photons". Annals of Physics. 65 (1): 1–18. Bibcode:1971AnPhy..65....1K. doi:10.1016/0003-4916(71)90159-X.
- ^ Hanson, Ronald (2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041. S2CID 205246446.
- ^ Aspect, Alain (16 December 2015). "Closing the Door on Einstein and Bohr's Quantum Debate". Physics. 8: 123. Bibcode:2015PhyOJ...8..123A. doi:10.1103/Physics.8.123.
- ^ C. H. Bennett and G. Brassard. "Quantum cryptography: Public key distribution and coin tossing". In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, volume 175, p. 8. New York, 1984. http://researcher.watson.ibm.com/researcher/files/us-bennetc/BB84highest.pdf Archived 30 January 2020 at the Wayback Machine
- ^ Ekert, A.K. (1991). "Quantum cryptography based on Bell's theorem". Phys. Rev. Lett. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. ISSN 0031-9007. PMID 10044956. S2CID 27683254.
- ^ "The Nobel Prize in Physics 2022". Nobel Prize (Press release). The Royal Swedish Academy of Sciences . 4 October 2022. Retrieved 5 October 2022.
- ^ Asher Peres, Quantum Theory: Concepts and Methods, Kluwer, 1993; ISBN 0-7923-2549-4, p. 115.
- ^ Anderson, Rupert W. (28 March 2015). The Cosmic Compendium: Interstellar Travel (First ed.). The Cosmic Compendium. p. 100. ISBN 9781329022027.
- ^ Gibney, Elizabeth (2017). "Cosmic Test Bolsters Einstein's "Spooky Action at a Distance"". Scientific American.
- ^ Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Scarani, V.; Makarov, V.; Kurtsiefer, C. (2011), "Experimentally faking the violation of Bell's inequalities", Physical Review Letters, 107 (17): 170404, arXiv:1106.3224, Bibcode:2011PhRvL.107q0404G, doi:10.1103/PhysRevLett.107.170404, PMID 22107491, S2CID 16306493
- ^ Santos, E. (2004). "The failure to perform a loophole-free test of Bell's Inequality supports local realism". Foundations of Physics. 34 (11): 1643–1673. Bibcode:2004FoPh...34.1643S. doi:10.1007/s10701-004-1308-z. S2CID 123642560.
- ^ Zbinden, H.; et al. (2001). "Experimental test of nonlocal quantum correlations in relativistic configurations". Phys. Rev. A. 63 (2): 22111. arXiv:quant-ph/0007009. Bibcode:2001PhRvA..63b2111Z. doi:10.1103/PhysRevA.63.022111. S2CID 44611890.
- ^ Some of the history of both referenced Zbinden, et al. experiments is provided in Gilder, L., The Age of Entanglement, Vintage Books, 2008, pp. 321–324.
- ^ Cirel'son, B. S. (1980). "Quantum generalizations of Bell's inequality". Letters in Mathematical Physics. 4 (2): 93–100. Bibcode:1980LMaPh...4...93C. doi:10.1007/BF00417500. S2CID 120680226.
- ^ Wu, C. 's.; Shaknov, I. (1950). "The Angular Correlation of Scattered Annihilation Radiation". Physical Review. 77 (1): 136. Bibcode:1950PhRv...77..136W. doi:10.1103/PhysRev.77.136.
- ^ Ma, Xiao-song; Zotter, Stefan; Kofler, Johannes; Ursin, Rupert; Jennewein, Thomas; Brukner, Časlav; Zeilinger, Anton (26 April 2012). "Experimental delayed-choice entanglement swapping". Nature Physics. 8 (6): 480–485. arXiv:1203.4834. Bibcode:2012NatPh...8..480M. doi:10.1038/nphys2294. S2CID 119208488.
- ^ Megidish, E.; Halevy, A.; Shacham, T.; Dvir, T.; Dovrat, L.; Eisenberg, H. S. (2013). "Entanglement Swapping between Photons that have Never Coexisted". Physical Review Letters. 110 (21): 210403. arXiv:1209.4191. Bibcode:2013PhRvL.110u0403M. doi:10.1103/physrevlett.110.210403. PMID 23745845. S2CID 30063749.
- ^ "Classical carrier could create entanglement". physicsworld.com. 11 December 2013. Retrieved 14 June 2014.
- ^ "Loophole-free Bell test | Ronald Hanson". Archived from the original on 4 July 2018. Retrieved 24 October 2015.
- ^ Gibney, Elizabeth (2014). "Entangled photons make a picture from a paradox". Nature. doi:10.1038/nature.2014.15781. S2CID 124976589. Retrieved 13 October 2014.
- ^ Rozatkar, Gaurav (16 August 2018). "Demonstration of quantum entanglement". OSF.
- ^ Sakurai, J. J.; Napolitano, Jim J. (14 July 2010). Modern Quantum Mechanics (2 ed.). Pearson. p. 68. ISBN 978-0-8053-8291-4.
- ^ Page, Don N.; Wootters, William K. (15 June 1983). "Evolution without evolution: Dynamics described by stationary observables". Physical Review D. 27 (12): 2885–2892. Bibcode:1983PhRvD..27.2885P. doi:10.1103/PhysRevD.27.2885.
- ^ Rovelli, Carlo (15 October 1990). "Quantum mechanics without time: A model". Physical Review D. 42 (8): 2638–2646. Bibcode:1990PhRvD..42.2638R. doi:10.1103/PhysRevD.42.2638. PMID 10013133.
- ^ Moreva, Ekaterina (2014). "Time from quantum entanglement: an experimental illustration". Physical Review A. 89 (5): 052122. arXiv:1310.4691. Bibcode:2014PhRvA..89e2122M. doi:10.1103/PhysRevA.89.052122. S2CID 118638346.
- ^ Giovannetti, Vittorio; Lloyd, Seth; Maccone, Lorenzo (26 August 2015). "Quantum time". Physical Review D. 92 (4): 045033. arXiv:1504.04215. Bibcode:2015PhRvD..92d5033G. doi:10.1103/PhysRevD.92.045033. hdl:1721.1/98287. S2CID 85537706.
- ^ Boette, A.; Rossignoli, R.; Gigena, N.; Cerezo, M. (27 June 2016). "System-time entanglement in a discrete-time model". Physical Review A. 93 (6): 062127. arXiv:1512.07313. Bibcode:2016PhRvA..93f2127B. doi:10.1103/PhysRevA.93.062127. S2CID 119245348.
- ^ Boette, A.; Rossignoli, R. (12 September 2018). "History states of systems and operators". Physical Review A. 98 (3): 032108. arXiv:1806.00956. Bibcode:2018PhRvA..98c2108B. doi:10.1103/PhysRevA.98.032108. S2CID 56101730.
- ^ Van Raamsdonk, Mark (19 June 2010). "Building up spacetime with quantum entanglement". General Relativity and Gravitation. 42 (10): 2323–2329. arXiv:1005.3035. Bibcode:2010GReGr..42.2323V. doi:10.1007/s10714-010-1034-0. ISSN 0001-7701. S2CID 189843725.
- ^ Lee, Jae-Weon; Kim, Hyeong-Chan; Lee, Jungjai (2013). "Gravity from quantum information". Journal of the Korean Physical Society. 63 (5): 1094–1098. arXiv:1001.5445. Bibcode:2013JKPS...63.1094L. doi:10.3938/jkps.63.1094. ISSN 0374-4884. S2CID 118494859.
- ^ Swingle, Brian; Van Raamsdonk, Mark (12 May 2014). "Universality of Gravity from Entanglement". arXiv:1405.2933 [hep-th].
- ^ Brunner, Nicolas; Cavalcanti, Daniel; Pironio, Stefano; Scarani, Valerio; Wehner, Stephanie (2014). "Bell nonlocality". Reviews of Modern Physics. 86 (2): 419–478. arXiv:1303.2849. Bibcode:2014RvMP...86..419B. doi:10.1103/RevModPhys.86.419. S2CID 119194006.
- ^ Werner, R. F. (1989). "Quantum States with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model". Physical Review A. 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. PMID 9902666.
- ^ Augusiak, R.; Demianowicz, M.; Tura, J.; Acín, A. (2015). "Entanglement and nonlocality are inequivalent for any number of parties". Physical Review Letters. 115 (3): 030404. arXiv:1407.3114. Bibcode:2015PhRvL.115c0404A. doi:10.1103/PhysRevLett.115.030404. hdl:2117/78836. PMID 26230773. S2CID 29758483.
- ^ Vértesi, Tamás; Brunner, Nicolas (2014). "Disproving the Peres conjecture by showing Bell nonlocality from bound entanglement". Nature Communications. 5 (1): 5297. arXiv:1405.4502. Bibcode:2014NatCo...5.5297V. doi:10.1038/ncomms6297. PMID 25370352. S2CID 5135148.
- ^ In the literature "non-locality" is sometimes used to characterize concepts that differ from the non-existence of a local hidden variable model, e.g., whether states can be distinguished by local measurements and which can occur also for non-entangled states; see, e.g., Bennett, Charles H.; DiVincenzo, David P.; Fuchs, Christopher A.; Mor, Tal; Rains, Eric; Shor, Peter W.; Smolin, John A.; Wootters, William K. (1999). "Quantum nonlocality without entanglement". Phys. Rev. A. 59 (2): 1070–1091. arXiv:quant-ph/9804053. Bibcode:1999PhRvA..59.1070B. doi:10.1103/PhysRevA.59.1070. S2CID 15282650. This non-standard use of the term is not discussed here.
- ^ Jaeger G, Shimony A, Vaidman L (1995). "Two Interferometric Complementarities". Phys. Rev. 51 (1): 54–67. Bibcode:1995PhRvA..51...54J. doi:10.1103/PhysRevA.51.54. PMID 9911555.
- ^ Nielsen, Michael A.; Chuang, Isaac L. (2000). Quantum Computation and Quantum Information. Cambridge University Press. pp. 112–113. ISBN 978-0-521-63503-5.
- ^ Laloe, Franck (2001), "Do We Really Understand Quantum Mechanics", American Journal of Physics, 69 (6): 655–701, arXiv:quant-ph/0209123, Bibcode:2001AmJPh..69..655L, doi:10.1119/1.1356698, S2CID 123349369
- ^ Gurvits, L. (2003). "Classical deterministic complexity of Edmonds' Problem and quantum entanglement". Proceedings of the thirty-fifth annual ACM symposium on Theory of computing. p. 10. arXiv:quant-ph/0303055. doi:10.1145/780542.780545. ISBN 978-1-58113-674-6. S2CID 5745067.
- ^ Horodecki M, Horodecki P, Horodecki R (1996). "Separability of mixed states: necessary and sufficient conditions". Physics Letters A. 223 (1): 210. arXiv:quant-ph/9605038. Bibcode:1996PhLA..223....1H. CiteSeerX 10.1.1.252.496. doi:10.1016/S0375-9601(96)00706-2. S2CID 10580997.
- ^ Dirac, Paul Adrien Maurice (1930). "Note on exchange phenomena in the Thomas atom" (PDF). Mathematical Proceedings of the Cambridge Philosophical Society. 26 (3): 376–385. Bibcode:1930PCPS...26..376D. doi:10.1017/S0305004100016108.
- ^ Fan, H; Korepin V; Roychowdhury V (2004). "Entanglement in a Valence-Bond Solid State". Physical Review Letters. 93 (22): 227203. arXiv:quant-ph/0406067. Bibcode:2004PhRvL..93v7203F. doi:10.1103/PhysRevLett.93.227203. PMID 15601113. S2CID 28587190.
- ^ Franchini, F.; Its, A. R.; Korepin, V. E.; Takhtajan, L. A. (2010). "Spectrum of the density matrix of a large block of spins of the XY model in one dimension". Quantum Information Processing. 10 (3): 325–341. arXiv:1002.2931. doi:10.1007/s11128-010-0197-7. S2CID 6683370.
- ^ Chitambar, Eric; Gour, Gilad (2019). "Quantum resource theories". Reviews of Modern Physics. 91 (2): 025001. arXiv:1806.06107. Bibcode:2019RvMP...91b5001C. doi:10.1103/RevModPhys.91.025001. S2CID 119194947.
- ^ Georgiev, Danko D.; Gudder, Stanley P. (2022). "Sensitivity of entanglement measures in bipartite pure quantum states". Modern Physics Letters B. 36 (22): 2250101–2250255. arXiv:2206.13180. Bibcode:2022MPLB...3650101G. doi:10.1142/S0217984922501019. S2CID 250072286.
- ^ a b c Horodecki, Ryszard; Horodecki, Pawel; Horodecki, Michal; Horodecki, Karol (2009). "Quantum entanglement". Reviews of Modern Physics. 81 (2): 865–942. arXiv:quant-ph/0702225. Bibcode:2009RvMP...81..865H. doi:10.1103/RevModPhys.81.865. S2CID 59577352.
- ^ Grassl, M.; Rötteler, M.; Beth, T. (1998). "Computing local invariants of quantum-bit systems". Phys. Rev. A. 58 (3): 1833–1839. arXiv:quant-ph/9712040. Bibcode:1998PhRvA..58.1833G. doi:10.1103/PhysRevA.58.1833. S2CID 15892529.
- ^ Kraus, Barbara (2010). "Local unitary equivalence of multipartite pure states". Physical Review Letters. 104 (2): 020504. arXiv:0909.5152. Bibcode:2010PhRvL.104b0504K. doi:10.1103/PhysRevLett.104.020504. PMID 20366579. S2CID 29984499.
- ^ Nielsen, M. A. (1999). "Conditions for a Class of Entanglement Transformations". Physical Review Letters. 83 (2): 436. arXiv:quant-ph/9811053. Bibcode:1999PhRvL..83..436N. doi:10.1103/PhysRevLett.83.436. S2CID 17928003.
- ^ Gour, G.; Wallach, N. R. (2013). "Classification of Multipartite Entanglement of All Finite Dimensionality". Phys. Rev. Lett. 111 (6): 060502. arXiv:1304.7259. Bibcode:2013PhRvL.111f0502G. doi:10.1103/PhysRevLett.111.060502. PMID 23971544. S2CID 1570745.
- ^ Horodecki, M.; Horodecki, P.; Horodecki, R. (1998). "Mixed-state entanglement and distillation: Is there a bound entanglement in nature?". Phys. Rev. Lett. 80 (1998): 5239–5242. arXiv:quant-ph/9801069. Bibcode:1998PhRvL..80.5239H. doi:10.1103/PhysRevLett.80.5239. S2CID 111379972.
- ^ Wiseman, H. M.; Jones, S. J.; Doherty, A. C. (2007). "Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox". Physical Review Letters. 98 (14): 140402. arXiv:quant-ph/0612147. Bibcode:2007PhRvL..98n0402W. doi:10.1103/PhysRevLett.98.140402. PMID 17501251. S2CID 30078867.
- ^ Cerf, Nicolas J.; Cleve, Richard. "Information-theoretic interpretation of quantum error-correcting codes" (PDF).
- ^ a b Plenio, Martin B.; Virmani, Shashank (2007). "An introduction to entanglement measures". Quant. Inf. Comp. 1: 1–51. arXiv:quant-ph/0504163. Bibcode:2005quant.ph..4163P.
- ^ Vedral, Vlatko (2002). "The role of relative entropy in quantum information theory". Reviews of Modern Physics. 74 (1): 197–234. arXiv:quant-ph/0102094. Bibcode:2002RvMP...74..197V. doi:10.1103/RevModPhys.74.197. S2CID 6370982.
- ^ Hill, S; Wootters, W. K. (1997). "Entanglement of a Pair of Quantum Bits". Phys. Rev. Lett. 78 (26): 5022–5025. arXiv:quant-ph/9703041. Bibcode:1997PhRvL..78.5022H. doi:10.1103/PhysRevLett.78.5022. S2CID 9173232.
- ^ Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. pp. 260–270. ISBN 0-7923-2549-4. OCLC 28854083.
- ^ Wang, Yu-Xin; Mu, Liang-Zhu; Vedral, Vlatko; Fan, Heng (17 February 2016). "Entanglement Rényi α entropy". Physical Review A. 93 (2). arXiv:1504.03909. doi:10.1103/PhysRevA.93.022324. ISSN 2469-9926.
- ^ Huang, Yichen (21 March 2014). "Computing quantum discord is NP-complete". New Journal of Physics. 16 (3): 033027. arXiv:1305.5941. Bibcode:2014NJPh...16c3027H. doi:10.1088/1367-2630/16/3/033027. S2CID 118556793.
- ^ Bouwmeester, Dik; Pan, Jian-Wei; Mattle, Klaus; Eibl, Manfred; Weinfurter, Harald & Zeilinger, Anton (1997). "Experimental Quantum Teleportation" (PDF). Nature. 390 (6660): 575–579. arXiv:1901.11004. Bibcode:1997Natur.390..575B. doi:10.1038/37539. S2CID 4422887.
- ^ Jozsa, Richard; Linden, Noah (2002). "On the role of entanglement in quantum computational speed-up". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 459 (2036): 2011–2032. arXiv:quant-ph/0201143. Bibcode:2003RSPSA.459.2011J. CiteSeerX 10.1.1.251.7637. doi:10.1098/rspa.2002.1097. S2CID 15470259.
- ^ Ekert, Artur K. (1991). "Quantum cryptography based on Bell's theorem". Physical Review Letters. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. PMID 10044956. S2CID 27683254.
- ^ Yin, Juan; Yu-Huai Li; Sheng-Kai Liao; Meng Yang; Yuan Cao; Liang Zhang; Ji-Gang Ren; Wen-Qi Cai; Wei-Yue Liu; Shuang-Lin Li; Rong Shu; Yong-Mei Huang; Lei Deng; Li Li; Qiang Zhang; Nai-Le Liu; Yu-Ao Chen; Chao-Yang Lu; Xiang-Bin Wang; Feihu Xu; Jian-Yu Wang; Cheng-Zhi Peng; Artur K. Ekert; Jian-Wei Pan (2020). "Entanglement-based secure quantum cryptography over 1,120 kilometres". Nature. 582 (7813): 501–505. Bibcode:2020Natur.582..501Y. doi:10.1038/s41586-020-2401-y. PMID 32541968. S2CID 219692094.
- ^ Renner, R.; Gisin, N.; Kraus, B. (2005). "An information-theoretic security proof for QKD protocols". Physical Review A. 72: 012332. arXiv:quant-ph/0502064. doi:10.1103/PhysRevA.72.012332. S2CID 119052621.
- ^ Pirandola, S.; U. L. Andersen; L. Banchi; M. Berta; D. Bunandar; R. Colbeck; D. Englund; T. Gehring; C. Lupo; C. Ottaviani; J. L. Pereira; M. Razavi; J. Shamsul Shaari; M. Tomamichel; V. C. Usenko; G. Vallone; P. Villoresi; P. Wallden (2020). "Advances in quantum cryptography". Adv. Opt. Photon. 12 (4): 1012–1236. arXiv:1906.01645. Bibcode:2020AdOP...12.1012P. doi:10.1364/AOP.361502. S2CID 174799187.
- ^ Kitagawa, Masahiro; Ueda, Masahito (1993). "Squeezed Spin States" (PDF). Physical Review A. 47 (6): 5138–5143. Bibcode:1993PhRvA..47.5138K. doi:10.1103/physreva.47.5138. hdl:11094/77656. PMID 9909547.
- ^ Wineland, D. J.; Bollinger, J. J.; Itano, W. M.; Moore, F. L.; Heinzen, D. J. (1992). "Spin squeezing and reduced quantum noise in spectroscopy". Physical Review A. 46 (11): R6797–R6800. Bibcode:1992PhRvA..46.6797W. doi:10.1103/PhysRevA.46.R6797. PMID 9908086.
- ^ Holland, M. J; Burnett, K (1993). "Interferometric detection of optical phase shifts at the Heisenberg limit". Physical Review Letters. 71 (9): 1355–1358. Bibcode:1993PhRvL..71.1355H. doi:10.1103/PhysRevLett.71.1355. PMID 10055519.
- ^ Shadbolt, P. J.; Verde, M. R.; Peruzzo, A.; Politi, A.; Laing, A.; Lobino, M.; Matthews, J. C. F.; Thompson, M. G.; O'Brien, J. L. (2012). "Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit". Nature Photonics. 6 (1): 45–59. arXiv:1108.3309. Bibcode:2012NaPho...6...45S. doi:10.1038/nphoton.2011.283. S2CID 56206588.
- ^ Akopian, N. (2006). "Entangled Photon Pairs from Semiconductor Quantum Dots". Physical Review Letters. 96 (2): 130501. arXiv:quant-ph/0509060. Bibcode:2006PhRvL..96b0501D. doi:10.1103/PhysRevLett.96.020501. PMID 16486553. S2CID 22040546.
- ^ Hardy, Lucien (1992). "Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories". Physical Review Letters. 68 (20): 2981–2984. Bibcode:1992PhRvL..68.2981H. doi:10.1103/PhysRevLett.68.2981. PMID 10045577.
- ^ Georgiev, Danko; Cohen, Eliahu (2022). "Entanglement measures for two-particle quantum histories". Physical Review A. 106 (6): 062437. arXiv:2212.07502. Bibcode:2022PhRvA.106f2437G. doi:10.1103/PhysRevA.106.062437. S2CID 254685902.
- ^ Lo Franco, Rosario; Compagno, Giuseppe (14 June 2018). "Indistinguishability of Elementary Systems as a Resource for Quantum Information Processing". Physical Review Letters. 120 (24): 240403. arXiv:1712.00706. Bibcode:2018PhRvL.120x0403L. doi:10.1103/PhysRevLett.120.240403. PMID 29957003. S2CID 49562954.
- ^ Gurvits, L., Classical deterministic complexity of Edmonds' problem and quantum entanglement, in Proceedings of the 35th ACM Symposium on Theory of Computing, ACM Press, New York, 2003.
- ^ Gharibian, Sevag (2010). "Strong NP-Hardness of the Quantum Separability Problem". Quantum Information and Computation. 10 (3&4): 343–360. arXiv:0810.4507. doi:10.26421/QIC10.3-4-11. S2CID 621887.
- ^ Hofmann, Holger F.; Takeuchi, Shigeki (22 September 2003). "Violation of local uncertainty relations as a signature of entanglement". Physical Review A. 68 (3): 032103. arXiv:quant-ph/0212090. Bibcode:2003PhRvA..68c2103H. doi:10.1103/PhysRevA.68.032103. S2CID 54893300.
- ^ Gühne, Otfried (18 March 2004). "Characterizing Entanglement via Uncertainty Relations". Physical Review Letters. 92 (11): 117903. arXiv:quant-ph/0306194. Bibcode:2004PhRvL..92k7903G. doi:10.1103/PhysRevLett.92.117903. PMID 15089173. S2CID 5696147.
- ^ Gühne, Otfried; Lewenstein, Maciej (24 August 2004). "Entropic uncertainty relations and entanglement". Physical Review A. 70 (2): 022316. arXiv:quant-ph/0403219. Bibcode:2004PhRvA..70b2316G. doi:10.1103/PhysRevA.70.022316. S2CID 118952931.
- ^ Huang, Yichen (29 July 2010). "Entanglement criteria via concave-function uncertainty relations". Physical Review A. 82 (1): 012335. Bibcode:2010PhRvA..82a2335H. doi:10.1103/PhysRevA.82.012335.
- ^ Gühne, Otfried; Tóth, Géza (2009). "Entanglement detection". Physics Reports. 474 (1–6): 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004. S2CID 119288569.
- ^ Friis, Nicolai; Vitagliano, Giuseppe; Malik, Mehul; Huber, Marcus (2019). "Entanglement certification from theory to experiment". Nature Reviews Physics. 1: 72–87. arXiv:1906.10929. doi:10.1038/s42254-018-0003-5. ISSN 2522-5820. S2CID 125658647.
- ^ Leinaas, Jon Magne; Myrheim, Jan; Ovrum, Eirik (2006). "Geometrical aspects of entanglement". Physical Review A. 74 (1): 012313. arXiv:quant-ph/0605079. Bibcode:2006PhRvA..74a2313L. doi:10.1103/PhysRevA.74.012313. S2CID 119443360.
- ^ Simon, R. (2000). "Peres-Horodecki Separability Criterion for Continuous Variable Systems". Physical Review Letters. 84 (12): 2726–2729. arXiv:quant-ph/9909044. Bibcode:2000PhRvL..84.2726S. doi:10.1103/PhysRevLett.84.2726. PMID 11017310. S2CID 11664720.
- ^ Duan, Lu-Ming; Giedke, G.; Cirac, J. I.; Zoller, P. (2000). "Inseparability Criterion for Continuous Variable Systems". Physical Review Letters. 84 (12): 2722–2725. arXiv:quant-ph/9908056. Bibcode:2000PhRvL..84.2722D. doi:10.1103/PhysRevLett.84.2722. PMID 11017309. S2CID 9948874.
- ^ Werner, R. F.; Wolf, M. M. (2001). "Bound Entangled Gaussian States". Physical Review Letters. 86 (16): 3658–3661. arXiv:quant-ph/0009118. Bibcode:2001PhRvL..86.3658W. doi:10.1103/PhysRevLett.86.3658. PMID 11328047. S2CID 20897950.
- ^ Shchukin, E.; Vogel, W. (2005). "Inseparability Criteria for Continuous Bipartite Quantum States". Physical Review Letters. 95 (23): 230502. arXiv:quant-ph/0508132. Bibcode:2005PhRvL..95w0502S. doi:10.1103/PhysRevLett.95.230502. PMID 16384285. S2CID 28595936.
- ^ Hillery, Mark; Zubairy, M.Suhail (2006). "Entanglement Conditions for Two-Mode States". Physical Review Letters. 96 (5): 050503. arXiv:quant-ph/0507168. Bibcode:2006PhRvL..96e0503H. doi:10.1103/PhysRevLett.96.050503. PMID 16486912. S2CID 43756465.
- ^ Walborn, S.; Taketani, B.; Salles, A.; Toscano, F.; de Matos Filho, R. (2009). "Entropic Entanglement Criteria for Continuous Variables". Physical Review Letters. 103 (16): 160505. arXiv:0909.0147. Bibcode:2009PhRvL.103p0505W. doi:10.1103/PhysRevLett.103.160505. PMID 19905682. S2CID 10523704.
- ^ Huang, Yichen (October 2013). "Entanglement Detection: Complexity and Shannon Entropic Criteria". IEEE Transactions on Information Theory. 59 (10): 6774–6778. doi:10.1109/TIT.2013.2257936. S2CID 7149863.
- ^ "China launches world's first quantum science satellite". physicsworld.com. 16 August 2016. Retrieved 7 December 2021.
- ^ Yin, Juan; Cao, Yuan; Li, Yu-Huai; Liao, Sheng-Kai; et al. (2017). "Satellite-based entanglement distribution over 1200 kilometers". Science. 356 (6343): 1140–1144. arXiv:1707.01339. doi:10.1126/science.aan3211. PMID 28619937.
- ^ "China's quantum satellite achieves 'spooky action' at record distance". 14 June 2017.
- ^ Frank Jensen: Introduction to Computational Chemistry. Wiley, 2007, ISBN 978-0-470-01187-4.
- ^ "Quantum entanglement realized between distant large objects". phys.org. Retrieved 9 October 2020.
- ^ Thomas, Rodrigo A.; Parniak, Michał; Østfeldt, Christoffer; Møller, Christoffer B.; et al. (21 September 2020). "Entanglement between distant macroscopic mechanical and spin systems". Nature Physics. 17 (2): 228–233. arXiv:2003.11310. doi:10.1038/s41567-020-1031-5. ISSN 1745-2481. S2CID 214641162. Retrieved 9 October 2020.
- ^ "Vibrating drumheads are entangled quantum mechanically". Physics World. 17 May 2021. Retrieved 14 June 2021.
- ^ Lépinay, Laure Mercier de; Ockeloen-Korppi, Caspar F.; Woolley, Matthew J.; Sillanpää, Mika A. (7 May 2021). "Quantum mechanics–free subsystem with mechanical oscillators". Science. 372 (6542): 625–629. arXiv:2009.12902. Bibcode:2021Sci...372..625M. doi:10.1126/science.abf5389. ISSN 0036-8075. PMID 33958476. S2CID 221971015. Retrieved 14 June 2021.
- ^ Kotler, Shlomi; Peterson, Gabriel A.; Shojaee, Ezad; Lecocq, Florent; et al. (7 May 2021). "Direct observation of deterministic macroscopic entanglement". Science. 372 (6542): 622–625. arXiv:2004.05515. Bibcode:2021Sci...372..622K. doi:10.1126/science.abf2998. ISSN 0036-8075. PMID 33958475. S2CID 233872863. Retrieved 14 June 2021.
- ^ Marletto, C.; Coles, D. M.; Farrow, T.; Vedral, V. (2018). "Entanglement between living bacteria and quantized light witnessed by Rabi splitting". Journal of Physics Communications. 2 (10): 101001. arXiv:1702.08075. Bibcode:2018JPhCo...2j1001M. doi:10.1088/2399-6528/aae224. S2CID 119236759.
- ^ O'Callaghan, Jonathan (29 October 2018). ""Schrödinger's Bacterium" Could Be a Quantum Biology Milestone – A recent experiment may have placed living organisms in a state of quantum entanglement". Scientific American. Retrieved 29 October 2018.
- ^ Krisnanda, T.; Marletto, C.; Vedral, V.; Paternostro, M.; Paterek, T. (2018). "Probing quantum features of photosynthetic organisms". npj Quantum Information. 4: 60. arXiv:1711.06485. Bibcode:2018npjQI...4...60K. doi:10.1038/s41534-018-0110-2.
Further reading
[edit]- Albert, David Z.; Galchen, Rivka (2009). "Was Einstein Wrong?: A Quantum Threat to Special Relativity". Scientific American. 300 (3): 32–39. doi:10.1038/scientificamerican0309-32. PMID 19253771.
- Bengtsson I.; Życzkowski K. (2006). "Geometry of Quantum States". An Introduction to Quantum Entanglement. Cambridge: Cambridge University Press. second, revised edition (2017)
- Bub, Jeffrey (2019). "Quantum Entanglement and Information". Stanford Encyclopedia of Philosophy. Stanford, California: Stanford University.
- Cramer JG (2015). The Quantum Handshake: Entanglement, Nonlocality and Transactions. Springer Verlag. ISBN 978-3-319-24642-0.
- Duarte FJ (2019). Fundamentals of Quantum Entanglement. Bristol, UK: Institute of Physics. ISBN 978-0-7503-2226-3.
- Gühne O, Tóth G (2009). "Entanglement detection". Physics Reports. 474 (1–6): 1–75. arXiv:0811.2803. Bibcode:2009PhR...474....1G. doi:10.1016/j.physrep.2009.02.004. S2CID 119288569.
- Bhaskara VS, Panigrahi PK (2017). "Generalized concurrence measure for faithful quantification of multiparticle pure state entanglement using Lagrange's identity and wedge product". Quantum Information Processing. 16 (5): 118. arXiv:1607.00164. Bibcode:2017QuIP...16..118B. doi:10.1007/s11128-017-1568-0. S2CID 43754114.
- Swain SN, Bhaskara VS, Panigrahi PK (2022). "Generalized entanglement measure for continuous-variable systems". Phys. Rev. A. 105 (5): 052441. arXiv:1706.01448. Bibcode:2022PhRvA.105e2441S. doi:10.1103/PhysRevA.105.052441. S2CID 239885759.
- Jaeger G (2009). Entanglement, Information, and the Interpretation of Quantum Mechanics. Heildelberg: Springer. ISBN 978-3-540-92127-1.
- Steward EG (2008). Quantum Mechanics: Its Early Development and the Road to Entanglement. Imperial College Press. ISBN 978-1-86094-978-4.
External links
[edit]- Explanatory video by Scientific American magazine
- Entanglement experiment with photon pairs – interactive
- Audio – Cain/Gay (2009) Astronomy Cast Entanglement
- "Spooky Actions at a Distance?": Oppenheimer Lecture, Prof. David Mermin (Cornell University) Univ. California, Berkeley, 2008. Non-mathematical popular lecture on YouTube, posted Mar 2008
- "Quantum Entanglement versus Classical Correlation" (Interactive demonstration)
| International | |
|---|---|
| National | |
| Other | |














![{\displaystyle [c_{i}^{A}],[c_{j}^{B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2b47f980dac5bc92f73609aef7a6280f2f2be7f)
















![{\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c))_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf2f7c56adc4e273d3e3c73ee6a66e190c3f35c)














































