
|

|

|
|

|

|

|

|
|

|

|
|

|

|

|

|
|

|
|

|
In geometry, the term semiregular polyhedron (or semiregular polytope) is used variously by different authors.

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
In geometry, the term semiregular polyhedron (or semiregular polytope) is used variously by different authors.
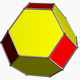
In its original definition, it is a polyhedron with regular polygonal faces, and a symmetry group which is transitive on its vertices; today, this is more commonly referred to as a uniform polyhedron (this follows from Thorold Gosset's 1900 definition of the more general semiregular polytope).[1][2] These polyhedra include:
These semiregular solids can be fully specified by a vertex configuration: a listing of the faces by number of sides, in order as they occur around a vertex. For example: 3.5.3.5 represents the icosidodecahedron, which alternates two triangles and two pentagons around each vertex. In contrast: 3.3.3.5 is a pentagonal antiprism. These polyhedra are sometimes described as vertex-transitive.
Since Gosset, other authors have used the term semiregular in different ways in relation to higher dimensional polytopes. E. L. Elte[3] provided a definition which Coxeter found too artificial. Coxeter himself dubbed Gosset's figures uniform, with only a quite restricted subset classified as semiregular.[4]
Yet others have taken the opposite path, categorising more polyhedra as semiregular. These include:
A further source of confusion lies in the way that the Archimedean solids are defined, again with different interpretations appearing.
Gosset's definition of semiregular includes figures of higher symmetry: the regular and quasiregular polyhedra. Some later authors prefer to say that these are not semiregular, because they are more regular than that - the uniform polyhedra are then said to include the regular, quasiregular, and semiregular ones. This naming system works well, and reconciles many (but by no means all) of the confusions.
In practice even the most eminent authorities can get themselves confused, defining a given set of polyhedra as semiregular and/or Archimedean, and then assuming (or even stating) a different set in subsequent discussions. Assuming that one's stated definition applies only to convex polyhedra is probably the most common failing. Coxeter, Cromwell,[5] and Cundy & Rollett[6] are all guilty of such slips.
Trigonal trapezohedron (V(3.3)2) |
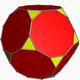
 Rhombic dodecahedron V(3.4)2 |
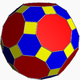
 Rhombic triacontahedron V(3.5)2 |
Johannes Kepler coined the category semiregular in his book Harmonices Mundi (1619), including the 13 Archimedean solids, two infinite families (prisms and antiprisms on regular bases), and two edge-transitive Catalan solids, the rhombic dodecahedron and rhombic triacontahedron. He also considered a rhombus as a semiregular polygon (being equilateral and alternating two angles) as well as star polygons, now called isotoxal figures which he used in planar tilings. The trigonal trapezohedron, a topological cube with congruent rhombic faces, would also qualify as semiregular, though Kepler did not mention it specifically.
In many works semiregular polyhedron is used as a synonym for Archimedean solid.[7] For example, Cundy & Rollett (1961).
We can distinguish between the facially-regular and vertex-transitive figures based on Gosset, and their vertically-regular (or versi-regular) and facially-transitive duals.
Coxeter et al. (1954) use the term semiregular polyhedra to classify uniform polyhedra with Wythoff symbol of the form p q | r, a definition encompassing only six of the Archimedean solids, as well as the regular prisms (but not the regular antiprisms) and numerous nonconvex solids. Later, Coxeter (1973) would quote Gosset's definition without comment, thus accepting it by implication.
Eric Weisstein, Robert Williams and others use the term to mean the convex uniform polyhedra excluding the five regular polyhedra – including the Archimedean solids, the uniform prisms, and the uniform antiprisms (overlapping with the cube as a prism and regular octahedron as an antiprism).[8][9]
Peter Cromwell (1997) writes in a footnote to Page 149 that, "in current terminology, 'semiregular polyhedra' refers to the Archimedean and Catalan (Archimedean dual) solids". On Page 80 he describes the thirteen Archimedeans as semiregular, while on Pages 367 ff. he discusses the Catalans and their relationship to the 'semiregular' Archimedeans. By implication this treats the Catalans as not semiregular, thus effectively contradicting (or at least confusing) the definition he provided in the earlier footnote. He ignores nonconvex polyhedra.