| 3D honeycombs | ||
|---|---|---|
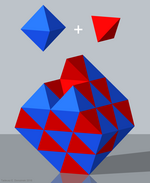 Simple tetroctahedric check |
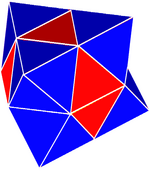 Complex tetroctahedric check | |
| 4D polytopes | ||
 Tetroctahedric |
 Octicosahedric |
 Tetricosahedric |
In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as The Semiregular Polytopes of the Hyperspaces which included a wider definition.
In three-dimensional space and below, the terms semiregular polytope and uniform polytope have identical meanings, because all uniform polygons must be regular. However, since not all uniform polyhedra are regular, the number of semiregular polytopes in dimensions higher than three is much smaller than the number of uniform polytopes in the same number of dimensions.
The three convex semiregular 4-polytopes are the rectified 5-cell, snub 24-cell and rectified 600-cell. The only semiregular polytopes in higher dimensions are the k21 polytopes, where the rectified 5-cell is the special case of k = 0. These were all listed by Gosset, but a proof of the completeness of this list was not published until the work of Makarov (1988) for four dimensions, and Blind & Blind (1991) for higher dimensions.

Semiregular polytopes can be extended to semiregular honeycombs. The semiregular Euclidean honeycombs are the tetrahedral-octahedral honeycomb (3D), gyrated alternated cubic honeycomb (3D) and the 521 honeycomb (8D).
Gosset honeycombs:
Semiregular E-honeycomb:
Gosset (1900) additionally allowed Euclidean honeycombs as facets of higher-dimensional Euclidean honeycombs, giving the following additional figures:

There are also hyperbolic uniform honeycombs composed of only regular cells (Coxeter & Whitrow 1950), including: