Generalization of category
In category theory, a strict 2-category is a category with "morphisms between morphisms", that is, where each hom-set itself carries the structure of a category. It can be formally defined as a category enriched over Cat (the category of categories and functors, with the monoidal structure given by product of categories).
The concept of 2-category was first introduced by Charles Ehresmann in his work on enriched categories in 1965.[1] The more general concept of bicategory (or weak 2-category), where composition of morphisms is associative only up to a 2-isomorphism, was introduced in 1968 by Jean Bénabou.[2]
Definition
A 2-category C consists of:
- A class of 0-cells (or objects) A, B, ....
- For all objects A and B, a category
 . The objects
. The objects  of this category are called 1-cells and its morphisms
of this category are called 1-cells and its morphisms  are called 2-cells; the composition in this category is usually written
are called 2-cells; the composition in this category is usually written  or
or  and called vertical composition or composition along a 1-cell.
and called vertical composition or composition along a 1-cell.
- For any object A there is a functor from the terminal category (with one object and one arrow) to
 that picks out the identity 1-cell idA on A and its identity 2-cell ididA. In practice these two are often denoted simply by A.
that picks out the identity 1-cell idA on A and its identity 2-cell ididA. In practice these two are often denoted simply by A.
- For all objects A, B and C, there is a functor
 , called horizontal composition or composition along a 0-cell, which is associative and admits[clarification needed] the identity 1 and 2-cells of idA as identities. Here, associativity for
, called horizontal composition or composition along a 0-cell, which is associative and admits[clarification needed] the identity 1 and 2-cells of idA as identities. Here, associativity for  means that horizontally composing
means that horizontally composing  twice to
twice to  is independent of which of the two
is independent of which of the two  and
and  are composed first. The composition symbol
are composed first. The composition symbol  is often omitted, the horizontal composite of 2-cells
is often omitted, the horizontal composite of 2-cells  and
and  being written simply as
being written simply as  .
.
The 0-cells, 1-cells, and 2-cells terminology is replaced by 0-morphisms, 1-morphisms, and 2-morphisms in some sources[3] (see also Higher category theory).
The notion of 2-category differs from the more general notion of a bicategory in that composition of 1-cells (horizontal composition) is required to be strictly associative, whereas in a bicategory it needs only be associative up to a 2-isomorphism. The axioms of a 2-category are consequences of their definition as Cat-enriched categories:
- Vertical composition is associative and unital, the units being the identity 2-cells idf.
- Horizontal composition is also (strictly) associative and unital, the units being the identity 2-cells ididA on the identity 1-cells idA.
- The interchange law holds; i.e. it is true that for composable 2-cells


The interchange law follows from the fact that  is a functor between hom categories. It can be drawn as a pasting diagram as follows:
is a functor between hom categories. It can be drawn as a pasting diagram as follows:
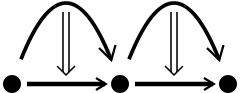
|
=
|

|
=
|

|

|

|

|

|
Here the left-hand diagram denotes the vertical composition of horizontal composites, the right-hand diagram denotes the horizontal composition of vertical composites, and the diagram in the centre is the customary representation of both. The 2-cell are drawn with double arrows ⇒, the 1-cell with single arrows →, and the 0-cell with points.
Examples
The category Ord (of preordered sets) is a 2-category since preordered sets can easily be interpreted as categories.
Category of small categories
The archetypal 2-category is the category of small categories, with natural transformations serving as 2-morphisms; typically 2-morphisms are given by Greek letters (such as  above) for this reason.
above) for this reason.
The objects (0-cells) are all small categories, and for all objects A and B the category  is a functor category. In this context, vertical composition is[4] the composition of natural transformations.
is a functor category. In this context, vertical composition is[4] the composition of natural transformations.
Doctrines
In mathematics, a doctrine is simply a 2-category which is heuristically regarded as a system of theories. For example, algebraic theories, as invented by William Lawvere, is an example of a doctrine, as are multi-sorted theories, operads, categories, and toposes.
The objects of the 2-category are called theories, the 1-morphisms  are called models of the A in B, and the 2-morphisms are called morphisms between models.
are called models of the A in B, and the 2-morphisms are called morphisms between models.
The distinction between a 2-category and a doctrine is really only heuristic: one does not typically consider a 2-category to be populated by theories as objects and models as morphisms. It is this vocabulary that makes the theory of doctrines worth while.
For example, the 2-category Cat of categories, functors, and natural transformations is a doctrine. One sees immediately that all presheaf categories are categories of models.
As another example, one may take the subcategory of Cat consisting only of categories with finite products as objects and product-preserving functors as 1-morphisms. This is the doctrine of multi-sorted algebraic theories. If one only wanted 1-sorted algebraic theories, one would restrict the objects to only those categories that are generated under products by a single object.
Doctrines were discovered by Jonathan Mock Beck.
























