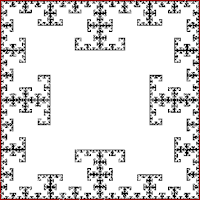
In mathematics, the T-square is a two-dimensional fractal. It has a boundary of infinite length bounding a finite area. Its name comes from the drawing instrument known as a T-square.[1]
In mathematics, the T-square is a two-dimensional fractal. It has a boundary of infinite length bounding a finite area. Its name comes from the drawing instrument known as a T-square.[1]

It can be generated from using this algorithm:

The method of creation is rather similar to the ones used to create a Koch snowflake or a Sierpinski triangle, "both based on recursively drawing equilateral triangles and the Sierpinski carpet."[1]
The T-square fractal has a fractal dimension of ln(4)/ln(2) = 2.[citation needed] The black surface extent is almost everywhere in the bigger square, for once a point has been darkened, it remains black for every other iteration; however some points remain white.
The fractal dimension of the boundary equals .
Using mathematical induction one can prove that for each n ≥ 2 the number of new squares that are added at stage n equals .
The T-square fractal can also be generated by an adaptation of the chaos game, in which a point jumps repeatedly half-way towards the randomly chosen vertices of a square. The T-square appears when the jumping point is unable to target the vertex directly opposite the vertex previously chosen. That is, if the current vertex is v[i] and the previous vertex was v[i-1], then v[i] ≠ v[i-1] + vinc, where vinc = 2 and modular arithmetic means that 3 + 2 = 1, 4 + 2 = 2:
If vinc is given different values, allomorphs of the T-square appear that are computationally equivalent to the T-square but very different in appearance:
 |
 |
The T-square fractal can be derived from the Sierpiński triangle, and vice versa, by adjusting the angle at which sub-elements of the original fractal are added from the center outwards.
 |