Definition
The blancmange function is defined on the unit interval by

where  is the triangle wave, defined by
is the triangle wave, defined by  ,
that is,
,
that is,  is the distance from x to the nearest integer.
is the distance from x to the nearest integer.
The Takagi–Landsberg curve is a slight generalization, given by

for a parameter  ; thus the blancmange curve is the case
; thus the blancmange curve is the case  . The value
. The value  is known as the Hurst parameter.
is known as the Hurst parameter.
The function can be extended to all of the real line: applying the definition given above shows that the function repeats on each unit interval.
Functional equation definition
The periodic version of the Takagi curve can also be defined as the unique bounded solution  to the functional equation
to the functional equation

Indeed, the blancmange function  is certainly bounded, and solves the functional equation, since
is certainly bounded, and solves the functional equation, since


Conversely, if  is a bounded solution of the functional equation, iterating the equality one has for any N
is a bounded solution of the functional equation, iterating the equality one has for any N

whence  . Incidentally, the above functional equations possesses infinitely many continuous, non-bounded solutions, e.g.
. Incidentally, the above functional equations possesses infinitely many continuous, non-bounded solutions, e.g.

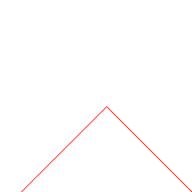
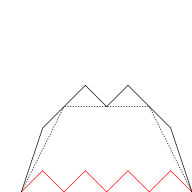
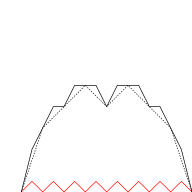
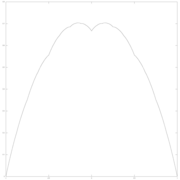
Graphical construction
The blancmange curve can be visually built up out of triangle wave functions if the infinite sum is approximated by finite sums of the first few terms. In the illustrations below, progressively finer triangle functions (shown in red) are added to the curve at each stage.
Properties
Convergence and continuity
The infinite sum defining  converges absolutely for all
converges absolutely for all  Since
Since  for all
for all 

if  The Takagi curve of parameter
The Takagi curve of parameter  is defined on the unit interval (or
is defined on the unit interval (or  ) if
) if  . The Takagi function of parameter
. The Takagi function of parameter  is continuous. The functions
is continuous. The functions  defined by the partial sums
defined by the partial sums

are continuous and converge uniformly toward 

for all x when  This bound decreases as
This bound decreases as  By the uniform limit theorem,
By the uniform limit theorem,  is continuous if |w| < 1.
is continuous if |w| < 1.
-
parameter w = 2/3
-
parameter w = 1/2
-
parameter w = 1/3
-
parameter w = 1/4
-
parameter w = 1/8
Subadditivity
Since the absolute value is a subadditive function so is the function  , and its dilations
, and its dilations  ; since positive linear combinations and point-wise limits of subadditive functions are subadditive, the Takagi function is subadditive for any value of the parameter
; since positive linear combinations and point-wise limits of subadditive functions are subadditive, the Takagi function is subadditive for any value of the parameter  .
.
The special case of the parabola
For  , one obtains the parabola: the construction of the parabola by midpoint subdivision was described by Archimedes.
, one obtains the parabola: the construction of the parabola by midpoint subdivision was described by Archimedes.
Differentiability
For values of the parameter  the Takagi function
the Takagi function  is differentiable in the classical sense at any
is differentiable in the classical sense at any  which is not a dyadic rational. By derivation under the sign of series, for any non dyadic rational
which is not a dyadic rational. By derivation under the sign of series, for any non dyadic rational  one finds
one finds

where  is the sequence of binary digits in the base 2 expansion of
is the sequence of binary digits in the base 2 expansion of  :
:

Equivalently, the bits in the binary expansion can be understood as a sequence of square waves, the Haar wavelets, scaled to width  This follows, since the derivative of the triangle wave is just the square wave:
This follows, since the derivative of the triangle wave is just the square wave:

and so

For the parameter  the function
the function  is Lipschitz of constant
is Lipschitz of constant  In particular for the special value
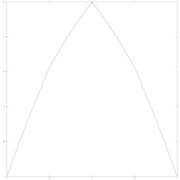
In particular for the special value  one finds, for any non dyadic rational
one finds, for any non dyadic rational ![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)
 , according with the mentioned
, according with the mentioned 
For  the blancmange function
the blancmange function  it is of bounded variation on no non-empty open set; it is not even locally Lipschitz, but it is quasi-Lipschitz, indeed, it admits the function
it is of bounded variation on no non-empty open set; it is not even locally Lipschitz, but it is quasi-Lipschitz, indeed, it admits the function  as a modulus of continuity .
as a modulus of continuity .
Fourier series expansion
The Takagi–Landsberg function admits an absolutely convergent Fourier series expansion:

with  and, for
and, for 

where  is the maximum power of
is the maximum power of  that divides
that divides  .
Indeed, the above triangle wave
.
Indeed, the above triangle wave  has an absolutely convergent Fourier series expansion
has an absolutely convergent Fourier series expansion

By absolute convergence, one can reorder the corresponding double series for  :
:

putting  yields the above Fourier series for
yields the above Fourier series for 
Self similarity
The recursive definition allows the monoid of self-symmetries of the curve to be given. This monoid is given by two generators, g and r, which act on the curve (restricted to the unit interval) as
=T_{w}\left(g\cdot x\right)=T_{w}\left({\frac {x}{2))\right)={\frac {x}{2))+wT_{w}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80f034a1c5a31e0450f85eeddfb63b70991e300f)
and
=T_{w}(r\cdot x)=T_{w}(1-x)=T_{w}(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288657b954a7fa30be7fc8ce85bfb6e11c5da16b)
A general element of the monoid then has the form  for some integers
for some integers  This acts on the curve as a linear function:
This acts on the curve as a linear function:  for some constants a, b and c. Because the action is linear, it can be described in terms of a vector space, with the vector space basis:
for some constants a, b and c. Because the action is linear, it can be described in terms of a vector space, with the vector space basis:



In this representation, the action of g and r are given by

and

That is, the action of a general element  maps the blancmange curve on the unit interval [0,1] to a sub-interval
maps the blancmange curve on the unit interval [0,1] to a sub-interval ![{\displaystyle [m/2^{p},n/2^{p}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2acb3583829325eec7ea50efa165a45b3385898) for some integers m, n, p. The mapping is given exactly by
for some integers m, n, p. The mapping is given exactly by =a+bx+cT_{w}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/932dcafe233d050f126f04a32d13dee690b55c6d) where the values of a, b and c can be obtained directly by multiplying out the above matrices. That is:
where the values of a, b and c can be obtained directly by multiplying out the above matrices. That is:

Note that  is immediate.
is immediate.
The monoid generated by g and r is sometimes called the dyadic monoid; it is a sub-monoid of the modular group. When discussing the modular group, the more common notation for g and r is T and S, but that notation conflicts with the symbols used here.
The above three-dimensional representation is just one of many representations it can have; it shows that the blancmange curve is one possible realization of the action. That is, there are representations for any dimension, not just 3; some of these give the de Rham curves.
Integrating the Blancmange curve
Given that the integral of  from 0 to 1 is 1/2, the identity
from 0 to 1 is 1/2, the identity  allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required. Defining
allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required. Defining

one has that

The definite integral is given by:

A more general expression can be obtained by defining

which, combined with the series representation, gives

Note that

This integral is also self-similar on the unit interval, under an action of the dyadic monoid described in the section Self similarity. Here, the representation is 4-dimensional, having the basis  . The action of g on the unit interval is the commuting diagram
. The action of g on the unit interval is the commuting diagram
=I_{w}\left(g\cdot x\right)=I_{w}\left({\frac {x}{2))\right)={\frac {x^{2)){8))+{\frac {w}{2))I_{w}(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b4166fbddbfd1c3d3c2b076e835b0a8d2b5159)
From this, one can then immediately read off the generators of the four-dimensional representation:

and

Repeated integrals transform under a 5,6,... dimensional representation.
Relation to simplicial complexes
Let

Define the Kruskal–Katona function

The Kruskal–Katona theorem states that this is the minimum number of (t − 1)-simplexes that are faces of a set of N t-simplexes.
As t and N approach infinity,
 (suitably normalized) approaches the blancmange curve.
(suitably normalized) approaches the blancmange curve.














































![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)














=T_{w}\left(g\cdot x\right)=T_{w}\left({\frac {x}{2))\right)={\frac {x}{2))+wT_{w}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80f034a1c5a31e0450f85eeddfb63b70991e300f)
=T_{w}(r\cdot x)=T_{w}(1-x)=T_{w}(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288657b954a7fa30be7fc8ce85bfb6e11c5da16b)









![{\displaystyle [m/2^{p},n/2^{p}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2acb3583829325eec7ea50efa165a45b3385898)
=a+bx+cT_{w}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/932dcafe233d050f126f04a32d13dee690b55c6d)











=I_{w}\left(g\cdot x\right)=I_{w}\left({\frac {x}{2))\right)={\frac {x^{2)){8))+{\frac {w}{2))I_{w}(x).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b4166fbddbfd1c3d3c2b076e835b0a8d2b5159)




