Hamid Naderi Yeganeh | |
|---|---|
 Naderi Yeganeh and a digital print of his artwork A Bird in Flight | |
| Born | July 26, 1990 |
| Nationality | Iranian |
| Alma mater | Sharif University of Technology (M.Sc.) University of Qom (B.Sc.) |
| Known for | mathematical art |
| Awards | |
Hamid Naderi Yeganeh (Persian: حمید نادری یگانه; born July 26, 1990, in Iran[1]) is an Iranian mathematical artist and digital artist.[2][3][4] He is known for using mathematical formulas to create drawings of real-life objects, intricate and symmetrical illustrations, animations, fractals and tessellations.[5][6][7][8][9] Naderi Yeganeh uses mathematics as the main tool to create artworks.[10] Therefore, his artworks can be totally described by mathematical concepts.[11][2] Mathematical concepts he uses in his work include trigonometric functions, exponential function, Fibonacci sequence, sawtooth wave, etc.[12][13][14][15][16]
His artwork 9,000 Ellipses was used as the background cover image of The American Mathematical Monthly – November 2017.[17][18][19][20] His artwork Heart was used as the image for the February page of the 2016 Calendar of Mathematical Imagery published by the American Mathematical Society.[21][22] His artwork Bird was used as the postcard image of the Art ∩ Math exhibit held at Center on Contemporary Art, Seattle in 2018.[23][24][25] One of Naderi Yeganeh's artworks was used as the cover image for Newsletter of Iranian Mathematical Society, Autumn 2015.[26] His works, including A Bird in Flight and Boat, have been used on several pages of the International Mathematical Knowledge Trust (IMKT)'s website.[27][28][29] His artwork A Bird in Flight was used on every page of the first volume of STATure, a publication of the Life Sciences Program at McMaster University.[5]
Naderi Yeganeh received his bachelor's degree in mathematics from the University of Qom[30] and a M.Sc. in pure mathematics from Sharif University of Technology.[31][32][30] His MSc thesis was focused on numerical methods for approximation and visualization of invariant manifolds in dynamical systems.[33] He won a gold medal at the 38th Iranian Mathematical Society’s nationwide mathematics competition held at Graduate University of Advanced Technology in May 2014 and a silver medal at the 39th IMS’s nationwide mathematics competition held at Yazd University in May 2015.[34][35][36][37] A special report about University of Qom's achievements and statistics in the years between 2013 and 2020 issued by the university's budget management and published by the Iranian MSRT stated Naderi Yeganeh's winning a gold medal at the 38th IMS’s math competition as one of the five outstanding achievements of the university's students in the 2013-2020 period.[38] According to one of the 38th IMS competition committee members, winning a gold medal by a student from University of Qom was a highlight of that competition.[39]
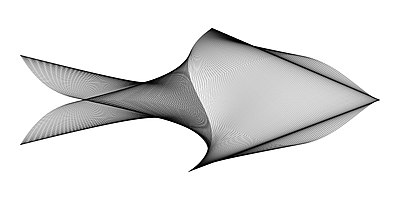
Naderi Yeganeh has introduced two methods to draw real-life objects with mathematical formulas.[4] By the first method, he creates tens of thousands of computer-generated mathematical figures to find a few interesting shapes accidentally. Then he changes the equations a little bit in order to increase the resemblance of the accidentally found shapes to real life objects.[40][41][42] For example, by using this method, he found some shapes that resemble birds, fishes and sailing boats.[43][44][45][46] In the second method, he draws a real life object with a step-by-step process. In each step, he tries to find out which mathematical formulas will produce the drawing.[47][4] For example, by using this method, he drew birds in flight, butterflies, human faces and plants using trigonometric functions.[48][49][50][47][51][52] Naderi Yeganeh says: "In order to create such shapes, it is very useful to know the properties of the trigonometric functions".[53][48] In 2018, in an interview with the Sharif University of Technology Public Relations Naderi Yeganeh said: I use mathematical concepts in a work of art in a way that it could be thoroughly explained in a paragraph. That makes the understanding of an artwork's scientific underpinning easier.[54]


An instance of drawing real things by using Yeganeh's methods is A Bird in Flight, which is the name of a number of bird-like geometric shapes introduced by Naderi Yeganeh. Yeganeh created those drawings by using the two methods mentioned above. An example of A Bird in Flight that was created by his first method is made of 500 segments defined in a Cartesian plane where for each the endpoints of the -th line segment are:
and
The 500 line segments defined above together form a shape in the Cartesian plane that resembles a flying bird. Looking at the line segments on the wings of the bird causes an optical illusion and may trick the viewer into thinking that the line segments are curved lines. Therefore, the shape can also be considered as an optical artwork.[49][8][13][55][52][56] Another version of A Bird in Flight that was designed by Naderi Yeganeh's second method is the union of all of the circles with center and radius , where , and
The set of the 20,001 circles defined above form a subset of the Cartesian plane that resembles a flying bird. Although this version's equations are a lot more complicated than the version made of 500 segments, it has a far better resemblance to a real flying bird.[49] It uses the periodic nature of trigonometric functions to form the feathers.[citation needed] Other works similar to this version of A Bird in Flight that was released by Naderi Yeganeh in 2016 are in the form of a flying parrot, magpie and stork.[48][57]
Naderi Yeganeh has designed some fractals and tessellations inspired by the continents.[58][59] For example, in 2015, he described the fractal Africa with an Africa-like octagon and its lateral inversion.[43][14][60][26] And he has created tessellations with Northern America-like and South America-like polygons.[61]

Fractal Africa is a fractal made of an infinite number of Africa-like octagons which was introduced by Naderi Yeganeh.[43][62][63] The fractal's octagons are similar to each other and they have some resemblance to the map of Africa.[8][64] The numbers of octagons of different sizes in the fractal is related to the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, 34, .... The height of the biggest octagon of the fractal is φ times larger than the height of second octagon; where φ is the well-known golden ratio.[14][13][65]
In 2015, CNN used the question "Is this the next da Vinci?" for the title of a video about Naderi Yeganeh's work and CNN Arabic used the title "Is this Iranian student da Vinci's successor?" for an article about him.[69][70][71] In 2015, Asia Society Philippines stated in a post on Facebook that "Hamid Naderi Yeganeh reveals the beauty of Math through Art".[72][73] In 2015, The National Museum of Mathematics stated in a post on Facebook that "Hamid Naderi Yeganeh takes graphing art to the next level!"[74] In 2016, Institute for Mathematics and its Applications commented on the Naderi Yeganeh's blog post showing how to draw human faces with mathematical equations: "Another reason that math wins".[75] In 2016, COSMOS raised this question in the introduction to its interview with Hamid Naderi Yeganeh: "Why couldn't high school mathematics be more like this?" in order to get its readers thinking about the potential of using Naderi Yeganeh's work in mathematics education.[76][4] In 2016, Mathematics in Education and Industry stated in a tweet that: "Hamid Naderi Yeganeh is a mathematical artist who's created plant images by trigonometric functions."[77] In 2016, Barbour Design Inc. stated on its own blog that "These often delicately intricate works are quite remarkable, and more astounding is that Yeganeh writes computer programs based on mathematical equations to produce them."[78] In 2017, Mathematical Association of America commented about one of Naderi Yeganeh's animations in a tweet: "Watch the beauty of trigonometric functions come alive".[79] In 2017, Fields Institute described Naderi Yeganeh's work as "beautiful math" in a tweet.[80] In 2017, Berkeley Lab commented on one of Naderi Yeganeh's blog posts: "Create stunning symmetrical images armed with a few equations and a computer".[81]
Naderi Yeganeh believes that there are an infinite number of ways of using mathematical tools in art.[82] In 2015, in an interview with CNN Style he said: "The power of mathematics is unlimited. There's an infinite number of great artworks that we can create".[8][83] He says, "I don’t think computer-made art clashes with human creativity, but it can change the role of artists.”[2] In 2016, He said in an interview with Dong-A Science: "For me, mathematics is the best tool to create works of art."[84] Hamid Naderi Yeganeh believes that introducing mathematical objects that resemble real recognizable things may encourage young people to pursue mathematics.[85] He believes mathematics is an international culture and mathematics can help to promote peace and love between nations.[86] Naderi Yeganeh believes that Pi is an international number and it can be a symbol of peace between nations.[61]
Below are some examples of Yeganeh's mathematical figures:[49]
 |
 |
 |
 |
 |