String art or pin and thread art, is characterized by an arrangement of colored thread strung between points to form geometric patterns or representational designs such as a ship's sails, sometimes with other artist material comprising the remainder of the work. Thread, wire, or string is wound around a grid of nails hammered into a velvet-covered wooden board. Though straight lines are formed by the string, the slightly different angles and metric positions at which strings intersect gives the appearance of Bézier curves (as in the mathematical concept of envelope of a family of straight lines). Quadratic Bézier curve are obtained from strings based on two intersecting segments. Other forms of string art include Spirelli, which is used for cardmaking and scrapbooking, and curve stitching, in which string is stitched through holes.
String art has its origins in the 'curve stitch' activities invented by Mary Everest Boole at the end of the 19th century to make mathematical ideas more accessible to children.[1] It was popularised as a decorative craft in the late 1960s through kits and books.[2]
A computational form of string art that can produce photo-realistic artwork was introduced by Petros Vrellis, in 2016. [3]
Gallery
[edit]-
String art star design
-
Computational String art by Petros Vrellis (2016)
-
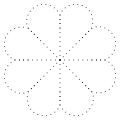
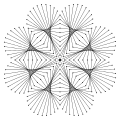
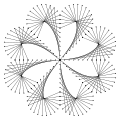
Stringart: Flower hole pattern
-
Stringart: Flower filled sewing pattern
-
Stringart: Flower loop sewing pattern
-
Stringart: Flower half-loop sewing pattern
See also
[edit]References
[edit]- ^ Michalowicz, Karen Dee Ann (1996). "Mary Everest Boole: An Erstwhile Pedagogist for Contemporary Times". In Calinger, Ronald (ed.). Vita mathematica. Cambridge: Cambridge University Press. p. 291. ISBN 0-88385-097-4.
- ^ Blanken, Rain, author. (2018-06-15). String art magic : the secrets to crafting geometric art with string and nail. ISBN 978-1-940611-73-0. OCLC 988301633.
((cite book)):|last=has generic name (help)CS1 maint: multiple names: authors list (link) - ^ Bown, Oliver (2021). "Beyond the Creative Species: Making Machines That Make Art and Music". The MIT Press. ISBN 9780262045018.
Bibliography
[edit]- Lois Kreischer (1971). Symmography. Crown Publishers, New York, NY. ISBN 0-517-50274-7
- Robert Sharpton (1972). Designing In String. Cunningham Art Products, Inc. No ISBN.
- Mark Jansen, Ric Barline, Fred Fortune (1972). The Art of Geometric Thread Design. Open Door Company, Campbell, CA. No ISBN.
- Brian and Patricia Eales (1973). Pin and Thread. Flarepath Printers Ltd., Great Britain. No ISBN.
- Glen D. Saeger (1973). String Things You Can Make. Sterling Publishing Co., New York, NY. ISBN 0-8069-5262-8
- Glen D. Saeger (1973). String Designs. Sterling Publishing Co., New York, NY. ISBN 0-8069-5320-9
- Vivian Bowler (1974). 44 String and Nail Art Projects. Crown Publishers, New York, NY. No ISBN.
- James E. Gick (1974). Thread Design. Hazel Pearson Crafts, Rosemead, CA. No ISBN.
- Douglas K. Dix (1975). Filography. Pan Books Ltd., London. ISBN 0-330-24155-9
- Robert Sharpton (1975). String Art: Step-By-Step. Chilton Book Co. Radnor, PA. ISBN 0-8019-6131-9
- Marie-Claude Riviere (1975). Pin Pictures With Wire and Thread. Sterling Publishing Co., New York, NY. ISBN ?
- Fran Risting (1975). String Art. Drake Publishing, NY and London. ISBN 0-87749-816-4
- Unknown Author (1975). String Art Made Easy. Clapper Publications Co. Ridge Park, Illinois. No ISBN.
- Compilation (1976). String Art Encyclopedia. Sterling Publishing Co., New York, NY. ISBN 0-8069-5362-4
- Richard Ohanian (1976). The Family Creative Workshop. Plenary Publications International, New York, NY. ISBN 0-88459-017-8
- Warren Farnworth (1977). Techniques and Designs in Pin and Thread Craft. BT Batsford Ltd., London. ISBN 0-7134-0535-X
- Roland and Dominique Cauro (1978). Stringcraft. Sterling Publishing Co., New York, NY. ISBN 0-8069-5364-0
- Raymond Gautard (1978). The Beautiful String Art Book. Sterling Publishing Co., New York, NY. ISBN 0-8069-5386-1
- Jon Millington (1989). 'Curve Stitching'. Tarquin Publications, London, UK ISBN 0-9062-1265-0
- Jane Hermsen (2003). Spirelli. Forte Publishers BV, The Netherlands. ISBN 90-5877-271-3
- Ali Gökçe Yılmaz (2013). "Futursuz Futurist String Art". Istanbul. No ISBN
- Rain Blanken (2018) "String Art Magic: Secrets to Crafting Geometric Art with String and Nail" ISBN 978-1-940611-73-0
External links
[edit]| Textile | |
|---|---|
| Paper | |
| Wood | |
| Ceramic | |
| Glass | |
| Metal | |
| Other |
|