Archimedes of Syracuse | |
|---|---|
Ἀρχιμήδης | |
 Archimedes Thoughtful by Domenico Fetti (1620) | |
| Born | c. 287 BC |
| Died | c. 212 BC (aged approximately 75) Syracuse, Sicily |
| Known for | |
| Scientific career | |
| Fields | Mathematics Physics Astronomy Mechanics Engineering |
Archimedes of Syracuse[a] (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez;[2] c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily.[3] Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,[4] Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems.[5][6] These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.[7][8]
Archimedes' other mathematical achievements include deriving an approximation of pi, defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever,[9] the widespread use of the concept of center of gravity,[10] and the enunciation of the law of buoyancy known as Archimedes' principle.[11] He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion.
Archimedes died during the siege of Syracuse, when he was killed by a Roman soldier despite orders that he should not be harmed. Cicero describes visiting Archimedes' tomb, which was surmounted by a sphere and a cylinder that Archimedes requested be placed there to represent his mathematical discoveries.
Unlike his inventions, Archimedes' mathematical writings were little known in antiquity. Mathematicians from Alexandria read and quoted him, but the first comprehensive compilation was not made until c. 530 AD by Isidore of Miletus in Byzantine Constantinople, while commentaries on the works of Archimedes by Eutocius in the 6th century opened them to wider readership for the first time. The relatively few copies of Archimedes' written work that survived through the Middle Ages were an influential source of ideas for scientists during the Renaissance and again in the 17th century,[12][13] while the discovery in 1906 of previously lost works by Archimedes in the Archimedes Palimpsest has provided new insights into how he obtained mathematical results.[14][15][16][17]

Archimedes was born c. 287 BC in the seaport city of Syracuse, Sicily, at that time a self-governing colony in Magna Graecia. The date of birth is based on a statement by the Byzantine Greek scholar John Tzetzes that Archimedes lived for 75 years before his death in 212 BC.[8] In the Sand-Reckoner, Archimedes gives his father's name as Phidias, an astronomer about whom nothing else is known.[18][19] A biography of Archimedes was written by his friend Heracleides, but this work has been lost, leaving the details of his life obscure. It is unknown, for instance, whether he ever married or had children, or if he ever visited Alexandria, Egypt, during his youth.[20] From his surviving written works, it is clear that he maintained collegial relations with scholars based there, including his friend Conon of Samos and the head librarian Eratosthenes of Cyrene.[b]
The standard versions of Archimedes' life were written long after his death by Greek and Roman historians. The earliest reference to Archimedes occurs in The Histories by Polybius (c. 200–118 BC), written about 70 years after his death.[19] It sheds little light on Archimedes as a person, and focuses on the war machines that he is said to have built in order to defend the city from the Romans.[21] Polybius remarks how, during the Second Punic War, Syracuse switched allegiances from Rome to Carthage, resulting in a military campaign under the command of Marcus Claudius Marcellus and Appius Claudius Pulcher, who besieged the city from 213 to 212 BC. He notes that the Romans underestimated Syracuse's defenses, and mentions several machines Archimedes designed, including improved catapults, crane-like machines that could be swung around in an arc, and other stone-throwers. Although the Romans ultimately captured the city, they suffered considerable losses due to Archimedes' inventiveness.[22]
Cicero (106–43 BC) mentions Archimedes in some of his works.[19] While serving as a quaestor in Sicily, Cicero found what was presumed to be Archimedes' tomb near the Agrigentine gate in Syracuse, in a neglected condition and overgrown with bushes.[8][23] Cicero had the tomb cleaned up and was able to see the carving and read some of the verses that had been added as an inscription. The tomb carried a sculpture illustrating Archimedes' favorite mathematical proof, that the volume and surface area of the sphere are two-thirds that of an enclosing cylinder including its bases.[24][25] He also mentions that Marcellus brought to Rome two planetariums Archimedes built.[26] The Roman historian Livy (59 BC–17 AD) retells Polybius' story of the capture of Syracuse and Archimedes' role in it.[21]

Plutarch (45–119 AD) wrote in his Parallel Lives that Archimedes was related to King Hiero II, the ruler of Syracuse,[28][19] although Cicero suggests he was of humble origin..[19] Plutarch also provides at least two accounts on how Archimedes died after the city was taken.[19] According to the most popular account, Archimedes was contemplating a mathematical diagram when the city was captured. A Roman soldier commanded him to come and meet Marcellus, but he declined, saying that he had to finish working on the problem. This enraged the soldier, who killed Archimedes with his sword. Another story has Archimedes carrying mathematical instruments before being killed because a soldier thought they were valuable items. Marcellus was reportedly angered by Archimedes' death, as he considered him a valuable scientific asset (he called Archimedes "a geometrical Briareus") and had ordered that he should not be harmed.[29][30]
The last words attributed to Archimedes are "Do not disturb my circles" (Latin, "Noli turbare circulos meos"; Katharevousa Greek, "μὴ μου τοὺς κύκλους τάραττε"), a reference to the mathematical drawing that he was supposedly studying when disturbed by the Roman soldier..[19] There is no reliable evidence that Archimedes uttered these words and they do not appear in Plutarch's account. A similar quotation is found in the work of Valerius Maximus (fl. 30 AD), who wrote in Memorable Doings and Sayings, "... sed protecto manibus puluere 'noli' inquit, 'obsecro, istum disturbare'" ("... but protecting the dust with his hands, said 'I beg of you, do not disturb this'").[21]
|
Main article: Archimedes' principle |

The most widely known anecdote about Archimedes tells of how he invented a method for determining the volume of an object with an irregular shape. According to Vitruvius, a crown for a temple had been made for King Hiero II of Syracuse, who supplied the pure gold to be used. The crown was likely made in the shape of a votive wreath.[31] Archimedes was asked to determine whether some silver had been substituted by the goldsmith without damaging the crown, so he could not melt it down into a regularly shaped body in order to calculate its density.[32]
In this account, Archimedes noticed while taking a bath that the level of the water in the tub rose as he got in, and realized that this effect could be used to determine the golden crown's volume. Archimedes was so excited by this discovery that he took to the streets naked, having forgotten to dress, crying "Eureka!" (Greek: "εὕρηκα, heúrēka!, lit. 'I have found [it]!'). For practical purposes water is incompressible,[33] so the submerged crown would displace an amount of water equal to its own volume. By dividing the mass of the crown by the volume of water displaced, its density could be obtained; if cheaper and less dense metals had been added, the density would be lower than that of gold. Archimedes found that this is what had happened, proving that silver had been mixed in.[31][32]
The story of the golden crown does not appear anywhere in Archimedes' known works. The practicality of the method described has been called into question due to the extreme accuracy that would be required to measure water displacement.[34] Archimedes may have instead sought a solution that applied the hydrostatics principle known as Archimedes' principle, found in his treatise On Floating Bodies: a body immersed in a fluid experiences a buoyant force equal to the weight of the fluid it displaces.[35] Using this principle, it would have been possible to compare the density of the crown to that of pure gold by balancing it on a scale with a pure gold reference sample of the same weight, then immersing the apparatus in water. The difference in density between the two samples would cause the scale to tip accordingly.[11] Galileo Galilei, who invented a hydrostatic balance in 1586 inspired by Archimedes' work, considered it "probable that this method is the same that Archimedes followed, since, besides being very accurate, it is based on demonstrations found by Archimedes himself."[36][37]
While Archimedes did not invent the lever, he gave a mathematical proof of the principle involved in his work On the Equilibrium of Planes.[38] Earlier descriptions of the principle of the lever are found in a work by Euclid and in the Mechanical Problems, belonging to the Peripatetic school of the followers of Aristotle, the authorship of which has been attributed by some to Archytas.[39][40]
There are several, often conflicting, reports regarding Archimedes' feats using the lever to lift very heavy objects. Plutarch describes how Archimedes designed block-and-tackle pulley systems, allowing sailors to use the principle of leverage to lift objects that would otherwise have been too heavy to move.[41] According to Pappus of Alexandria, Archimedes' work on levers and his understanding of mechanical advantage caused him to remark: "Give me a place to stand on, and I will move the Earth" (Greek: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω).[42] Olympiodorus later attributed the same boast to Archimedes' invention of the baroulkos, a kind of windlass, rather than the lever.[43]
|
Main article: Archimedes' screw |

A large part of Archimedes' work in engineering probably arose from fulfilling the needs of his home city of Syracuse. Athenaeus of Naucratis quotes a certain Moschion in a description on how King Hiero II commissioned the design of a huge ship, the Syracusia, which could be used for luxury travel, carrying supplies, and as a display of naval power.[44] The Syracusia is said to have been the largest ship built in classical antiquity and, according to Moschion's account, it was launched by Archimedes.[43] The ship presumably was capable of carrying 600 people and included garden decorations, a gymnasium, and a temple dedicated to the goddess Aphrodite among its facilities.[45] The account also mentions that, in order to remove any potential water leaking through the hull, a device with a revolving screw-shaped blade inside a cylinder was designed by Archimedes.
Archimedes' screw was turned by hand, and could also be used to transfer water from a low-lying body of water into irrigation canals. The screw is still in use today for pumping liquids and granulated solids such as coal and grain. Described by Vitruvius, Archimedes' device may have been an improvement on a screw pump that was used to irrigate the Hanging Gardens of Babylon.[46][47] The world's first seagoing steamship with a screw propeller was the SS Archimedes, which was launched in 1839 and named in honor of Archimedes and his work on the screw.[48]
Archimedes is said to have designed a claw as a weapon to defend the city of Syracuse. Also known as "the ship shaker", the claw consisted of a crane-like arm from which a large metal grappling hook was suspended. When the claw was dropped onto an attacking ship the arm would swing upwards, lifting the ship out of the water and possibly sinking it.[49]
There have been modern experiments to test the feasibility of the claw, and in 2005 a television documentary entitled Superweapons of the Ancient World built a version of the claw and concluded that it was a workable device.[50] Archimedes has also been credited with improving the power and accuracy of the catapult, and with inventing the odometer during the First Punic War. The odometer was described as a cart with a gear mechanism that dropped a ball into a container after each mile traveled.[51]
|
Main article: Archimedes' heat ray |

Archimedes is believed to have used mirrors acting collectively as a parabolic reflector to burn ships attacking Syracuse. Although he may have written a work on mirrors entitled Catoptrica,[c] his contemporary Diocles made no mention of Archimedes or burning ships in his treatise about focusing reflectors. In the second century AD, Lucian wrote that during the siege of Syracuse Archimedes burned enemy ships. Nearly four hundred years later, Anthemius, despite skepticism, tried to reconstruct Archimedes' hypothetical reflector geometry.[52]
Often called the "Archimedes heat ray", the purported mirror arrangement focused sunlight onto approaching ships, presumably causing them to catch fire, similar to a heliostat or solar furnace.[53] Archimedes' alleged heat ray has been the subject of an ongoing debate about its credibility since the Renaissance.[54] René Descartes rejected it as false, while modern researchers have attempted to recreate the effect using only the means that would have been available to Archimedes, mostly with negative results.[55][56] It has been suggested that a large array of highly polished bronze or copper shields acting as mirrors could have been employed to focus sunlight onto a ship, but the overall effect would have been blinding, dazzling, or distracting the crew of the ship rather than fire.[57]
Archimedes discusses astronomical measurements of the Earth, Sun, and Moon, as well as Aristarchus' heliocentric model of the universe, in the Sand-Reckoner. Without the use of either trigonometry or a table of chords, Archimedes determines the Sun's apparent diameter by first describing the procedure and instrument used to make observations (a straight rod with pegs or grooves),[58][59] applying correction factors to these measurements, and finally giving the result in the form of upper and lower bounds to account for observational error.[18] Ptolemy, quoting Hipparchus, also references Archimedes' solstice observations in the Almagest. This would make Archimedes the first known Greek to have recorded multiple solstice dates and times in successive years.[20]
Cicero's De re publica portrays a fictional conversation taking place in 129 BC. After the capture of Syracuse in the Second Punic War, Marcellus is said to have taken back to Rome two mechanisms which were constructed by Archimedes and which showed the motion of the Sun, Moon and five planets. Cicero also mentions similar mechanisms designed by Thales of Miletus and Eudoxus of Cnidus. The dialogue says that Marcellus kept one of the devices as his only personal loot from Syracuse, and donated the other to the Temple of Virtue in Rome. Marcellus' mechanism was demonstrated, according to Cicero, by Gaius Sulpicius Gallus to Lucius Furius Philus, who described it thus:[60][61]
Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione.
When Gallus moved the globe, it happened that the Moon followed the Sun by as many turns on that bronze contrivance as in the sky itself, from which also in the sky the Sun's globe became to have that same eclipse, and the Moon came then to that position which was its shadow on the Earth when the Sun was in line.
This is a description of a small planetarium. Pappus of Alexandria reports on a now lost treatise by Archimedes dealing with the construction of these mechanisms entitled On Sphere-Making.[26][62] Modern research in this area has been focused on the Antikythera mechanism, another device built c. 100 BC probably designed with a similar purpose.[63] Constructing mechanisms of this kind would have required a sophisticated knowledge of differential gearing.[64] This was once thought to have been beyond the range of the technology available in ancient times, but the discovery of the Antikythera mechanism in 1902 has confirmed that devices of this kind were known to the ancient Greeks.[65][66]
While he is often regarded as a designer of mechanical devices, Archimedes also made contributions to the field of mathematics. Plutarch wrote that Archimedes "placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life",[29] though some scholars believe this may be a mischaracterization.[67][68][69]
Archimedes was able to use indivisibles (a precursor to infinitesimals) in a way that is similar to modern integral calculus.[5] Through proof by contradiction (reductio ad absurdum), he could give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay. This technique is known as the method of exhaustion, and he employed it to approximate the areas of figures and the value of π.
In Measurement of a Circle, he did this by drawing a larger regular hexagon outside a circle then a smaller regular hexagon inside the circle, and progressively doubling the number of sides of each regular polygon, calculating the length of a side of each polygon at each step. As the number of sides increases, it becomes a more accurate approximation of a circle. After four such steps, when the polygons had 96 sides each, he was able to determine that the value of π lay between 31/7 (approx. 3.1429) and 310/71 (approx. 3.1408), consistent with its actual value of approximately 3.1416.[70] He also proved that the area of a circle was equal to π multiplied by the square of the radius of the circle ().
In On the Sphere and Cylinder, Archimedes postulates that any magnitude when added to itself enough times will exceed any given magnitude. Today this is known as the Archimedean property of real numbers.[71]
Archimedes gives the value of the square root of 3 as lying between 265/153 (approximately 1.7320261) and 1351/780 (approximately 1.7320512) in Measurement of a Circle. The actual value is approximately 1.7320508, making this a very accurate estimate. He introduced this result without offering any explanation of how he had obtained it. This aspect of the work of Archimedes caused John Wallis to remark that he was: "as it were of set purpose to have covered up the traces of his investigation as if he had grudged posterity the secret of his method of inquiry while he wished to extort from them assent to his results."[72] It is possible that he used an iterative procedure to calculate these values.[73][74]

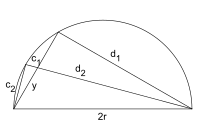
In Quadrature of the Parabola, Archimedes proved that the area enclosed by a parabola and a straight line is 4/3 times the area of a corresponding inscribed triangle as shown in the figure at right. He expressed the solution to the problem as an infinite geometric series with the common ratio 1/4:
If the first term in this series is the area of the triangle, then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines, and whose third vertex is where the line that is parallel to the parabola's axis and that passes through the midpoint of the base intersects the parabola, and so on. This proof uses a variation of the series 1/4 + 1/16 + 1/64 + 1/256 + · · · which sums to 1/3.
In The Sand Reckoner, Archimedes set out to calculate a number that was greater than the grains of sand needed to fill the universe. In doing so, he challenged the notion that the number of grains of sand was too large to be counted. He wrote:
There are some, King Gelo, who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited.
To solve the problem, Archimedes devised a system of counting based on the myriad. The word itself derives from the Greek μυριάς, murias, for the number 10,000. He proposed a number system using powers of a myriad of myriads (100 million, i.e., 10,000 x 10,000) and concluded that the number of grains of sand required to fill the universe would be 8 vigintillion, or 8×1063.[75]

The works of Archimedes were written in Doric Greek, the dialect of ancient Syracuse.[76] Many written works by Archimedes have not survived or are only extant in heavily edited fragments; at least seven of his treatises are known to have existed due to references made by other authors.[8] Pappus of Alexandria mentions On Sphere-Making and another work on polyhedra, while Theon of Alexandria quotes a remark about refraction from the now-lost Catoptrica.[c]
Archimedes made his work known through correspondence with the mathematicians in Alexandria. The writings of Archimedes were first collected by the Byzantine Greek architect Isidore of Miletus (c. 530 AD), while commentaries on the works of Archimedes written by Eutocius in the sixth century AD helped to bring his work a wider audience. Archimedes' work was translated into Arabic by Thābit ibn Qurra (836–901 AD), and into Latin via Arabic by Gerard of Cremona (c. 1114–1187). Direct Greek to Latin translations were later done by William of Moerbeke (c. 1215–1286) and Iacobus Cremonensis (c. 1400–1453).[77][78]
During the Renaissance, the Editio princeps (First Edition) was published in Basel in 1544 by Johann Herwagen with the works of Archimedes in Greek and Latin.[79]
The following are ordered chronologically based on new terminological and historical criteria set by Knorr (1978) and Sato (1986).[80][81]
|
Main article: Measurement of a Circle |
This is a short work consisting of three propositions. It is written in the form of a correspondence with Dositheus of Pelusium, who was a student of Conon of Samos. In Proposition II, Archimedes gives an approximation of the value of pi (π), showing that it is greater than 223/71 (3.1408...) and less than 22/7 (3.1428...).
|
Main article: The Sand Reckoner |
In this treatise, also known as Psammites, Archimedes finds a number that is greater than the grains of sand needed to fill the universe. This book mentions the heliocentric theory of the solar system proposed by Aristarchus of Samos, as well as contemporary ideas about the size of the Earth and the distance between various celestial bodies. By using a system of numbers based on powers of the myriad, Archimedes concludes that the number of grains of sand required to fill the universe is 8×1063 in modern notation. The introductory letter states that Archimedes' father was an astronomer named Phidias. The Sand Reckoner is the only surviving work in which Archimedes discusses his views on astronomy.[82]
|
Main article: On the Equilibrium of Planes |
There are two books to On the Equilibrium of Planes: the first contains seven postulates and fifteen propositions, while the second book contains ten propositions. In the first book, Archimedes proves the law of the lever, which states that:
Magnitudes are in equilibrium at distances reciprocally proportional to their weights.
Archimedes uses the principles derived to calculate the areas and centers of gravity of various geometric figures including triangles, parallelograms and parabolas.[83]
|
Main article: Quadrature of the Parabola |
In this work of 24 propositions addressed to Dositheus, Archimedes proves by two methods that the area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height. He achieves this in one of his proofs by calculating the value of a geometric series that sums to infinity with the ratio 1/4.
|
Main article: On the Sphere and Cylinder |

In this two-volume treatise addressed to Dositheus, Archimedes obtains the result of which he was most proud, namely the relationship between a sphere and a circumscribed cylinder of the same height and diameter. The volume is 4/3πr3 for the sphere, and 2πr3 for the cylinder. The surface area is 4πr2 for the sphere, and 6πr2 for the cylinder (including its two bases), where r is the radius of the sphere and cylinder.
|
Main article: On Spirals |
This work of 28 propositions is also addressed to Dositheus. The treatise defines what is now called the Archimedean spiral. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity. Equivalently, in modern polar coordinates (r, θ), it can be described by the equation with real numbers a and b.
This is an early example of a mechanical curve (a curve traced by a moving point) considered by a Greek mathematician.
|
Main article: On Conoids and Spheroids |
This is a work in 32 propositions addressed to Dositheus. In this treatise Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids.
|
Main article: On Floating Bodies |
There are two books of On Floating Bodies. In the first book, Archimedes spells out the law of equilibrium of fluids and proves that water will adopt a spherical form around a center of gravity. This may have been an attempt at explaining the theory of contemporary Greek astronomers such as Eratosthenes that the Earth is round. The fluids described by Archimedes are not self-gravitating since he assumes the existence of a point towards which all things fall in order to derive the spherical shape. Archimedes' principle of buoyancy is given in this work, stated as follows:[11][84]
Any body wholly or partially immersed in fluid experiences an upthrust equal to, but opposite in direction to, the weight of the fluid displaced.
In the second part, he calculates the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, similar to the way that icebergs float.[85]
|
Main article: Ostomachion |

Also known as Loculus of Archimedes or Archimedes' Box,[86] this is a dissection puzzle similar to a Tangram, and the treatise describing it was found in more complete form in the Archimedes Palimpsest. Archimedes calculates the areas of the 14 pieces which can be assembled to form a square. Reviel Netz of Stanford University argued in 2003 that Archimedes was attempting to determine how many ways the pieces could be assembled into the shape of a square. Netz calculates that the pieces can be made into a square 17,152 ways.[87] The number of arrangements is 536 when solutions that are equivalent by rotation and reflection are excluded.[88] The puzzle represents an example of an early problem in combinatorics.
The origin of the puzzle's name is unclear, and it has been suggested that it is taken from the Ancient Greek word for "throat" or "gullet", stomachos (στόμαχος).[89] Ausonius calls the puzzle Ostomachion, a Greek compound word formed from the roots of osteon (ὀστέον, 'bone') and machē (μάχη, 'fight').[86]
|
Main article: Archimedes' cattle problem |
Gotthold Ephraim Lessing discovered this work in a Greek manuscript consisting of a 44-line poem in the Herzog August Library in Wolfenbüttel, Germany in 1773. It is addressed to Eratosthenes and the mathematicians in Alexandria. Archimedes challenges them to count the numbers of cattle in the Herd of the Sun by solving a number of simultaneous Diophantine equations. There is a more difficult version of the problem in which some of the answers are required to be square numbers. A. Amthor first solved this version of the problem[90] in 1880, and the answer is a very large number, approximately 7.760271×10206544.[91]
|
Main article: The Method of Mechanical Theorems |
This treatise was thought lost until the discovery of the Archimedes Palimpsest in 1906. In this work Archimedes uses indivisibles,[5][6] and shows how breaking up a figure into an infinite number of infinitely small parts can be used to determine its area or volume. He may have considered this method lacking in formal rigor, so he also used the method of exhaustion to derive the results. As with The Cattle Problem, The Method of Mechanical Theorems was written in the form of a letter to Eratosthenes in Alexandria.
Archimedes' Book of Lemmas or Liber Assumptorum is a treatise with 15 propositions on the nature of circles. The earliest known copy of the text is in Arabic. T. L. Heath and Marshall Clagett argued that it cannot have been written by Archimedes in its current form, since it quotes Archimedes, suggesting modification by another author. The Lemmas may be based on an earlier work by Archimedes that is now lost.[92]
It has also been claimed that the formula for calculating the area of a triangle from the length of its sides was known to Archimedes,[d] though its first appearance is in the work of Heron of Alexandria in the 1st century AD.[93] Other questionable attributions to Archimedes' work include the Latin poem Carmen de ponderibus et mensuris (4th or 5th century), which describes the use of a hydrostatic balance, to solve the problem of the crown, and the 12th-century text Mappae clavicula, which contains instructions on how to perform assaying of metals by calculating their specific gravities.[94][95]
|
Main article: Archimedes Palimpsest |

The foremost document containing Archimedes' work is the Archimedes Palimpsest. In 1906, the Danish professor Johan Ludvig Heiberg visited Constantinople to examine a 174-page goatskin parchment of prayers, written in the 13th century, after reading a short transcription published seven years earlier by Papadopoulos-Kerameus.[96][97] He confirmed that it was indeed a palimpsest, a document with text that had been written over an erased older work. Palimpsests were created by scraping the ink from existing works and reusing them, a common practice in the Middle Ages, as vellum was expensive. The older works in the palimpsest were identified by scholars as 10th-century copies of previously lost treatises by Archimedes.[96][98] The parchment spent hundreds of years in a monastery library in Constantinople before being sold to a private collector in the 1920s. On 29 October 1998, it was sold at auction to an anonymous buyer for a total of $2.2 million.[99][100]
The palimpsest holds seven treatises, including the only surviving copy of On Floating Bodies in the original Greek. It is the only known source of The Method of Mechanical Theorems, referred to by Suidas and thought to have been lost forever. Stomachion was also discovered in the palimpsest, with a more complete analysis of the puzzle than had been found in previous texts. The palimpsest was stored at the Walters Art Museum in Baltimore, Maryland, where it was subjected to a range of modern tests including the use of ultraviolet and X-ray light to read the overwritten text.[101] It has since returned to its anonymous owner.[102][103]
The treatises in the Archimedes Palimpsest include:
|
Further information: List of things named after Archimedes and Eureka |
Sometimes called the father of mathematics and mathematical physics, Archimedes had a wide influence on mathematics and science.[104]

Historians of science and mathematics almost universally agree that Archimedes was the finest mathematician from antiquity. Eric Temple Bell, for instance, wrote:
Any list of the three “greatest” mathematicians of all history would include the name of Archimedes. The other two usually associated with him are Newton and Gauss. Some, considering the relative wealth—or poverty—of mathematics and physical science in the respective ages in which these giants lived, and estimating their achievements against the background of their times, would put Archimedes first.[105]
Likewise, Alfred North Whitehead and George F. Simmons said of Archimedes:
... in the year 1500 Europe knew less than Archimedes who died in the year 212 BC ...[106]
If we consider what all other men accomplished in mathematics and physics, on every continent and in every civilization, from the beginning of time down to the seventeenth century in Western Europe, the achievements of Archimedes outweighs it all. He was a great civilization all by himself.[107]
Reviel Netz, Suppes Professor in Greek Mathematics and Astronomy at Stanford University and an expert in Archimedes notes:
And so, since Archimedes led more than anyone else to the formation of the calculus and since he was the pioneer of the application of mathematics to the physical world, it turns out that Western science is but a series of footnotes to Archimedes. Thus, it turns out that Archimedes is the most important scientist who ever lived.[108]
Leonardo da Vinci repeatedly expressed admiration for Archimedes, and attributed his invention Architonnerre to Archimedes.[109][110][111] Galileo called him "superhuman" and "my master",[112][113] while Huygens said, "I think Archimedes is comparable to no one", consciously emulating him in his early work.[114] Leibniz said, "He who understands Archimedes and Apollonius will admire less the achievements of the foremost men of later times".[115] Gauss's heroes were Archimedes and Newton,[116] and Moritz Cantor, who studied under Gauss in the University of Göttingen, reported that he once remarked in conversation that "there had been only three epoch-making mathematicians: Archimedes, Newton, and Eisenstein".[117]
The inventor Nikola Tesla praised him, saying:
Archimedes was my ideal. I admired the works of artists, but to my mind, they were only shadows and semblances. The inventor, I thought, gives to the world creations which are palpable, which live and work.[118]

There is a crater on the Moon named Archimedes (29°42′N 4°00′W / 29.7°N 4.0°W) in his honor, as well as a lunar mountain range, the Montes Archimedes (25°18′N 4°36′W / 25.3°N 4.6°W).[119]
The Fields Medal for outstanding achievement in mathematics carries a portrait of Archimedes, along with a carving illustrating his proof on the sphere and the cylinder. The inscription around the head of Archimedes is a quote attributed to 1st century AD poet Manilius, which reads in Latin: Transire suum pectus mundoque potiri ("Rise above oneself and grasp the world").[120][121][122]
Archimedes has appeared on postage stamps issued by East Germany (1973), Greece (1983), Italy (1983), Nicaragua (1971), San Marino (1982), and Spain (1963).[123]
The exclamation of Eureka! attributed to Archimedes is the state motto of California. In this instance, the word refers to the discovery of gold near Sutter's Mill in 1848 which sparked the California Gold Rush.[124]