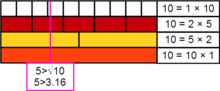
Demonstration, with Cuisenaire rods, that the number 10 is an unusual number, its largest prime factor being 5, which is greater than √10 ≈ 3.16

In number theory, an unusual number is a natural number n whose largest prime factor is strictly greater than ${\displaystyle {\sqrt {n))}$.

A k-smooth number has all its prime factors less than or equal to k, therefore, an unusual number is non-${\displaystyle {\sqrt {n))}$-smooth.

Relation to prime numbers

All prime numbers are unusual. For any prime p, its multiples less than p² are unusual, that is p, ... (p-1)p, which have a density 1/p in the interval (p, p²).

Examples

The first few unusual numbers are

2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 26, 28, 29, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 44, 46, 47, 51, 52, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67, ... (sequence A064052 in the OEIS)

The first few non-prime (composite) unusual numbers are

6, 10, 14, 15, 20, 21, 22, 26, 28, 33, 34, 35, 38, 39, 42, 44, 46, 51, 52, 55, 57, 58, 62, 65, 66, 68, 69, 74, 76, 77, 78, 82, 85, 86, 87, 88, 91, 92, 93, 94, 95, 99, 102, ... (sequence A063763 in the OEIS)

Distribution

If we denote the number of unusual numbers less than or equal to n by u(n) then u(n) behaves as follows:

Richard Schroeppel stated in 1972 that the asymptotic probability that a randomly chosen number is unusual is ln(2). In other words:

${\displaystyle \lim _{n\rightarrow \infty }{\frac {u(n)}{n))=\ln(2)=0.693147\dots \,.}$