Type of matrix in algebraic graph theory
In the mathematical field of algebraic graph theory, the degree matrix of an undirected graph is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex.[1] It is used together with the adjacency matrix to construct the Laplacian matrix of a graph: the Laplacian matrix is the difference of the degree matrix and the adjacency matrix.[2]
Example
The following undirected graph has a 6x6 degree matrix with values:
| Vertex labeled graph
|
Degree matrix
|
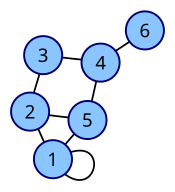
|

|
Note that in the case of undirected graphs, an edge that starts and ends in the same node increases the corresponding degree value by 2 (i.e. it is counted twice).
Properties
The degree matrix of a k-regular graph has a constant diagonal of  .
.
According to the degree sum formula, the trace of the degree matrix is twice the number of edges of the considered graph.









