| Statistics |
|---|
 |
| Part of a series on | ||
| Mathematics | ||
|---|---|---|
|
|
||
|
| ||


Statistics (from German: Statistik, orig. "description of a state, a country")[1][2] is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data.[3][4][5] In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.[6]
When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation.
Two main statistical methods are used in data analysis: descriptive statistics, which summarize data from a sample using indexes such as the mean or standard deviation, and inferential statistics, which draw conclusions from data that are subject to random variation (e.g., observational errors, sampling variation).[7] Descriptive statistics are most often concerned with two sets of properties of a distribution (sample or population): central tendency (or location) seeks to characterize the distribution's central or typical value, while dispersion (or variability) characterizes the extent to which members of the distribution depart from its center and each other. Inferences on mathematical statistics are made under the framework of probability theory, which deals with the analysis of random phenomena.
A standard statistical procedure involves the collection of data leading to a test of the relationship between two statistical data sets, or a data set and synthetic data drawn from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis of no relationship between two data sets. Rejecting or disproving the null hypothesis is done using statistical tests that quantify the sense in which the null can be proven false, given the data that are used in the test. Working from a null hypothesis, two basic forms of error are recognized: Type I errors (null hypothesis is rejected when it is in fact true, giving a "false positive") and Type II errors (null hypothesis fails to be rejected when an it is in fact false, giving a "false negative"). Multiple problems have come to be associated with this framework, ranging from obtaining a sufficient sample size to specifying an adequate null hypothesis.[7]
Statistical measurement processes are also prone to error in regards to the data that they generate. Many of these errors are classified as random (noise) or systematic (bias), but other types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also occur. The presence of missing data or censoring may result in biased estimates and specific techniques have been developed to address these problems.
Introduction
[edit]Statistics is a mathematical body of science that pertains to the collection, analysis, interpretation or explanation, and presentation of data,[8] or as a branch of mathematics.[9] Some consider statistics to be a distinct mathematical science rather than a branch of mathematics. While many scientific investigations make use of data, statistics is generally concerned with the use of data in the context of uncertainty and decision-making in the face of uncertainty.[10][11]
In applying statistics to a problem, it is common practice to start with a population or process to be studied. Populations can be diverse topics, such as "all people living in a country" or "every atom composing a crystal". Ideally, statisticians compile data about the entire population (an operation called a census). This may be organized by governmental statistical institutes. Descriptive statistics can be used to summarize the population data. Numerical descriptors include mean and standard deviation for continuous data (like income), while frequency and percentage are more useful in terms of describing categorical data (like education).
When a census is not feasible, a chosen subset of the population called a sample is studied. Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. Again, descriptive statistics can be used to summarize the sample data. However, drawing the sample contains an element of randomness; hence, the numerical descriptors from the sample are also prone to uncertainty. To draw meaningful conclusions about the entire population, inferential statistics are needed. It uses patterns in the sample data to draw inferences about the population represented while accounting for randomness. These inferences may take the form of answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation), and modeling relationships within the data (for example, using regression analysis). Inference can extend to the forecasting, prediction, and estimation of unobserved values either in or associated with the population being studied. It can include extrapolation and interpolation of time series or spatial data, as well as data mining.
Mathematical statistics
[edit]Mathematical statistics is the application of mathematics to statistics. Mathematical techniques used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure-theoretic probability theory.[12][13]
History
[edit]
Formal discussions on inference date back to Arab mathematicians and cryptographers, during the Islamic Golden Age between the 8th and 13th centuries. Al-Khalil (717–786) wrote the Book of Cryptographic Messages, which contains one of the first uses of permutations and combinations, to list all possible Arabic words with and without vowels.[14] Al-Kindi's Manuscript on Deciphering Cryptographic Messages gave a detailed description of how to use frequency analysis to decipher encrypted messages, providing an early example of statistical inference for decoding. Ibn Adlan (1187–1268) later made an important contribution on the use of sample size in frequency analysis.[14]
Although the term 'statistic' was introduced by the Italian scholar Girolamo Ghilini in 1589 with reference to a collection of facts and information about a state, it was the German Gottfried Achenwall in 1749 who started using the term as a collection of quantitative information, in the modern use for this science.[15][16] The earliest writing containing statistics in Europe dates back to 1663, with the publication of Natural and Political Observations upon the Bills of Mortality by John Graunt.[17] Early applications of statistical thinking revolved around the needs of states to base policy on demographic and economic data, hence its stat- etymology. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general. Today, statistics is widely employed in government, business, and natural and social sciences.

The mathematical foundations of statistics developed from discussions concerning games of chance among mathematicians such as Gerolamo Cardano, Blaise Pascal, Pierre de Fermat, and Christiaan Huygens. Although the idea of probability was already examined in ancient and medieval law and philosophy (such as the work of Juan Caramuel), probability theory as a mathematical discipline only took shape at the very end of the 17th century, particularly in Jacob Bernoulli's posthumous work Ars Conjectandi.[18] This was the first book where the realm of games of chance and the realm of the probable (which concerned opinion, evidence, and argument) were combined and submitted to mathematical analysis.[19][20] The method of least squares was first described by Adrien-Marie Legendre in 1805, though Carl Friedrich Gauss presumably made use of it a decade earlier in 1795.[21]

The modern field of statistics emerged in the late 19th and early 20th century in three stages.[22] The first wave, at the turn of the century, was led by the work of Francis Galton and Karl Pearson, who transformed statistics into a rigorous mathematical discipline used for analysis, not just in science, but in industry and politics as well. Galton's contributions included introducing the concepts of standard deviation, correlation, regression analysis and the application of these methods to the study of the variety of human characteristics—height, weight and eyelash length among others.[23] Pearson developed the Pearson product-moment correlation coefficient, defined as a product-moment,[24] the method of moments for the fitting of distributions to samples and the Pearson distribution, among many other things.[25] Galton and Pearson founded Biometrika as the first journal of mathematical statistics and biostatistics (then called biometry), and the latter founded the world's first university statistics department at University College London.[26]
The second wave of the 1910s and 20s was initiated by William Sealy Gosset, and reached its culmination in the insights of Ronald Fisher, who wrote the textbooks that were to define the academic discipline in universities around the world. Fisher's most important publications were his 1918 seminal paper The Correlation between Relatives on the Supposition of Mendelian Inheritance (which was the first to use the statistical term, variance), his classic 1925 work Statistical Methods for Research Workers and his 1935 The Design of Experiments,[27][28][29] where he developed rigorous design of experiments models. He originated the concepts of sufficiency, ancillary statistics, Fisher's linear discriminator and Fisher information.[30] He also coined the term null hypothesis during the Lady tasting tea experiment, which "is never proved or established, but is possibly disproved, in the course of experimentation".[31][32] In his 1930 book The Genetical Theory of Natural Selection, he applied statistics to various biological concepts such as Fisher's principle[33] (which A. W. F. Edwards called "probably the most celebrated argument in evolutionary biology") and Fisherian runaway,[34][35][36][37][38][39] a concept in sexual selection about a positive feedback runaway effect found in evolution.
The final wave, which mainly saw the refinement and expansion of earlier developments, emerged from the collaborative work between Egon Pearson and Jerzy Neyman in the 1930s. They introduced the concepts of "Type II" error, power of a test and confidence intervals. Jerzy Neyman in 1934 showed that stratified random sampling was in general a better method of estimation than purposive (quota) sampling.[40]
Today, statistical methods are applied in all fields that involve decision making, for making accurate inferences from a collated body of data and for making decisions in the face of uncertainty based on statistical methodology. The use of modern computers has expedited large-scale statistical computations and has also made possible new methods that are impractical to perform manually. Statistics continues to be an area of active research, for example on the problem of how to analyze big data.[41]
Statistical data
[edit]Data collection
[edit]Sampling
[edit]When full census data cannot be collected, statisticians collect sample data by developing specific experiment designs and survey samples. Statistics itself also provides tools for prediction and forecasting through statistical models.
To use a sample as a guide to an entire population, it is important that it truly represents the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any bias within the sample and data collection procedures. There are also methods of experimental design that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population.
Sampling theory is part of the mathematical discipline of probability theory. Probability is used in mathematical statistics to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method. The difference in point of view between classic probability theory and sampling theory is, roughly, that probability theory starts from the given parameters of a total population to deduce probabilities that pertain to samples. Statistical inference, however, moves in the opposite direction—inductively inferring from samples to the parameters of a larger or total population.
Experimental and observational studies
[edit]A common goal for a statistical research project is to investigate causality, and in particular to draw a conclusion on the effect of changes in the values of predictors or independent variables on dependent variables. There are two major types of causal statistical studies: experimental studies and observational studies. In both types of studies, the effect of differences of an independent variable (or variables) on the behavior of the dependent variable are observed. The difference between the two types lies in how the study is actually conducted. Each can be very effective. An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements with different levels using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation. Instead, data are gathered and correlations between predictors and response are investigated. While the tools of data analysis work best on data from randomized studies, they are also applied to other kinds of data—like natural experiments and observational studies[42]—for which a statistician would use a modified, more structured estimation method (e.g., difference in differences estimation and instrumental variables, among many others) that produce consistent estimators.
Experiments
[edit]The basic steps of a statistical experiment are:
- Planning the research, including finding the number of replicates of the study, using the following information: preliminary estimates regarding the size of treatment effects, alternative hypotheses, and the estimated experimental variability. Consideration of the selection of experimental subjects and the ethics of research is necessary. Statisticians recommend that experiments compare (at least) one new treatment with a standard treatment or control, to allow an unbiased estimate of the difference in treatment effects.
- Design of experiments, using blocking to reduce the influence of confounding variables, and randomized assignment of treatments to subjects to allow unbiased estimates of treatment effects and experimental error. At this stage, the experimenters and statisticians write the experimental protocol that will guide the performance of the experiment and which specifies the primary analysis of the experimental data.
- Performing the experiment following the experimental protocol and analyzing the data following the experimental protocol.
- Further examining the data set in secondary analyses, to suggest new hypotheses for future study.
- Documenting and presenting the results of the study.
Experiments on human behavior have special concerns. The famous Hawthorne study examined changes to the working environment at the Hawthorne plant of the Western Electric Company. The researchers were interested in determining whether increased illumination would increase the productivity of the assembly line workers. The researchers first measured the productivity in the plant, then modified the illumination in an area of the plant and checked if the changes in illumination affected productivity. It turned out that productivity indeed improved (under the experimental conditions). However, the study is heavily criticized today for errors in experimental procedures, specifically for the lack of a control group and blindness. The Hawthorne effect refers to finding that an outcome (in this case, worker productivity) changed due to observation itself. Those in the Hawthorne study became more productive not because the lighting was changed but because they were being observed.[43]
Observational study
[edit]An example of an observational study is one that explores the association between smoking and lung cancer. This type of study typically uses a survey to collect observations about the area of interest and then performs statistical analysis. In this case, the researchers would collect observations of both smokers and non-smokers, perhaps through a cohort study, and then look for the number of cases of lung cancer in each group.[44] A case-control study is another type of observational study in which people with and without the outcome of interest (e.g. lung cancer) are invited to participate and their exposure histories are collected.
Types of data
[edit]Various attempts have been made to produce a taxonomy of levels of measurement. The psychophysicist Stanley Smith Stevens defined nominal, ordinal, interval, and ratio scales. Nominal measurements do not have meaningful rank order among values, and permit any one-to-one (injective) transformation. Ordinal measurements have imprecise differences between consecutive values, but have a meaningful order to those values, and permit any order-preserving transformation. Interval measurements have meaningful distances between measurements defined, but the zero value is arbitrary (as in the case with longitude and temperature measurements in Celsius or Fahrenheit), and permit any linear transformation. Ratio measurements have both a meaningful zero value and the distances between different measurements defined, and permit any rescaling transformation.
Because variables conforming only to nominal or ordinal measurements cannot be reasonably measured numerically, sometimes they are grouped together as categorical variables, whereas ratio and interval measurements are grouped together as quantitative variables, which can be either discrete or continuous, due to their numerical nature. Such distinctions can often be loosely correlated with data type in computer science, in that dichotomous categorical variables may be represented with the Boolean data type, polytomous categorical variables with arbitrarily assigned integers in the integral data type, and continuous variables with the real data type involving floating-point arithmetic. But the mapping of computer science data types to statistical data types depends on which categorization of the latter is being implemented.
Other categorizations have been proposed. For example, Mosteller and Tukey (1977)[45] distinguished grades, ranks, counted fractions, counts, amounts, and balances. Nelder (1990)[46] described continuous counts, continuous ratios, count ratios, and categorical modes of data. (See also: Chrisman (1998),[47] van den Berg (1991).[48])
The issue of whether or not it is appropriate to apply different kinds of statistical methods to data obtained from different kinds of measurement procedures is complicated by issues concerning the transformation of variables and the precise interpretation of research questions. "The relationship between the data and what they describe merely reflects the fact that certain kinds of statistical statements may have truth values which are not invariant under some transformations. Whether or not a transformation is sensible to contemplate depends on the question one is trying to answer."[49]: 82
Methods
[edit]Descriptive statistics
[edit]A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features of a collection of information,[50] while descriptive statistics in the mass noun sense is the process of using and analyzing those statistics. Descriptive statistics is distinguished from inferential statistics (or inductive statistics), in that descriptive statistics aims to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent.[51]
Inferential statistics
[edit]Statistical inference is the process of using data analysis to deduce properties of an underlying probability distribution.[52] Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population.[53]
Terminology and theory of inferential statistics
[edit]Statistics, estimators and pivotal quantities
[edit]Consider independent identically distributed (IID) random variables with a given probability distribution: standard statistical inference and estimation theory defines a random sample as the random vector given by the column vector of these IID variables.[54] The population being examined is described by a probability distribution that may have unknown parameters.
A statistic is a random variable that is a function of the random sample, but not a function of unknown parameters. The probability distribution of the statistic, though, may have unknown parameters. Consider now a function of the unknown parameter: an estimator is a statistic used to estimate such function. Commonly used estimators include sample mean, unbiased sample variance and sample covariance.
A random variable that is a function of the random sample and of the unknown parameter, but whose probability distribution does not depend on the unknown parameter is called a pivotal quantity or pivot. Widely used pivots include the z-score, the chi square statistic and Student's t-value.
Between two estimators of a given parameter, the one with lower mean squared error is said to be more efficient. Furthermore, an estimator is said to be unbiased if its expected value is equal to the true value of the unknown parameter being estimated, and asymptotically unbiased if its expected value converges at the limit to the true value of such parameter.
Other desirable properties for estimators include: UMVUE estimators that have the lowest variance for all possible values of the parameter to be estimated (this is usually an easier property to verify than efficiency) and consistent estimators which converges in probability to the true value of such parameter.
This still leaves the question of how to obtain estimators in a given situation and carry the computation, several methods have been proposed: the method of moments, the maximum likelihood method, the least squares method and the more recent method of estimating equations.
Null hypothesis and alternative hypothesis
[edit]Interpretation of statistical information can often involve the development of a null hypothesis which is usually (but not necessarily) that no relationship exists among variables or that no change occurred over time.[55][56]
The best illustration for a novice is the predicament encountered by a criminal trial. The null hypothesis, H0, asserts that the defendant is innocent, whereas the alternative hypothesis, H1, asserts that the defendant is guilty. The indictment comes because of suspicion of the guilt. The H0 (status quo) stands in opposition to H1 and is maintained unless H1 is supported by evidence "beyond a reasonable doubt". However, "failure to reject H0" in this case does not imply innocence, but merely that the evidence was insufficient to convict. So the jury does not necessarily accept H0 but fails to reject H0. While one can not "prove" a null hypothesis, one can test how close it is to being true with a power test, which tests for type II errors.
What statisticians call an alternative hypothesis is simply a hypothesis that contradicts the null hypothesis.
Error
[edit]Working from a null hypothesis, two broad categories of error are recognized:
- Type I errors where the null hypothesis is falsely rejected, giving a "false positive".
- Type II errors where the null hypothesis fails to be rejected and an actual difference between populations is missed, giving a "false negative".
Standard deviation refers to the extent to which individual observations in a sample differ from a central value, such as the sample or population mean, while Standard error refers to an estimate of difference between sample mean and population mean.
A statistical error is the amount by which an observation differs from its expected value. A residual is the amount an observation differs from the value the estimator of the expected value assumes on a given sample (also called prediction).
Mean squared error is used for obtaining efficient estimators, a widely used class of estimators. Root mean square error is simply the square root of mean squared error.
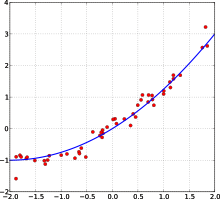
Many statistical methods seek to minimize the residual sum of squares, and these are called "methods of least squares" in contrast to Least absolute deviations. The latter gives equal weight to small and big errors, while the former gives more weight to large errors. Residual sum of squares is also differentiable, which provides a handy property for doing regression. Least squares applied to linear regression is called ordinary least squares method and least squares applied to nonlinear regression is called non-linear least squares. Also in a linear regression model the non deterministic part of the model is called error term, disturbance or more simply noise. Both linear regression and non-linear regression are addressed in polynomial least squares, which also describes the variance in a prediction of the dependent variable (y axis) as a function of the independent variable (x axis) and the deviations (errors, noise, disturbances) from the estimated (fitted) curve.
Measurement processes that generate statistical data are also subject to error. Many of these errors are classified as random (noise) or systematic (bias), but other types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also be important. The presence of missing data or censoring may result in biased estimates and specific techniques have been developed to address these problems.[57]
Interval estimation
[edit]
Most studies only sample part of a population, so results do not fully represent the whole population. Any estimates obtained from the sample only approximate the population value. Confidence intervals allow statisticians to express how closely the sample estimate matches the true value in the whole population. Often they are expressed as 95% confidence intervals. Formally, a 95% confidence interval for a value is a range where, if the sampling and analysis were repeated under the same conditions (yielding a different dataset), the interval would include the true (population) value in 95% of all possible cases. This does not imply that the probability that the true value is in the confidence interval is 95%. From the frequentist perspective, such a claim does not even make sense, as the true value is not a random variable. Either the true value is or is not within the given interval. However, it is true that, before any data are sampled and given a plan for how to construct the confidence interval, the probability is 95% that the yet-to-be-calculated interval will cover the true value: at this point, the limits of the interval are yet-to-be-observed random variables. One approach that does yield an interval that can be interpreted as having a given probability of containing the true value is to use a credible interval from Bayesian statistics: this approach depends on a different way of interpreting what is meant by "probability", that is as a Bayesian probability.
In principle confidence intervals can be symmetrical or asymmetrical. An interval can be asymmetrical because it works as lower or upper bound for a parameter (left-sided interval or right sided interval), but it can also be asymmetrical because the two sided interval is built violating symmetry around the estimate. Sometimes the bounds for a confidence interval are reached asymptotically and these are used to approximate the true bounds.
Significance
[edit]Statistics rarely give a simple Yes/No type answer to the question under analysis. Interpretation often comes down to the level of statistical significance applied to the numbers and often refers to the probability of a value accurately rejecting the null hypothesis (sometimes referred to as the p-value).
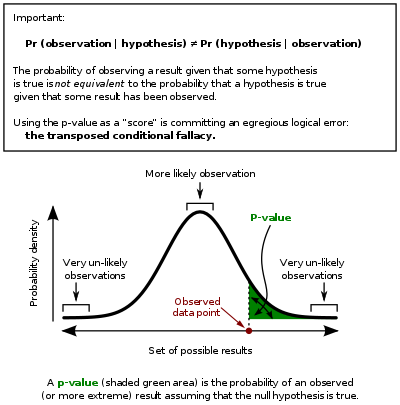
The standard approach[54] is to test a null hypothesis against an alternative hypothesis. A critical region is the set of values of the estimator that leads to refuting the null hypothesis. The probability of type I error is therefore the probability that the estimator belongs to the critical region given that null hypothesis is true (statistical significance) and the probability of type II error is the probability that the estimator does not belong to the critical region given that the alternative hypothesis is true. The statistical power of a test is the probability that it correctly rejects the null hypothesis when the null hypothesis is false.
Referring to statistical significance does not necessarily mean that the overall result is significant in real world terms. For example, in a large study of a drug it may be shown that the drug has a statistically significant but very small beneficial effect, such that the drug is unlikely to help the patient noticeably.
Although in principle the acceptable level of statistical significance may be subject to debate, the significance level is the largest p-value that allows the test to reject the null hypothesis. This test is logically equivalent to saying that the p-value is the probability, assuming the null hypothesis is true, of observing a result at least as extreme as the test statistic. Therefore, the smaller the significance level, the lower the probability of committing type I error.
Some problems are usually associated with this framework (See criticism of hypothesis testing):
- A difference that is highly statistically significant can still be of no practical significance, but it is possible to properly formulate tests to account for this. One response involves going beyond reporting only the significance level to include the p-value when reporting whether a hypothesis is rejected or accepted. The p-value, however, does not indicate the size or importance of the observed effect and can also seem to exaggerate the importance of minor differences in large studies. A better and increasingly common approach is to report confidence intervals. Although these are produced from the same calculations as those of hypothesis tests or p-values, they describe both the size of the effect and the uncertainty surrounding it.
- Fallacy of the transposed conditional, aka prosecutor's fallacy: criticisms arise because the hypothesis testing approach forces one hypothesis (the null hypothesis) to be favored, since what is being evaluated is the probability of the observed result given the null hypothesis and not probability of the null hypothesis given the observed result. An alternative to this approach is offered by Bayesian inference, although it requires establishing a prior probability.[58]
- Rejecting the null hypothesis does not automatically prove the alternative hypothesis.
- As everything in inferential statistics it relies on sample size, and therefore under fat tails p-values may be seriously mis-computed.[clarification needed]
Examples
[edit]Some well-known statistical tests and procedures are:
Exploratory data analysis
[edit]Exploratory data analysis (EDA) is an approach to analyzing data sets to summarize their main characteristics, often with visual methods. A statistical model can be used or not, but primarily EDA is for seeing what the data can tell us beyond the formal modeling or hypothesis testing task.
Misuse
[edit]Misuse of statistics can produce subtle but serious errors in description and interpretation—subtle in the sense that even experienced professionals make such errors, and serious in the sense that they can lead to devastating decision errors. For instance, social policy, medical practice, and the reliability of structures like bridges all rely on the proper use of statistics.
Even when statistical techniques are correctly applied, the results can be difficult to interpret for those lacking expertise. The statistical significance of a trend in the data—which measures the extent to which a trend could be caused by random variation in the sample—may or may not agree with an intuitive sense of its significance. The set of basic statistical skills (and skepticism) that people need to deal with information in their everyday lives properly is referred to as statistical literacy.
There is a general perception that statistical knowledge is all-too-frequently intentionally misused by finding ways to interpret only the data that are favorable to the presenter.[59] A mistrust and misunderstanding of statistics is associated with the quotation, "There are three kinds of lies: lies, damned lies, and statistics". Misuse of statistics can be both inadvertent and intentional, and the book How to Lie with Statistics,[59] by Darrell Huff, outlines a range of considerations. In an attempt to shed light on the use and misuse of statistics, reviews of statistical techniques used in particular fields are conducted (e.g. Warne, Lazo, Ramos, and Ritter (2012)).[60]
Ways to avoid misuse of statistics include using proper diagrams and avoiding bias.[61] Misuse can occur when conclusions are overgeneralized and claimed to be representative of more than they really are, often by either deliberately or unconsciously overlooking sampling bias.[62] Bar graphs are arguably the easiest diagrams to use and understand, and they can be made either by hand or with simple computer programs.[61] Most people do not look for bias or errors, so they are not noticed. Thus, people may often believe that something is true even if it is not well represented.[62] To make data gathered from statistics believable and accurate, the sample taken must be representative of the whole.[63] According to Huff, "The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism."[64]
To assist in the understanding of statistics Huff proposed a series of questions to be asked in each case:[59]
- Who says so? (Does he/she have an axe to grind?)
- How does he/she know? (Does he/she have the resources to know the facts?)
- What's missing? (Does he/she give us a complete picture?)
- Did someone change the subject? (Does he/she offer us the right answer to the wrong problem?)
- Does it make sense? (Is his/her conclusion logical and consistent with what we already know?)
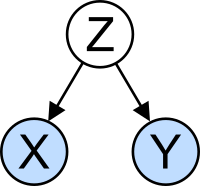
Misinterpretation: correlation
[edit]The concept of correlation is particularly noteworthy for the potential confusion it can cause. Statistical analysis of a data set often reveals that two variables (properties) of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death, might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation phenomena could be caused by a third, previously unconsidered phenomenon, called a lurking variable or confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables.
Applications
[edit]Applied statistics, theoretical statistics and mathematical statistics
[edit]Applied statistics, sometimes referred to as Statistical science,[65] comprises descriptive statistics and the application of inferential statistics.[66][67] Theoretical statistics concerns the logical arguments underlying justification of approaches to statistical inference, as well as encompassing mathematical statistics. Mathematical statistics includes not only the manipulation of probability distributions necessary for deriving results related to methods of estimation and inference, but also various aspects of computational statistics and the design of experiments.
Statistical consultants can help organizations and companies that do not have in-house expertise relevant to their particular questions.
Machine learning and data mining
[edit]Machine learning models are statistical and probabilistic models that capture patterns in the data through use of computational algorithms.
Statistics in academia
[edit]Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences, government, and business. Business statistics applies statistical methods in econometrics, auditing and production and operations, including services improvement and marketing research.[68] A study of two journals in tropical biology found that the 12 most frequent statistical tests are: analysis of variance (ANOVA), chi-squared test, Student's t-test, linear regression, Pearson's correlation coefficient, Mann-Whitney U test, Kruskal-Wallis test, Shannon's diversity index, Tukey's range test, cluster analysis, Spearman's rank correlation coefficient and principal component analysis.[69]
A typical statistics course covers descriptive statistics, probability, binomial and normal distributions, test of hypotheses and confidence intervals, linear regression, and correlation.[70] Modern fundamental statistical courses for undergraduate students focus on correct test selection, results interpretation, and use of free statistics software.[69]
Statistical computing
[edit]
The rapid and sustained increases in computing power starting from the second half of the 20th century have had a substantial impact on the practice of statistical science. Early statistical models were almost always from the class of linear models, but powerful computers, coupled with suitable numerical algorithms, caused an increased interest in nonlinear models (such as neural networks) as well as the creation of new types, such as generalized linear models and multilevel models.
Increased computing power has also led to the growing popularity of computationally intensive methods based on resampling, such as permutation tests and the bootstrap, while techniques such as Gibbs sampling have made use of Bayesian models more feasible. The computer revolution has implications for the future of statistics with a new emphasis on "experimental" and "empirical" statistics. A large number of both general and special purpose statistical software are now available. Examples of available software capable of complex statistical computation include programs such as Mathematica, SAS, SPSS, and R.
Business statistics
[edit]In business, "statistics" is a widely used management- and decision support tool. It is particularly applied in financial management, marketing management, and production, services and operations management .[71][72] Statistics is also heavily used in management accounting and auditing. The discipline of Management Science formalizes the use of statistics, and other mathematics, in business. (Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships.)
A typical "Business Statistics" course is intended for business majors, and covers [73] descriptive statistics (collection, description, analysis, and summary of data), probability (typically the binomial and normal distributions), test of hypotheses and confidence intervals, linear regression, and correlation; (follow-on) courses may include forecasting, time series, decision trees, multiple linear regression, and other topics from business analytics more generally. See also Business mathematics § University level. Professional certification programs, such as the CFA, often include topics in statistics.
Statistics applied to mathematics or the arts
[edit]Traditionally, statistics was concerned with drawing inferences using a semi-standardized methodology that was "required learning" in most sciences. This tradition has changed with the use of statistics in non-inferential contexts. What was once considered a dry subject, taken in many fields as a degree-requirement, is now viewed enthusiastically.[according to whom?] Initially derided by some mathematical purists, it is now considered essential methodology in certain areas.
- In number theory, scatter plots of data generated by a distribution function may be transformed with familiar tools used in statistics to reveal underlying patterns, which may then lead to hypotheses.
- Predictive methods of statistics in forecasting combining chaos theory and fractal geometry can be used to create video works.[74]
- The process art of Jackson Pollock relied on artistic experiments whereby underlying distributions in nature were artistically revealed.[75] With the advent of computers, statistical methods were applied to formalize such distribution-driven natural processes to make and analyze moving video art.[citation needed]
- Methods of statistics may be used predicatively in performance art, as in a card trick based on a Markov process that only works some of the time, the occasion of which can be predicted using statistical methodology.
- Statistics can be used to predicatively create art, as in the statistical or stochastic music invented by Iannis Xenakis, where the music is performance-specific. Though this type of artistry does not always come out as expected, it does behave in ways that are predictable and tunable using statistics.
Specialized disciplines
[edit]Statistical techniques are used in a wide range of types of scientific and social research, including: biostatistics, computational biology, computational sociology, network biology, social science, sociology and social research. Some fields of inquiry use applied statistics so extensively that they have specialized terminology. These disciplines include:
- Actuarial science (assesses risk in the insurance and finance industries)
- Applied information economics
- Astrostatistics (statistical evaluation of astronomical data)
- Biostatistics
- Chemometrics (for analysis of data from chemistry)
- Data mining (applying statistics and pattern recognition to discover knowledge from data)
- Data science ()
- Demography (statistical study of populations)
- Econometrics (statistical analysis of economic data)
- Energy statistics
- Engineering statistics
- Epidemiology (statistical analysis of disease)
- Geography and geographic information systems, specifically in spatial analysis
- Image processing
- Jurimetrics (law)
- Medical statistics
- Political science
- Psychological statistics
- Reliability engineering
- Social statistics
- Statistical mechanics
In addition, there are particular types of statistical analysis that have also developed their own specialised terminology and methodology:
- Bootstrap / jackknife resampling
- Multivariate statistics
- Statistical classification
- Structured data analysis
- Structural equation modelling
- Survey methodology
- Survival analysis
- Statistics in various sports, particularly baseball – known as sabermetrics – and cricket
Statistics form a key basis tool in business and manufacturing as well. It is used to understand measurement systems variability, control processes (as in statistical process control or SPC), for summarizing data, and to make data-driven decisions.
See also
[edit]- Abundance estimation
- Glossary of probability and statistics
- List of academic statistical associations
- List of important publications in statistics
- List of national and international statistical services
- List of statistical packages (software)
- List of statistics articles
- List of university statistical consulting centers
- Notation in probability and statistics
- Statistics education
- World Statistics Day
- Robust statistics
- Foundations and major areas of statistics
- Philosophy of statistics
- Probability interpretations
- Foundations of statistics
- List of statisticians
- Official statistics
- Multivariate analysis of variance
References
[edit]- ^ "statistics". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ "Statistik" in Digitales Wörterbuch der deutschen Sprache
- ^ "Statistics". Oxford Reference. Oxford University Press. January 2008. ISBN 978-0-19-954145-4. Archived from the original on 2020-09-03. Retrieved 2019-08-14.
- ^ Romijn, Jan-Willem (2014). "Philosophy of statistics". Stanford Encyclopedia of Philosophy. Archived from the original on 2021-10-19. Retrieved 2016-11-03.
- ^ "Cambridge Dictionary". Archived from the original on 2020-11-22. Retrieved 2019-08-14.
- ^ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, Oxford University Press. ISBN 0-19-920613-9
- ^ a b Lund Research Ltd. "Descriptive and Inferential Statistics". statistics.laerd.com. Archived from the original on 2020-10-26. Retrieved 2014-03-23.
- ^ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5. pp. 1–3
- ^ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p. xii, ISBN 978-0-03-077945-9
- ^ Moore, David (1992). "Teaching Statistics as a Respectable Subject". In F. Gordon; S. Gordon (eds.). Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14–25. ISBN 978-0-88385-078-7.
- ^ Chance, Beth L.; Rossman, Allan J. (2005). "Preface" (PDF). Investigating Statistical Concepts, Applications, and Methods. Duxbury Press. ISBN 978-0-495-05064-3. Archived (PDF) from the original on 2020-11-22. Retrieved 2009-12-06.
- ^ Lakshmikantham, D.; Kannan, V. (2002). Handbook of stochastic analysis and applications. New York: M. Dekker. ISBN 0824706609.
- ^ Schervish, Mark J. (1995). Theory of statistics (Corr. 2nd print. ed.). New York: Springer. ISBN 0387945466.
- ^ a b Broemeling, Lyle D. (1 November 2011). "An Account of Early Statistical Inference in Arab Cryptology". The American Statistician. 65 (4): 255–257. doi:10.1198/tas.2011.10191. S2CID 123537702.
- ^ Ostasiewicz, Walenty (2014). "The emergence of statistical science". Śląski Przegląd Statystyczny. 12 (18): 76–77. doi:10.15611/sps.2014.12.04.
- ^ Bruneau, Quentin (2022). States and the Masters of Capital: Sovereign Lending, Old and New. Columbia University Press. ISBN 978-0231555647.
- ^ Willcox, Walter (1938) "The Founder of Statistics". Review of the International Statistical Institute 5(4): 321–328. JSTOR 1400906
- ^ J. Franklin, The Science of Conjecture: Evidence and Probability before Pascal, Johns Hopkins Univ Pr 2002
- ^ Schneider, I. (2005). Jakob Bernoulli, Ars Conjectandi (1713). In I. Grattan-Guinness (Ed.), Landmark writings in Western Mathematics, 1640-1940 (pp. 88-103).
- ^ Sylla, E. D.; Bernoulli, Jacob (2006). The Art of Conjecturing, Together with Letter to a Friend on Sets in Court Tennis (trans.). JHU Press. ISBN 978-0-8018-8235-7.
- ^ Lim, M. (2021). "Gauss, Least Squares, and the Missing Planet". Actuaries Digital. Retrieved 2022-11-01.
- ^ Helen Mary Walker (1975). Studies in the history of statistical method. Arno Press. ISBN 978-0405066283. Archived from the original on 2020-07-27. Retrieved 2015-06-27.
- ^ Galton, F (1877). "Typical laws of heredity". Nature. 15 (388): 492–553. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0.
- ^ Stigler, S.M. (1989). "Francis Galton's Account of the Invention of Correlation". Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580.
- ^ Pearson, K. (1900). "On the Criterion that a given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be reasonably supposed to have arisen from Random Sampling". Philosophical Magazine. Series 5. 50 (302): 157–175. doi:10.1080/14786440009463897. Archived from the original on 2020-08-18. Retrieved 2019-06-27.
- ^ "Karl Pearson (1857–1936)". Department of Statistical Science – University College London. Archived from the original on 2008-09-25.
- ^ Box, JF (February 1980). "R.A. Fisher and the Design of Experiments, 1922–1926". The American Statistician. 34 (1): 1–7. doi:10.2307/2682986. JSTOR 2682986.
- ^ Yates, F (June 1964). "Sir Ronald Fisher and the Design of Experiments". Biometrics. 20 (2): 307–321. doi:10.2307/2528399. JSTOR 2528399.
- ^ Stanley, Julian C. (1966). "The Influence of Fisher's "The Design of Experiments" on Educational Research Thirty Years Later". American Educational Research Journal. 3 (3): 223–229. doi:10.3102/00028312003003223. JSTOR 1161806. S2CID 145725524.
- ^ Agresti, Alan; David B. Hichcock (2005). "Bayesian Inference for Categorical Data Analysis" (PDF). Statistical Methods & Applications. 14 (3): 298. doi:10.1007/s10260-005-0121-y. S2CID 18896230. Archived (PDF) from the original on 2013-12-19. Retrieved 2013-12-19.
- ^ OED quote: 1935 R.A. Fisher, The Design of Experiments ii. 19, "We may speak of this hypothesis as the 'null hypothesis', and the null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation."
- ^ Fisher|1971|loc=Chapter II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment, Section 8. The Null Hypothesis
- ^ Edwards, A.W.F. (1998). "Natural Selection and the Sex Ratio: Fisher's Sources". American Naturalist. 151 (6): 564–569. doi:10.1086/286141. PMID 18811377. S2CID 40540426.
- ^ Fisher, R.A. (1915) The evolution of sexual preference. Eugenics Review (7) 184:192
- ^ Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3
- ^ Edwards, A.W.F. (2000) Perspectives: Anecdotal, Historical and Critical Commentaries on Genetics. The Genetics Society of America (154) 1419:1426
- ^ Andersson, Malte (1994). Sexual Selection. Princeton University Press. ISBN 0-691-00057-3. Archived from the original on 2019-12-25. Retrieved 2019-09-19.
- ^ Andersson, M. and Simmons, L.W. (2006) Sexual selection and mate choice. Trends, Ecology and Evolution (21) 296:302
- ^ Gayon, J. (2010) Sexual selection: Another Darwinian process. Comptes Rendus Biologies (333) 134:144
- ^ Neyman, J (1934). "On the two different aspects of the representative method: The method of stratified sampling and the method of purposive selection". Journal of the Royal Statistical Society. 97 (4): 557–625. doi:10.2307/2342192. JSTOR 2342192.
- ^ "Science in a Complex World – Big Data: Opportunity or Threat?". Santa Fe Institute. 2 December 2013. Archived from the original on 2016-05-30. Retrieved 2014-10-13.
- ^ Freedman, D.A. (2005) Statistical Models: Theory and Practice, Cambridge University Press. ISBN 978-0-521-67105-7
- ^ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P (2007). "The Hawthorne Effect: a randomised, controlled trial". BMC Med Res Methodol. 7 (1): 30. doi:10.1186/1471-2288-7-30. PMC 1936999. PMID 17608932.
- ^ Rothman, Kenneth J; Greenland, Sander; Lash, Timothy, eds. (2008). "7". Modern Epidemiology (3rd ed.). Lippincott Williams & Wilkins. p. 100. ISBN 978-0781755641.
- ^ Mosteller, F.; Tukey, J.W (1977). Data analysis and regression. Boston: Addison-Wesley.
- ^ Nelder, J.A. (1990). The knowledge needed to computerise the analysis and interpretation of statistical information. In Expert systems and artificial intelligence: the need for information about data. Library Association Report, London, March, 23–27.
- ^ Chrisman, Nicholas R (1998). "Rethinking Levels of Measurement for Cartography". Cartography and Geographic Information Science. 25 (4): 231–242. Bibcode:1998CGISy..25..231C. doi:10.1559/152304098782383043.
- ^ van den Berg, G. (1991). Choosing an analysis method. Leiden: DSWO Press
- ^ Hand, D.J. (2004). Measurement theory and practice: The world through quantification. London: Arnold.
- ^ Mann, Prem S. (1995). Introductory Statistics (2nd ed.). Wiley. ISBN 0-471-31009-3.
- ^ "Descriptive Statistics | Research Connections". www.researchconnections.org. Retrieved 2023-01-10.
- ^ Upton, G., Cook, I. (2008) Oxford Dictionary of Statistics, OUP. ISBN 978-0-19-954145-4.
- ^ "Basic Inferential Statistics - Purdue OWL® - Purdue University". owl.purdue.edu. Retrieved 2023-01-10.
- ^ a b Piazza Elio, Probabilità e Statistica, Esculapio 2007
- ^ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 0521593468.
- ^ "Cohen (1994) The Earth Is Round (p < .05)". YourStatsGuru.com. Archived from the original on 2015-09-05. Retrieved 2015-07-20.
- ^ Rubin, Donald B.; Little, Roderick J.A., Statistical analysis with missing data, New York: Wiley 2002
- ^ Ioannidis, J.P.A. (2005). "Why Most Published Research Findings Are False". PLOS Medicine. 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMC 1182327. PMID 16060722.
- ^ a b c Huff, Darrell (1954) How to Lie with Statistics, WW Norton & Company, Inc. New York. ISBN 0-393-31072-8
- ^ Warne, R. Lazo; Ramos, T.; Ritter, N. (2012). "Statistical Methods Used in Gifted Education Journals, 2006–2010". Gifted Child Quarterly. 56 (3): 134–149. doi:10.1177/0016986212444122. S2CID 144168910.
- ^ a b Drennan, Robert D. (2008). "Statistics in archaeology". In Pearsall, Deborah M. (ed.). Encyclopedia of Archaeology. Elsevier Inc. pp. 2093–2100. ISBN 978-0-12-373962-9.
- ^ a b Cohen, Jerome B. (December 1938). "Misuse of Statistics". Journal of the American Statistical Association. 33 (204). JSTOR: 657–674. doi:10.1080/01621459.1938.10502344.
- ^ Freund, J.E. (1988). "Modern Elementary Statistics". Credo Reference.
- ^ Huff, Darrell; Irving Geis (1954). How to Lie with Statistics. New York: Norton.
The dependability of a sample can be destroyed by [bias]... allow yourself some degree of skepticism.
- ^ Nelder, John A. (1999). "From Statistics to Statistical Science". Journal of the Royal Statistical Society. Series D (The Statistician). 48 (2): 257–269. doi:10.1111/1467-9884.00187. ISSN 0039-0526. JSTOR 2681191. Archived from the original on 2022-01-15. Retrieved 2022-01-15.
- ^ Nikoletseas, M.M. (2014) "Statistics: Concepts and Examples." ISBN 978-1500815684
- ^ Anderson, D.R.; Sweeney, D.J.; Williams, T.A. (1994) Introduction to Statistics: Concepts and Applications, pp. 5–9. West Group. ISBN 978-0-314-03309-3
- ^ "Journal of Business & Economic Statistics". Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 27 July 2020. Retrieved 16 March 2020.
- ^ a b Natalia Loaiza Velásquez, María Isabel González Lutz & Julián Monge-Nájera (2011). "Which statistics should tropical biologists learn?" (PDF). Revista de Biología Tropical. 59: 983–992. Archived (PDF) from the original on 2020-10-19. Retrieved 2020-04-26.
- ^ Pekoz, Erol (2009). The Manager's Guide to Statistics. Erol Pekoz. ISBN 978-0979570438.
- ^ "Aims and scope". Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 23 June 2021. Retrieved 16 March 2020.
- ^ "Journal of Business & Economic Statistics". Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 27 July 2020. Retrieved 16 March 2020.
- ^ Numerous texts are available, reflecting the scope and reach of the discipline in the business world:
- Sharpe, N. (2014). Business Statistics, Pearson. ISBN 978-0134705217
- Wegner, T. (2010). Applied Business Statistics: Methods and Excel-Based Applications, Juta Academic. ISBN 0702172863
- Holmes, L., Illowsky, B., Dean, S. (2017). Introductory Business Statistics Archived 2021-06-16 at the Wayback Machine
- Nica, M. (2013). Principles of Business Statistics Archived 2021-05-18 at the Wayback Machine
- ^ Cline, Graysen (2019). Nonparametric Statistical Methods Using R. EDTECH. ISBN 978-1-83947-325-8. OCLC 1132348139. Archived from the original on 2022-05-15. Retrieved 2021-09-16.
- ^ Palacios, Bernardo; Rosario, Alfonso; Wilhelmus, Monica M.; Zetina, Sandra; Zenit, Roberto (2019-10-30). "Pollock avoided hydrodynamic instabilities to paint with his dripping technique". PLOS ONE. 14 (10): e0223706. Bibcode:2019PLoSO..1423706P. doi:10.1371/journal.pone.0223706. ISSN 1932-6203. PMC 6821064. PMID 31665191.
Further reading
[edit]- Lydia Denworth, "A Significant Problem: Standard scientific methods are under fire. Will anything change?", Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. "The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields. There is growing determination to reform statistical analysis... Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining "significant" results." (p. 63.)
- Barbara Illowsky; Susan Dean (2014). Introductory Statistics. OpenStax CNX. ISBN 978-1938168208.
- Stockburger, David W. "Introductory Statistics: Concepts, Models, and Applications". Missouri State University (3rd Web ed.). Archived from the original on 28 May 2020.
- OpenIntro Statistics Archived 2019-06-16 at the Wayback Machine, 3rd edition by Diez, Barr, and Cetinkaya-Rundel
- Stephen Jones, 2010. Statistics in Psychology: Explanations without Equations. Palgrave Macmillan. ISBN 978-1137282392.
- Cohen, J (1990). "Things I have learned (so far)" (PDF). American Psychologist. 45 (12): 1304–1312. doi:10.1037/0003-066x.45.12.1304. S2CID 7180431. Archived from the original (PDF) on 2017-10-18.
- Gigerenzer, G (2004). "Mindless statistics". Journal of Socio-Economics. 33 (5): 587–606. doi:10.1016/j.socec.2004.09.033.
- Ioannidis, J.P.A. (2005). "Why most published research findings are false". PLOS Medicine. 2 (4): 696–701. doi:10.1371/journal.pmed.0040168. PMC 1855693. PMID 17456002.
External links
[edit]- (Electronic Version): TIBCO Software Inc. (2020). Data Science Textbook.
- Online Statistics Education: An Interactive Multimedia Course of Study. Developed by Rice University (Lead Developer), University of Houston Clear Lake, Tufts University, and National Science Foundation.
- UCLA Statistical Computing Resources (archived 17 July 2006)
- Philosophy of Statistics from the Stanford Encyclopedia of Philosophy
Major mathematics areas | |
|---|---|
| Foundations | |
| Algebra | |
| Analysis | |
| Discrete | |
| Geometry | |
| Number theory | |
| Topology | |
| Applied | |
| Computational | |
| Related topics | |