In mathematics, the Heronian mean H of two non-negative real numbers A and B is given by the formula
It is named after Hero of Alexandria.[1]
In mathematics, the Heronian mean H of two non-negative real numbers A and B is given by the formula
It is named after Hero of Alexandria.[1]
Just like all means, the Heronian mean is symmetric (it does not depend on the order in which its two arguments are given) and idempotent (the mean of any number with itself is the same number).
The Heronian mean of the numbers A and B is a weighted mean of their arithmetic and geometric means:[1]
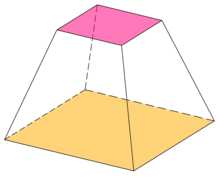
The Heronian mean may be used in finding the volume of a frustum of a pyramid or cone. The volume is equal to the product of the height of the frustum and the Heronian mean of the areas of the opposing parallel faces.[2]
A version of this formula, for square frusta, appears in the Moscow Mathematical Papyrus from Ancient Egyptian mathematics, whose content dates to roughly 1850 BC.[1][3]