Logical fallacy
The fallacy of the undistributed middle (Latin: non distributio medii) is a formal fallacy that is committed when the middle term in a categorical syllogism is not distributed in either the minor premise or the major premise. It is thus a syllogistic fallacy.
Classical formulation
In classical syllogisms, all statements consist of two terms and are in the form of "A" (all), "E" (none), "I" (some), or "O" (some not). The first term is distributed in A statements; the second is distributed in O statements; both are distributed in "E" statements, and none are distributed in I statements.
The fallacy of the undistributed middle occurs when the term that links the two premises is never distributed.
In this example, distribution is marked in boldface:
- All Z is B
- All Y is B
- Therefore, all Y is Z
B is the common term between the two premises (the middle term) but is never distributed, so this syllogism is invalid. B would be distributed by introducing a premise which states either All B is Z, or No B is Z.
Also, a related rule of logic is that anything distributed in the conclusion must be distributed in at least one premise.
- All Z is B
- Some Y is Z
- Therefore, all Y is B
The middle term—Z—is distributed, but Y is distributed in the conclusion and not in any premise, so this syllogism is invalid.
Pattern
The fallacy of the undistributed middle takes the following form:
- All Z is B
- Y is B
- Therefore, Y is Z
This may be graphically represented as follows:
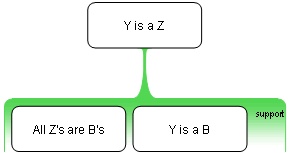
where the premises are in the green box and the conclusion is indicated above them.
B is the middle term (because it appears in both premises), and it is not distributed in the major premise, "all Z is B".
It may or may not be the case that "all Z is B," but this is irrelevant to the conclusion. What is relevant to the conclusion is whether it is true that "all B is Z," which is ignored in the argument. The fallacy is similar to affirming the consequent and denying the antecedent. However, the fallacy may be resolved if the terms are exchanged in either the conclusion or in the first co-premise. Indeed, from the perspective of first-order logic, all cases of the fallacy of the undistributed middle are, in fact, examples of affirming the consequent or denying the antecedent, depending on the structure of the fallacious argument.
Examples
For example:
- All students carry backpacks.
- My grandfather carries a backpack.
- Therefore, my grandfather is a student.
|
- All students carry backpacks.
- My grandfather carries a backpack.
- Everyone who carries a backpack is a student.
- Therefore, my grandfather is a student.
|

The middle term is the one that appears in both premises—in this case, it is the class of backpack carriers. It is undistributed because neither of its uses applies to all backpack carriers. Therefore, it cannot be used to connect students and my grandfather—both of them could be separate and unconnected divisions of the class of backpack carriers. Note below how "carries a backpack" is truly undistributed:
- grandfather is someone who carries a backpack; student is someone who carries a backpack
Specifically, the structure of this example results in affirming the consequent.
However, if the latter two statements were switched, the syllogism would be valid:
- All students carry backpacks.
- My grandfather is a student.
- Therefore, my grandfather carries a backpack.
In this case, the middle term is the class of students, and the first use clearly refers to 'all students'. It is therefore distributed across the whole of its class, and so can be used to connect the other two terms (backpack carriers, and my grandfather). Again, note below that "student" is distributed:
- grandfather is a student and thus carries a backpack
In popular culture
The fallacy of the undistributed middle is referenced in Edgar Allan Poe's detective story The Purloined Letter:
This functionary, however, has been thoroughly mystified; and the remote source of his defeat lies in the supposition that the Minister is a fool because he has acquired renown as a poet. All fools are poets; this the Prefect feels, and he is merely guilty of a non distributio medii in thence inferring that all poets are fools.
The fallacy is also referenced by Christopher Hitchens and William F. Buckley Jr. on Episode S0629 of Firing Line (TV program) recorded on December 11, 1984, at the 34 minute and 26 second (34:26) mark.[1]

