Noob Links for myself
Help pages
|
|---|
Changes[edit]
Thank you, Rschwieb, you've done a great job. You've been very kind. Serialsam (talk) 12:39, 28 April 2011 (UTC)
Proposal to merge removed. Comment added at https://en.wikipedia.org/wiki/Talk:Outline_of_algebraic_structures#Merge_proposal Yangjerng (talk) 14:03, 13 April 2012 (UTC)
Flat space gravity[edit]
Archive
|
|---|
|
I've not been working on the geometric algebra article for the time being. That does not mean I think it is in good shape; I think it still needs lots of work. I'll probably look at it again in time. I'm guessing that you may have some interest in learning about GR. If you want to exercise your (newly acquired?) geometric algebra skills, there might be something to interest you: a development of the math of relativistic gravitation in a Minkowski space background. Variations on this theme have been tried before, with some success. There are related articles around (Linearized gravity, Gravitoelectromagnetism). It might be fun to get an accurate feel of the maths behind gravity. Aside from a few presumptious leaps, the maths shows initial promise of being simple. Interested? Quondumtalkcontr 17:47, 8 December 2011 (UTC)
OK. This again reminds me that I don't know where to begin :) I guess any start is good. I'd like to understand whatever important models of electromagnetism and gravitation that exist. Rschwieb (talk) 17:15, 9 December 2011 (UTC)
|
Found a new article talking extensively about the 3-1 and 1-3 difference[3]. It'll be a while before I can look at it. Rschwieb (talk) 14:58, 16 December 2011 (UTC)
- This paper glosses over is the lack of manifest basis independence in some of the formulations. If something like the Dirac equation cannot be formulated in a manifestly basis-independent fashion, it bothers me. The (3,1) and (1,3) difference is significant in this context. I think that to explore this question by reading papers like this one in depth will diffuse your energy with little result; my inclination is to rather explore it from the persective of mathematical principles, e.g.: Can the Dirac equation be written in a manifestly basis-independent form? I suspect that as it stands it can be in the (3,1) algebra but not in (1,3); this approach should be very easy (I have in the past tackled it, and would be interested in following this route again). I also have an intriguing idea for restating the Dirac equation so that it combines all the families (electron, muon, tauon) into one equation, which if successful may give a different "preferred quadratic form" and a almost certainly a very interesting mathematical result. In any event, be aware that the question of the signature is a seriously non-trivial one; do not expect to be able to answer it. Would you like me to map a line of investigation? — Quondumtc 07:15, 17 December 2011 (UTC)
- Honestly I think even that task sounds beyond me right now :) What I really need is a review of all fundamental operations in linear algebra, in "traditional" fashion side by side with "GA fashion". Then I would need to do the same thing for vector calculus. Maybe at /Basic GA? Ideally I would do some homework problems of this sort, to refamiliarize myself with how all this works. I can't imagine tackling something like Dirac's equation when I don't even fully grasp the form or meaning of Maxwell's equations and Einstein's equations. Rschwieb (talk) 14:05, 17 December 2011 (UTC)
- I've put together my attempt at a rigorous if simplistic start at /Basic GA to make sure we have the basics sutiably defined. Now perhaps we can work out what it is you want to review – point me in a direction and I'll see whether I can be useful. I'm not too sure how linear algebra will relate to vectors; I tend to use tensor notation as it seems to be more intuitive and can do most linear algebra and more. — Quondumtc 19:44, 17 December 2011 (UTC)
- Honestly I think even that task sounds beyond me right now :) What I really need is a review of all fundamental operations in linear algebra, in "traditional" fashion side by side with "GA fashion". Then I would need to do the same thing for vector calculus. Maybe at /Basic GA? Ideally I would do some homework problems of this sort, to refamiliarize myself with how all this works. I can't imagine tackling something like Dirac's equation when I don't even fully grasp the form or meaning of Maxwell's equations and Einstein's equations. Rschwieb (talk) 14:05, 17 December 2011 (UTC)
One more thing I've been forgetting to tell you. There's a "rotation" section in the GA article, but no projection or reflection mentioned yet... Think you could insert these sections above Rotations? Rschwieb (talk) 17:12, 20 December 2011 (UTC)
- Sure, I'll put something in, and then we can panelbeat it. Have you had a chance to decide whether my "simplistic (but rigorous)" on GA basics approach is worth using? — Quondumtc 21:20, 20 December 2011 (UTC)
- Sorry, I haven't had a chance to look at it yet. I've got a lot of stuff to do between now and February so it might be a while. Feel free to work on other projects in the meantime :) Rschwieb (talk) 13:17, 21 December 2011 (UTC)
Direction of Geometric algebra article[edit]
Update: I noticed the Projections section the fundamental identity is used to rewrite am-1 as the sum of dot and wedge. Is there a fast way to explain why this identity should hold for inverses of vectors? Rschwieb (talk) 13:17, 21 December 2011 (UTC)
- Facepalm* of course their inverses are just scalar multiples :) I've never dealt with an algebra where units were so easy to find! Rschwieb (talk) 14:51, 21 December 2011 (UTC)
- Heh-heh. I had expected objections other than that, but I'm not saying which... — Quondumtc 15:15, 21 December 2011 (UTC)
- Well, I'm not handy with the nuts and bolts yet. Another thing I was going to propose is that Geometric calculus can probably fill its own page. We should get a userspace draft going. That would help make the GA article more compact. Rschwieb (talk) 15:23, 21 December 2011 (UTC)
- It makes sense that a separate Geometric calculus page would be worthwhile, and that it should be linked to as the main article. What is currently in the article is very short, and probably would not be made much more compact, but should remain as a thumbnail of the main article. I think the existing disambiguation page should simply be replaced: it is not necessary. — Quondumtc 16:27, 21 December 2011 (UTC)
- I know what's there now is nice, but consider that it might be better just to have a sentence or two about what GC accomplishes and a Main template to the GC article. To me this seems like the best of all worlds, contentwise. Rschwieb (talk) 16:42, 21 December 2011 (UTC)
- Now you're talking to the purist in me. This is exactly how I feel it should be: with the absolute minimum of duplication. Developing computer source code for maintainability hones this principle to a discipline. There is a strong tendency amongst some to go in the opposite direction, and an even higher principle is that we all need to find a consensus, so I usually don't push my own ideal. — Quondumtc 08:31, 22 December 2011 (UTC)
- I know what's there now is nice, but consider that it might be better just to have a sentence or two about what GC accomplishes and a Main template to the GC article. To me this seems like the best of all worlds, contentwise. Rschwieb (talk) 16:42, 21 December 2011 (UTC)
- It makes sense that a separate Geometric calculus page would be worthwhile, and that it should be linked to as the main article. What is currently in the article is very short, and probably would not be made much more compact, but should remain as a thumbnail of the main article. I think the existing disambiguation page should simply be replaced: it is not necessary. — Quondumtc 16:27, 21 December 2011 (UTC)
- Well, I'm not handy with the nuts and bolts yet. Another thing I was going to propose is that Geometric calculus can probably fill its own page. We should get a userspace draft going. That would help make the GA article more compact. Rschwieb (talk) 15:23, 21 December 2011 (UTC)
On one hand, I do appreciate economy (as in proofs). On the other hand, as a teacher, I also have to encourage my students to use standard notation and to "write what they mean". If I don't do that then they inevitably descend into confusion because what they have written is nonsense and they can't see their way out. At times like that, extra writing is worth the cost. Here in a WP article though, when elaboration is a click away, we have some flexibility to minimize extra text. Some people do print this material :) Rschwieb (talk) 13:08, 22 December 2011 (UTC)
- A complete sidetrack, but related: I found these interesting snippets by Lounesto, and though they might interest you: [4], [5], [6]. — Quondum☏✎ 09:55, 24 January 2012 (UTC)
Defining "abelian ring"[edit]
Extended content
|
|---|
|
The article section Idempotence#Idempotent ring elements defines an abelian ring as "A ring in which all idempotents are central". Corroboration can be found, e.g. here. Since this is a variation on the other meanings associated with abelian, it seems this should be defined, either in a section in Ring (mathematics) or in its own article Abelian ring. It seems more common to define an abelian ring as a ring in which the multiplication operation is commutative, so this competing definition should be mentioned too. Your feeling? — Quondum☏✎ 09:14, 21 January 2012 (UTC)
Err... – what am I missing? Surely if abelian ring is not notable enough for (ii) or (iii), then it would not be notable enough for (i)? — Quondum☏✎ 19:19, 24 January 2012 (UTC)
|
The two idempotents being central only comes into play for the ring decomposition, and I think I can convince you where they come from. If R is the direct sum of two rings, say A and B, then obviously the identity elements of A and B are each central idempotents in R, and the ordered pair with the two identities is the identity of R! Conversely if R can be written as the direct sum of ideals A and B, then the identity of R has a unique representation as a+b=1 of elements in those rings. It's easy to see that A and B are ideals of R, and by definition of the decomposition A∩B=0. I'll leave you to prove that a and b are central idempotents and that a is the identity of A and b is the identity of B. Rschwieb (talk) 23:31, 27 January 2012 (UTC)
- Yes, it's kinda obvious when you put it like that. I think I'm getting the feel of an ideal, though this is not necessary to understand the argument, depending on what definition of "direct sum" you use. The "uniqueness" of my left- and right- decompositions seems pretty pointless. The proof you "leave to me" seems so simple that I'm worried I'm using circular arguments. When I originally saw a while back that a subring does not need the same identity element as the ring, I was taken aback. I like the decomposition into prime ideals. In particle physics, spinors (particles) seem to decompose in such a way into "left-handed" and "right-handed" "circular polarizations". — Quondum☏✎ 06:59, 28 January 2012 (UTC)
- Decomposition: the Krull Schmidt theorem is the most basic version of what algebraists expect to happen. I can see that the unfamiliarity with direct sum is making it harder to understand, so I'll try to sum it up. Expressing a module as a direct sum basically splits it into neat pieces. The KST says that certain modules can be split into unsplittable pieces, and another such factorization must have factors isomorphic to the first one, in some order.
- Ideals: Here is how I would try to help a students sort them out. I think we've already discussed that modules are just "vector spaces" over rings other than fields, and you are forced to distinguish between multiplication on the left and right since R doesn't have to be commutative. Just like you can think of a field as a vector space over itself, you can think of a ring as being a module over itself. However, F only has two subspaces (the trivial ones) but a ring may have more right submodules (right subspaces) than just the trivial ones. These are exactly the right ideals.
- From another point of view, I'm sure you've seen right ideals described as additive subgroups of R which "absorb" multiplication by ring elements on the right, and ideals absorb on both sides. This is a bit different from fields, which again, only have trivial ideals. Even matrix rings over fields only have trivial two-sided ideals (although they have many many onesided ideals).
- The next thing I find helpful is the analogy of normal subgroups being the kernels of group homomorphisms. Ideals of R are exactly the kernels of ring homomorphisms from R to other rings. Right ideals are precisely the kernels of module homomorphisms from R to other modules. These two types of homomorphisms are of course completely different right? A module homomorphism doesn't have to satisfy f(xy)=f(x)f(y), and a ring homomorphism doesn't have to satisfy f(xr)=f(x)r.
- Finally in connection with the last point, it's important to know that forming the quotient R/A, while it is always of course a quotient of groups, needs special conditions on A to be anything more. If A is a right ideal, then R/A is a right R module. If A is an ideal, then R/A is a ring. If A has no absorption properties, then R/A may have no special structure beyond being a group. Rschwieb (talk) 15:01, 28 January 2012 (UTC)
Tensor calculus in physics? (instead of GA)[edit]
(Moved this discussion to User talk:Rschwieb/Physics notes.)
Happy that you moved all that to somewhere more useful. =)
FYI, you might link your subpage User:Rschwieb/Physics notes to my sandbox User:F=q(E+v^B)/sandbox. It will be a summary of the most fundamental, absolutely core, essential principles of physics (right now havn't had much chance to finish it):
- the fundamental laws of Classical mechanics (CM), Statistical mechanics (SM), QM, EM, GR, and
- a summary of the dynamical variables in each formalism; CM - vectors (fields), EM - scalars/vectors (fields), GR - 4-vectors/tensors (fields), QM - operators (mostly linear), and
- some attempt made at scratching the surface of the theory at giddy heights way way up there: Relativistic QM (RQM) (from which QFT, QCD, QED, Electroweak theory, the particle physics Standard model etc. follows).
- postulates of QM and GR,
- intrinsic physical concepts: GR - reference frames and Lorentz transformations, non-Euclidean (hyperbolic) spacetime, invariance, simultaneity, QM - commutations between quantum operators and uncertainty relations, Fourier transform symmetry in wavefunctions (although mathematical identities, still important and interesting)
- symmetries and conservation
- general concepts of state, phase, configeration spaces
- some attributes of chaos theory, and how it arises in these theories
There may be errors that need clarification or correction, don't rely on it too heavily right now.
Feel free to remove this notice after linking, if so. =) Best wishes, F = q(E+v×B) ⇄ ∑ici 21:04, 1 April 2012 (UTC)
- It looks like a nice cheatsheet/study guide. Thanks for alerting me to it! I would not even know of the existence of half of these things, so it's good to have them all in one spot when I eventually come to read about them.
- The goal of my physics page is to be a source of pithy statements to motivate the material. I think physicists and engineers have more of these on hand than I do! Rschwieb (talk) 13:47, 2 April 2012 (UTC)
- That’s very nice of you to say! I promise it will be more than just a cheat sheet though (not taken as an insult! it does currently look lousy). F = q(E+v×B) ⇄ ∑ici 17:52, 2 April 2012 (UTC)
rings in matrix multiplication[edit]
Hi, you seem to be an expert in mathematical ring theory. Recently I have been re-writing matrix multiplication because the article was atrocious for its importance. Still the term "ring" is dotted all over the article anyway, maybe you could check its used correctly (instead of "field"? Although they appear to be some type of set satisfying axioms, like a group, field, or vector space, I haven’t a clue what they are in detail, and all these appear to be so similar anyway...). In particular here under "Scalar multiplication is defined:"
- "where λ is a scalar (for the second identity to hold, λ must belong to the centre of the ground ring — this condition is automatically satisfied if the ground ring is commutative, in particular, for matrices over a field)."
what does "belong to the centre of the ground ring" mean? Could you somehow re-word this and/or provide relevant links (if any) for the reader? ("Commutative" has an obvious meaning). Thank you... F = q(E+v×B) ⇄ ∑ici 14:21, 8 April 2012 (UTC)
- OK, I'll take a look at it. You can just think of rings as fields that don't have inverses for all nonzero elements, and don't have to have commutative multiplication. I think I know what the author had in mind in the section you are looking at. Rschwieb (talk) 15:06, 8 April 2012 (UTC)
- Thanks for your edits. Although there doesn't seem to be any link to "ground ring"... I can live with it. It’s just that the reader would be better served if one existed. At least you re-worded the text and linked "centre". F = q(E+v×B) ⇄ ∑ici 17:17, 8 April 2012 (UTC)
- "Ground ring" just means "ring where the coefficients come from". I couldn't think of a link for that, but maybe it should be introduced earlier in the article. Rschwieb (talk) 17:31, 8 April 2012 (UTC)
- It's not too obvious where to introduce it (a little restructuring is still needed to allow this). The idea is that the elements of the matrix and the multiplying scalars can all be elements of any chosen ring (the ground ring, though I'm not familiar with the term). F, if you are not sure of any details, I'm happy to help too if you wish; I just don't want to get in the way of any rewrite. — Quondum☏ 19:00, 8 April 2012 (UTC)
- Thanks for your edits. Although there doesn't seem to be any link to "ground ring"... I can live with it. It’s just that the reader would be better served if one existed. At least you re-worded the text and linked "centre". F = q(E+v×B) ⇄ ∑ici 17:17, 8 April 2012 (UTC)
- I didn't realize the response, sorry (not on the watchlist... it will be added). No need to worry about the re-write, its pretty much done and you should feel free to edit anyway. =)
- IMO wouldn't it be easier to just state the matrix elements are "numbers or expressions", since most people will grip that easier than the term "elements of a ring" every now and then (even though technically necessary), and perhaps describe the properties of matrix products in terms of rings in a separate (sub)section? Well, it's better if you two decide on how to tweak any bits the reader can't easily access or understand... (not sure about you two, but the terminology is really odd: can understand the names "set, group, vector space", but "ring, ground ring, torsonal ring..."? strange names...)
- In any case, thanks to both of you for helping. =) F = q(E+v×B) ⇄ ∑ici 19:55, 9 April 2012 (UTC)
- You make a good point. There is a choice to be made: the article should either describe matrix multiplication in familiar terms and follow this with a more abstract section generalizing it to rings as the scalars, or else it should introduce the concepts of a ring, a centre, a ground ring, etc., then define the matrix multiplication in terms of this. I think that while the second approach may appeal to mathematicians familiar with the concepts of abstract algebra, the bulk of target audience for this article would not be mathematicians, making the first approach more appropriate. — Quondum☏ 20:16, 9 April 2012 (UTC)
- Agreed with the former (separate, abstract explanations in its own section, keeping the general definition as familiar as possible). Even with just numbers (integers!), matrix multiplication is quite a lot to take in for anyone (at a first read, of course trivial with practice...). That’s without using the abstract terminology and definitions. Definitions through abstract algebra would probably switch off even scientists/engineers who know enough maths for calculations but not pure mathematical theory, never mind a lay reader... F = q(E+v×B) ⇄ ∑ici 20:26, 9 April 2012 (UTC)
Examples[edit]
Sorry for the late response and then taking extraordinarily long to produce fairly low quality examples anyway... =( I'll just keep updating this section every now and then... Please do feel free to ask about/critisise them. F = q(E+v×B) ⇄ ∑ici 16:27, 13 April 2012 (UTC)
- Thanks for anything you produce along these lines. I had never seen the agenda of physics laid out like you did on your page, and I think I'm going to learn a lot from it. All the physics classes I took were just trees in the forest but never the forest. Rschwieb (talk) 18:17, 13 April 2012 (UTC)
A barnstar for you![edit]
Possible geometric interpretation of tensors?[edit]
Hi, recently yourself, F=q(E+v^B), and Quondum, and me briefly talked about tensors and geometry. Also noticed you said here "indices obfuscate the geometry" (couldn't agree more). I have been longing to "draw a tensor" to make clear the geometric interpretation, it’s easy to draw a vector and vector field, but a tensor? Taking the first step, is this a correct possible geometric diagram of a vector transformed by a dyadic to another vector, i.e. if one arrow is a vector, then two arrows for a dyadic (for each pair of directions corresponding to each basis of those directions)? In a geometric context the number of indices corresponds to the number of directions associated with the transformation? (i.e. vectors only need one index for each basis direction, but the dyadics need two - to map the initial basis vectors to final)?
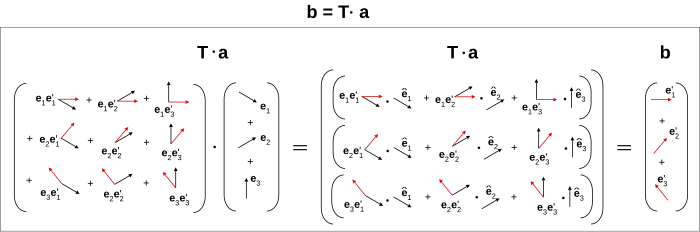
Analagously for a triadic, would three indices correspond to three directions (etc. up to n order tensors)? Thanks very much for your response, I'm busy but will check every now and then. If this is correct it may be added to the dyadic article. Feel free to criticize wherever I'm wrong. Best, Maschen (talk) 22:29, 27 April 2012 (UTC)
- First of all, I want to say that I like it and it is interesting, but I don't think it would go well in the article. I think it's a little too original for an encyclopedia. But don't let this cramp your style for pursuing the angle! Rschwieb (talk) 01:42, 28 April 2012 (UTC)
- Ok, I'll not add it to any article, the main intent is to get the interpretation right. Is this actually the right way of "drawing a dyadic", as a set of two-arrow components, or not? Also the reason for picking on dyadics is because the are several 2nd order tensors in physics, which have this geometric idea: usually in the tensor is a property of the material/object in question, and is related to the directional response of one quantity to another, such as
an applied to a material/object of results in in the material/object, given by angular velocity ω moment of inertia I an angular momentum L electric field E Electrical conductivity σ a current density flow J electric field E polarizability α (related is the permittivity ε, Electric susceptibility χE) an induced polarization field P
- (obviously there are many more examples) all of which have a similar directional relations to the above diagram (except usually both basis are the standard Cartesian type). Anyway thanks for an encouraging response. I'll also not distract you with this (inessential) favour, I just hope we can both again geometric insight to tensors, and the connection between indices and directions (btw - its not the number of dimensions that concerns me, only directions, in that tensors seem to geometrically be multidirectional quantities). Maschen (talk) 07:11, 28 April 2012 (UTC)
- Just to warn you, I think you'll find both my geometric sense and my physical sense severely disappointing
 That said, I will find it pleasant to ponder such thoughts, in an attempt to improving both of those senses. Rschwieb (talk) 21:27, 28 April 2012 (UTC)
That said, I will find it pleasant to ponder such thoughts, in an attempt to improving both of those senses. Rschwieb (talk) 21:27, 28 April 2012 (UTC)
- Just to warn you, I think you'll find both my geometric sense and my physical sense severely disappointing
- If I may comment, I suspect some geometric insight may be obtained via a geometric algebra interpretation. Keeping in mind that correspondence is only loose, a dyadic or 2nd-order tensor corresponds roughly with a bivector rather than a pair of vectors, even though an ordered pair of vectors specifies a simple dyadic. There are fewer degrees of freedom in the simple dyadic than in an ordered pair of vectors. So I'd suggest that a dyadic is better interpreted as an oriented 2D disc than two vectors, and a triadic as an oriented 3D element rather than as three vectors etc., but again this is not complete (a dyadic has more dimensions of freedom than an oriented disc has, and thus is more "general": the geometric elements described correspond rigorously to the fully antisymmetric part of a dyadic, triadic etc.). In general, a dyadic can represent a general linear mapping of a vector onto a vector, including dilation (differentially in orthogonal directions) and rotations. Geometrically this is a little difficult to draw component-wise. — Quondum☏ 22:12, 28 April 2012 (UTC)
- Thanks Quondum, I geuss this highlights the problem with my understanding... dyadics, bivectors, 2nd order tensors, linear transformations... seem loosely similar with subtleties I'm not completely familiar with inside out. The oriented disc concept seems to be logical, but what does the oriented disk correspond to? The transformation from one vector to another? (this is such an itchy for me question because I always have to draw things before understanding them, even if its just arrows and shapes...) Maschen (talk) 13:05, 29 April 2012 (UTC)
- The oriented disc is not a good representation of a general linear transformation (too few degrees of freedom, for one) except in the limited sense of a rotation, but is a more directly geometric concept in the way a vector is. It has magnitude (area) and orientation (including direction around its edge, making it signed), but no specific shape; it is an example of something that can be depicted geometrically. Examples include an oriented parallelogram defined by two edge vectors, torque and angular momentum: pretty much anything you'd calculate conventionally using the cross product of two true vectors. If you want to go into detail it may make sense to continue on your talk page to avoid cluttering Rschwieb's. I'm watching it, so will pick up if you post a question there; you can also attract my attention more immediately on my talk page. — Quondum☏ 16:42, 29 April 2012 (UTC)
- Ok. Thanks/apologies Quondum and Rschwieb, I don't have much more to ask for now. Quondum, feel free to remove my talk page from your watchlist (not active), I may ask on yours in the future... Maschen (talk) 05:28, 30 April 2012 (UTC)
- The oriented disc is not a good representation of a general linear transformation (too few degrees of freedom, for one) except in the limited sense of a rotation, but is a more directly geometric concept in the way a vector is. It has magnitude (area) and orientation (including direction around its edge, making it signed), but no specific shape; it is an example of something that can be depicted geometrically. Examples include an oriented parallelogram defined by two edge vectors, torque and angular momentum: pretty much anything you'd calculate conventionally using the cross product of two true vectors. If you want to go into detail it may make sense to continue on your talk page to avoid cluttering Rschwieb's. I'm watching it, so will pick up if you post a question there; you can also attract my attention more immediately on my talk page. — Quondum☏ 16:42, 29 April 2012 (UTC)
Your question of User talk:D.Lazard[edit]
I have answered there.
Sincerely D.Lazard (talk) 14:56, 2 June 2012 (UTC)
Aplogies and redemption...[edit]
sort of, for not updating Mathematical summary of physics recently. On the other hand I just expanded Analytical mechanics to be a summary style article. If you have use for this, I hope it will be helpful. (As you may be able to tell, I tend to concentrate on fundamentals rather than examples). =| F = q(E+v×B)⇄ ∑ici 01:56, 22 June 2012 (UTC)
Intolerable behaviour by new user:Hublolly[edit]
Hello. This message is being sent to inform you that there is currently a discussion at WP:ANI regarding the intolerable behaviour by new user:Hublolly. The thread is Intolerable behaviour by new user:Hublolly. Thank you.
See talk:ricci calculus#The wedge product returns... for what I mean (I had to include you by WP:ANI guidelines, sorry...)
F = q(E+v×B)⇄ ∑ici 23:04, 9 July 2012 (UTC)
- Fuck this - User:F=q(E+v^B) and user:Maschen are both thick-dumbasses (not the opposite: thinking smart-asses) and there are probably loads more "editors" like these becuase as I have said thousands of times - they and their edits have fucked up the physics and maths pages leaving a trail of shit for professionals to clean up. Why that way???
- What intruges me Rschwieb is that you have a PHD in maths and yet seem to STILL not know very much when asked??? that worries me, hope you don't end up like F and M.
- I will hold off editing untill this heat has calmed down. Hublolly (talk) 00:16, 10 July 2012 (UTC)
- Hublolly - according to my tutors even if one has a PHD it still takes several years (10? maybe 15?) before you have proficiency in the subject and can answer anything on the dot. It’s really bad that YOU screwed up every page you have edited, then come along to throw insult to Rschwieb who has a near-infinite amount of knowledge on hard-core mathematical abstractions (which is NOT the easy side of maths) compared to Maschen, me, and yes - even the "invincible you", and given that Rschwieb is a very good-faith, productive, and constructive editor and certainly prepared to engage in discussions to share thoughts on the subject with like-minded people (the opposite of yourself). F = q(E+v×B)⇄ ∑ici 00:30, 10 July 2012 (UTC)
- I DIDN'T intend to persionally attack Rschwieb. Hublolly (talk) 08:32, 10 July 2012 (UTC)
I demand that you apologize after calling me a troll (or labelled my behaviour "trollish") on your buddy's talk page, given that I just said I didn't personally attack you. :-(
I also request immediatley that you explicitly clarify your post at "WP:ANI" because I have no idea what this means - do you?
This isn't going away. Hublolly (talk) 13:41, 10 July 2012 (UTC)
- Hublolly - it will vanish. Rschwieb has no reason to answer your dum questions: he didn't "call you a troll" (he did say your behaviour was like trolling) and you already know what you have been doing. What comments about you from others do you to expect, after all you have done??? F = q(E+v×B)⇄ ∑ici 16:03, 10 July 2012 (UTC)
- @Hublolly There is nothing to discuss here. Cease and desist from cluttering my talkpage any further in this way. Only post again if you have constructive ideas for a specific article. Thank you. Rschwieb (talk) 12:06, 11 July 2012 (UTC)
Your message from March2012[edit]
Hello, you left this message for me back in March: "Hi, I just noticed your comment on the Math Desk: "This is the peril of coming into maths from a physics/engineering background - not so hot on rings, fields etc..." I am currently facing the reverse problem, knowing all about the rings/fields but trying to develop physical intuition :) Drop me a line anytime if there is something we can discuss. Rschwieb (talk) 18:39, 26 March 2012 (UTC)" - I'm really sorry, this must be the first time I've logged into my account since then - I normally browse without logging in. Thank you saying hello, if anything comes up I'll certainly message you - Chris Christopherlumb (talk) 11:57, 22 July 2012 (UTC)
- That's OK, when dropping comments like that I prepare myself for long waits for responses :) Everything from my last post still holds true! Rschwieb (talk) 15:41, 23 July 2012 (UTC)
Hom(X)[edit]
The reference to Fraleigh that I inserted into the Endomorphism ring article uses Hom(X) for the set of homomorphisms of an abelian group X into itself. This is also consistent with notation used for homomorphisms of rings and vector spaces in other texts. Since this is simply an alternate notation, I recommend that it be in the article. — Anita5192 (talk) 18:17, 24 July 2012 (UTC)
- The contention is that it must not be very common. If you can cite two more texts then I'll let it be. Rschwieb (talk) 18:51, 24 July 2012 (UTC)
- Okay, you win. I could not find Fraleigh's notation anywhere else. I was thinking of the notation Hom(V,W) for two separate algebraic structures. Nonetheless, I think Fraleigh is an excellent algebra text. I have summarized the results of my search in Talk:Endomorphism ring. — Anita5192 (talk) 04:36, 27 July 2012 (UTC)
The old question of a general definition of orthogonality[edit]
We once discussed the general concept of orthogonality in vector spaces and rings briefly (or at least I think so: I failed to find where). We identified the apparently irreconcilable examples of vectors (using bilinear forms) and idempotents of a ring (using the ring multiplication), and you suggested that it may be defined with respect to any multiplication operator. I think I've synthesized a generally applicable definition that comfortably encompasses all these (vindicating and extending your statement), and may directly generalise to modules. The concepts of left and right orthogonality with respect to a bilinear form appear to be established in the literature.
My definition of orthogonality replaces bilinear forms with bilinear maps:
- Given any bilinear map B : U × V → W, u ∈ U and v ∈ V are respectively left orthogonal and right orthogonal to the other with respect to B if B(u,v) = 0W, and simply orthogonal if u is both left and right orthogonal to v.
I would be interested in knowing whether you have run into something along these lines before. — Quondum☏ 02:47, 11 August 2012 (UTC)
- Nope! Can't say I have an extensive knowledge of orthogonality. I think the ring theoretic analogue is just that, and I'm not sure if it was really meant to be clumped with the phenomenon you mention. The multiplication operation of an algebra is certainly additive and k bilinear, though. I'm still merrily on my way through the Road to Reality. Reading about bundles now, where he is doing a good job. I couldn't grasp much about what he said about tensors... and the graphical notation he uses really doesn't inspire me that much. Maybe some cognitive misconceptions are hindering me... Rschwieb (talk) 00:40, 12 August 2012 (UTC)
- It may not have been intended to be clumped together, but it seems to be a natural generalization that includes both. My next step is to try to identify the most suitable bilinear map for use in defining orthogonality between any pair of blades (considered as representations of subspaces of the 1-vector space) in a GA in a geometrically meaningful way, and hopefully from there for elements of higher rank (i.e. non-blades) too – as a diversion/dream. Bundles I'm not strong on, so Penrose didn't make much of an impression on me there. Tensors I feel reasonably comfortable with, so don't remember many issues. I'm with you on Penrose graphical notation: I think it is a clumsy way of achieving exactly what his abstract index notation does far more elegantly and efficiently, and has no real value aside from as a teaching tool to emphasise the abstractness of the indices, or perhaps for those who think better using more graphic tools. I don't think you're missing anything – it is simply what you said: uninspiring. There is, however, a very direct equivalence between the abstract and the graphical notations, and the very abstractness of the indices must be understood as though they are merely labels to identify connections: you cannot express non-tensor expressions in these notations, unlike the notation of Ricci calculus. Penrose also does a poor job of Grassman and Clifford algebras. Happy reading! — Quondum☏ 01:19, 12 August 2012 (UTC)
I saw this EoM link being added to Bilinear map. It really does seem to generalize bilinearity and orthogonality to the max, beyond my own attempts. However, it also seems to neglect another generalization to modules covered in Bilinear map. In any event, my own generalization has been vindicated and exceeded, though reconciling these two apparently incompatible definitions of bilinearity on modules may be educational. — Quondum 08:54, 22 January 2013 (UTC)
- Cool. Thanks! Rschwieb (talk) 14:45, 22 January 2013 (UTC)
Sorry (about explaining accelerating frames incorrectly)...[edit]

Remember this question you asked?
I was not thinking clearly back then when I said this:
- "About planet Earth: locally, since we cannot notice the rotating effects of the planet, we can say locally a patch of Earth is an inertial frame. But globally, because the Earth has mass (source of gravitational field) and is rotating (centripetal force), then in the same frame we chose before, to some level of precision, the effects of the slightly different directions of acceleration become apparent: the Earth is obviously a non-uniform mass distribution, so gravitational and centripetal forces (of what you refer to as "Earth-dwellers" - anything on the surface of the planet experiances a centripetial force due to the rotation of the planet, in addition to the gravitational acceleration) are not collinearly directed towards the centre of the Earth, also there are the perturbations of gravitational attraction from nearby planets, stars and the Moon. These accelerations pile up, so measurements with a spring balance or accelerometer would record a non-zero reading."
This is completely wrong!! Everywhere on Earth we are in an accelerated frame because of the mass-energy of the Earth as the source of local gravitation. Here is the famous thought experiment (Equivalence principle, see pic right from general relativity):
- Someone in a lab on Earth (performing experiments to test physical laws) accelerating at g is equivalent to someone in a rocketship (performing experiments to test physical laws) accelerating at g. Both observers will agree on the same results.
You may have realized the correct answer by now and that I mislead you. Sorry about that, and hope this clarifies things. Best. Maschen (talk) 21:55, 25 August 2012 (UTC)
- That's OK, I think I eventually got the accurate picture. If you know where that page is, then you can check the last couple of my posts to see if my current thinking is correct :) It's OK if you occasionally tell me wrong things... I almost never accept explanations without question unless they're exceedingly clear! I'm glad you contributed to that conversation. Rschwieb (talk) 01:11, 26 August 2012 (UTC)
some GA articles[edit]
Hi Rschwieb. I noticed you have made some recent contributions related to geometric algebra in physics. You may be interested in editing gauge theory gravity or Riemann–Silberstein vector if you are familiar with the topics. Teply (talk) 07:00, 3 September 2012 (UTC)
About Covariance and contravariance of vectors...[edit]
Hi. A while back you said Hernlund's drawing was not as comprehensible as it could be (..... IMO first ever brilliant image of the concept I have seen).....
Do you think the new svg version I drew back then (although only recently added to the article) is clearer? Just concerned for people who have difficulty with geometric concepts (which includes yourself?), since WP should make these things clear to everyone.
I have left a note on Hernlund's talk page btw. Thanks, Maschen (talk) 19:49, 3 September 2012 (UTC)
- Yeah: as I recall, didn't it used to be all black and white? That would have made it especially confusing. I guess I could never make sense of the picture. If you could post here what the "vital" things to notice are, then maybe I could begin to appreciate it. These might even be really simple things. I think the red and yellow vectors are clear, but I just have no feeling for the blue vectors. If you need to talk about all three types to explain it to me, then by all means go ahead! Rschwieb (talk) 13:28, 4 September 2012 (UTC)
- One of the nonessential things is the coordinate background. The coordinates are only related to the basis in the illustrated way in a holonomic basis. the diagram would illustrate the concept better without it, using only an origin, but the basis and cobasis would have to be added.
- The yellow vectors are the components of the red vector in terms of the basis {ei}. The blue vectors are the components of the red vector in terms of the cobasis {ei}. Here I am using the term components in the true sense of vectors that sum, not the typical meaning of scalar coefficients. The cobasis, in this example, is simply another basis, since we have identified the vector space with its dual via a metric. Aside from the summing of components, the thing to note is that every cobasis element is orthogonal to every basis element except for the dual pairs that, when dotted, yield 1. — Quondum 13:59, 4 September 2012 (UTC)
- PS: How does this work for you?: A basis is used to build up a vector using scalar multipliers (old hat to you). The cobasis is used to find those scalar multipliers from the vector (and dually, the other way round). The diagram illustrates the vector building process both ways. (It could do with parallelograms to show the vector summing relationship.) — Quondum 14:12, 4 September 2012 (UTC)
- The crucial thing was to differ between the covariant and contravariant vectors, and provide the geometric interpretation. I disagree that the coordinates are "non-essential" (for diagrammatic purposes), since its much easier to imagine vectors tangent to coordinate curves or normal to coordinate surfaces, when faced with an arbitrary coordinate system one may have to use. How is it possible to show diagrammatically the tangent (basis) and normal (cobasis) vectors without some coordinate-based construction? With only an origin, they would just look like any two random bases used to represent the same vector (which is an important fact that any basis can be used, but this isn't the purpose of the figure). Do you agree, Rschwieb and Quondum?
- Adding extra lines for the parallelogram sum seems like a good idea, anything else?
- The basis and cobasis are stated all over the place in the article, in particular here in the article, in Hernlund's drawing, and in my own drawing at the top (the basis/cobasis are labelled). Maschen (talk) 15:39, 4 September 2012 (UTC)
- The vectors tangent to the intersection of coordinate surfaces and perpendicular to a coordinate surface can be illustrated can be done with planes spanned by basis vectors, all in a vector space without curvilinear surfaces. And the point of co- and contravariance is precisely that it applies to arbitrary ("random") bases, and it applies without reference to any differential structure. Nevertheless, I do not feel strongly about this point. Perhaps the arrow heads could be made a little narrower? (They tend to fool the eye into thinking the paraellelogram summation is inexact). Most of my explanation was aimed at Rschwieb, to gauge the reaction of someone who feels less familiar with this, not as comment on the diagram. — Quondum 20:52, 4 September 2012 (UTC)
- Hmm, I understand what you're saying, but would still prefer to keep the coordinates for reasons above, also mainly to preserve the originality of Hernlund's design. The arrowheads are another good point. Let's wait for Rschwieb's opinions on modifications. In any case Quondum thanks so far for pointing out very obvious things I didn't even think about (!)... Maschen (talk) 21:43, 4 September 2012 (UTC)
- Feel free to experiement! It's going to be some time before I can absorb any of this... Rschwieb (talk) 12:54, 5 September 2012 (UTC)
- But is there anything you would like to suggest to improve the diagram, Rschwieb!? Maschen (talk) 13:03, 5 September 2012 (UTC)
- Feel free to experiement! It's going to be some time before I can absorb any of this... Rschwieb (talk) 12:54, 5 September 2012 (UTC)
- Hmm, I understand what you're saying, but would still prefer to keep the coordinates for reasons above, also mainly to preserve the originality of Hernlund's design. The arrowheads are another good point. Let's wait for Rschwieb's opinions on modifications. In any case Quondum thanks so far for pointing out very obvious things I didn't even think about (!)... Maschen (talk) 21:43, 4 September 2012 (UTC)
That the usual basis vectors lie in the tangent plane is one of the few concrete things I can hold onto, so I'd say I rather like seeing the curved surface in the background (but maybe some extraneous labeling could be reduced?) Even if this picture acturately graphs the dual basis with respect to this basis, I still have no feeling for it. Algebraically it's very clear to me what the dual basis does: it projects onto a single coordinate. But physically, I have no feeling what that means, and I don't know how to interpret it in the diagram. To me the space and the dual space are two different disjoint spaces. I know that the inner product furnishes a bridge (identification) between the two of these, but I have not developed sense for that either at this point. I'm guessing it's via this bridge that you can juxtapose the vectors and their duals right next to each other.
Q: I appreciate that you can see the basis and dual basis for what they are independently of the "manifold setting". I'll keep it in mind as I think about it that the manifold may just be a distraction. Is there any way you could develop a few worked examples with randomly/strategically chosen bases, whose dual base description is particularly enlightening? Rschwieb (talk) 15:44, 5 September 2012 (UTC)
- So.. you're basically saying to keep the coordinate curves and surfaces? I'll just add the parallelogram lines in and reduce the arrowhead sizes.
- For background: It's really not hard to visualize the dual basis = cobasis = basis 1-forms = basis covectors ... (too many names!! just listing for completeness). They are vectors normal to the coord surfaces, or more accurately (as far as I know) stacks of surfaces (which automatically possess a perpendicular sense of direction to the surfaces).
- Think of the "basis vector duality" reducing to "tangent" (to coord curves) and "normal" (to coord surfaces) , that's essentially the geometry, I'm sure you know the geometric interpretations of these partial derivatives and nabla. Maschen (talk) 16:34, 5 September 2012 (UTC)
- My sense for anything outside of regular Euclidean vector algebra is rudimentary. I do not have a good feel for tensor notation or geometry, yet. I did run across something like what you said in the Road to Reality. Something about rather than picturing a covector as a vector, you think of it as the plane perpendicular to the base of the vector. Maybe you can elaborate? Rschwieb (talk) 17:07, 5 September 2012 (UTC)
- This diagram is best understood in terms of Euclidean vectors: as flat space with curvilinear coordinates. Does this help? — Quondum 17:16, 5 September 2012 (UTC)
- I cannot picture what might be meant by the perpendicular planes. The perpendicular places correspond to the Hodge dual, but that is not really the duality we are looking at, or at least I don't see the connection. If you give me a page reference, perhaps I could check? — Quondum 17:33, 5 September 2012 (UTC)
- Found it: §12.3 p.225. I'll need time to interpret this. — Quondum 17:47, 5 September 2012 (UTC)
- Okay, here's my interpretation. A covector can be represented by the vectors in its null space (i.e. that it maps to zero) and a scale factor for parallel planes. So this (n−1)-plane in V is associated with each covector in V∗, with separate magnitude information. The dual basis planes defined in this way each contain n−1 of the basis vectors. The action of the covector is to map vectors that touch spaced parallel planes to scalar values, with the not-contained basis vector touching the plane mapped to unity. Within the vector space V, there is no perpendicularity concept: only parallelism (a.k.a. linear dependence). All this makes sense without a metric tensor. Whew! — Quondum 18:19, 5 September 2012 (UTC)
- This diagram is best understood in terms of Euclidean vectors: as flat space with curvilinear coordinates. Sorry, I'm not sure that it does. I understand that the manifold isn't necessary, and I may as well just think of a vector space with vectors pointing out of the origin as I always do. However, when I'm asked to put the dual basis in that picture too, I find that I really can't see how they would fit. For me, you see, they exist in a different vector space. I remember that the inner product furnishes some sort of natural way to bridge the space V with its dual, and I suspect that's the identification you are both making when viewing the vectors and their duals in the same space.(?)
- My sense for anything outside of regular Euclidean vector algebra is rudimentary. I do not have a good feel for tensor notation or geometry, yet. I did run across something like what you said in the Road to Reality. Something about rather than picturing a covector as a vector, you think of it as the plane perpendicular to the base of the vector. Maybe you can elaborate? Rschwieb (talk) 17:07, 5 September 2012 (UTC)
- I also need to reread parts of Road to Reality again. I'm only doing a once-over now. I am very curious about what goes on differently between vector and "covector" fields. Rschwieb (talk) 20:42, 5 September 2012 (UTC)
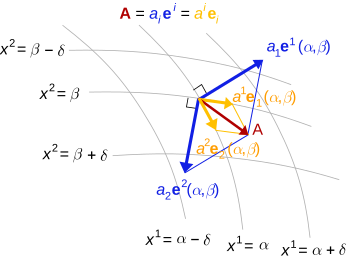
You may have been thinking of the other form of the (Hodge?) dual, in relation to the orthogonal complement of an n-plane element in N-dimensional space (1 ≤ n ≤ N)? That's not what I meant previously. Everything I'm talking about is in flat Euclidean space, but still in curvilinear coordinates.
About the covectors in the Hernlund diagram:
- The coordinates are curvilinear in 2d.
- Generally - the coord surfaces are regions where one coordinate is constant, all others vary (you knew that, just to clarify in the diagram's context)...
- In the 2d plane: the "coordinate surfaces" degenerate to just 1d curves, since for x1 = constant there is a curve of x2 points, and vice versa.
- Generally - coordinate curves are regions where one coordinate varies and all others are constant (again you knew that).
- In the 2d plane: the coordinate curves are obvious in the diagram, though happen to coincide with the surfaces in this 2d example... x1 = constant "surface" is the x2 coord curve, and vice versa, so in 2d the "coordinate curves" are again 1d curves.
- So, the cobasis vectors (blue) are normal to the coordinate surfaces. The basis vectors (yellow) are tangent to the curves. For the Hernlund example, that's all there is to the geometric interpretation...
- In 3d, coord surfaces would be 2d surfaces and coord curves would be 1d curves.
About "stacks of surfaces" in the Hernlund diagram:
- Just think of any x1 = constant = c, then keep adding α (which can be arbitrarily small, it's instructive and helpful to think it is), i.e. x1 = c, c + α, c + 2α ... this (or of course x2 = another constant, and keep adding another small increment β)
- The normal direction to the surfaces is the maximum rate of change of intersecting the surfaces, any other direction has a lower rate.
- The change in xi for i = 1, 2 is: dxi = ∇xi•dr, where of course r = (x1, x2).
- This is the reason that "dxi" is used in differential form notation, and has the geometric interpretation as a stack of surfaces, with the "sense" in the normal direction to the surfaces.
- From the Hernlund diagram, the surface stack x1 = c, c + α, c + 2α ... for small α with its sense in the direction of the blue arrows corresponds to the basis 1-form. But it seems equivalent to just use the blue arrows for the basis 1-forms = cobasis...
About the inner product as the "bridge":
Interestingly, according to Gravitation (book), considering a vector a as an arrow, and a 1-form Ω as a stack of surfaces,
if the arrow a is run through the surface stack Ω, the number of surfaces pierced is equal to the inner product <a, Ω >:
Correct me if wrong, but all this is as I understand it. Hope this clarifies things from my part. Thanks, Maschen (talk) 21:32, 5 September 2012 (UTC)
Summary of above Geometry/Algebra Covariance Contravariance Nomenclature of "vector" vector, contravariant vector covector, 1-form, covariant vector, dual vector Basis is... tangent normal ...to coordinate curves surfaces ...in which one coord varies, all others are constant. one coord is constant, all others vary. The coordinate vector transformation is... while the basis transformation is... ...which are invariant since: The inner product is:
- where L is the transformation from one coord system (unbarred) to another (barred). I do not intend to patronize you nor induce excessive explanatory repetition, but writing this table helped me also (this was adapted from what I wrote at talk:Ricci calculus (Proposal?...)) ... Maschen (talk) 21:56, 5 September 2012 (UTC)
- R, it seems we need to ensure that there are no lurking misconceptions at the root. As M has confirmed, we are talking about euclidean space in this diagram, and you need not consider curved manifolds; the coordinate curves have simply been arbitrarily (subject to differentiability) drawn on a flat sheet. In the argument about covectors-as-planes, we are dealing purely with a vector space, and have dropped any metric. The rest of the argument happens in the tangent space of the manifold (which is a vector space, whereas the manifold is an affine space), with basis vectors determined by the tangents to the coordinate curves. The simpler (but nevertheless complete) approach is simply to ignore the manifold, and start at the point of the arbitrary basis vectors in a vector space. (From here think in 3 D, to distinguish planes from vectors.) The picture of the covector "as" planes of vectors is precisely a way of visualising the action of a covector wholly within the vector space (as a parameterised family of parallel subsets) without referring to the dual space, and without using any concept of a metric. You can skew the whole space (i.e. apply any nondegenerate linear mapping to every vector in the space), and make not one iota of difference to the result. I think that you may be expecting it to be more complex than it is. — Quondum 05:08, 6 September 2012 (UTC)
- Most of category theory is "abstract nonsense", but the notion of functor is a bit easier. From the article: "Dual vector space: The map which assigns to every vector space its dual space and to every linear map its dual or transpose is a contravariant functor from the category of all vector spaces over a fixed field to itself." Maybe that helps someone? Also, the image above contains some obvious errors for upper/lower indices. Teply (talk) 07:38, 6 September 2012 (UTC)
- Abstractions (like category theory and functors, as you say) will help Rschwieb and Quondum (which is good thing!), but just to warn you - not if you're like me who (1) has to draw a picture of everything even when it can't be done (in particular tensors and spinors), (2) can't comprehend absolute pure mathematical abstractions properly (only a mixture of maths/physics). Although were looking for geometric interpretations. I'll fix the image (the components are mixed up as you say, my fault). Thanks for your comments though Teply (of course work throughout WP). Maschen (talk) 11:34, 6 September 2012 (UTC)
Thanks, Teply, for the functor connection. This is definitely something I want to take a look at.
M: I think I'm going to ignore the background manifold for now, as Q suggests. As I understand it, the curvilinear coordinates just furnish the "instantaneous basis" at every point, but that does not really directly bear on my questions about the dual basis.
Q: I think you hit upon one of my misconceptions. All of those vectors are in the tangent space? When I saw the diagram, I mistook them to be nearly normal to the tangent space! That might be a potential thing to address about the diagram.(?)
M+Q: (As always, I really appreciate the detailed answers, but please bear in mind that with my current workload it takes me a lot of time to familiarize myself with it. Still, I don't want to simply stop responding until the weekend. I hope I can phrase short questions and inspire a few short answers to help me digest the contents you two authored.) M mentioned that the dual basis vectors are "orthogonal" to some of the original basis, and that's through the "bilinear pairing" that you get by making the "evaluation inner product" . This might be the appropriate bridge I was thinking of. This is present even in the absence of an inner product on V. I *think* that when an inner product is present, the bilinear pairing between V and V* is somehow strengthened to an identification. I was thinking that this identification allowed us to think of vectors and covectors as coexisting in the same space. Rschwieb (talk) 14:40, 6 September 2012 (UTC)
- Yup, all those vectors are in the tangent space at the point of the manifold shown as their origin. This is a weak point of this kind of diagram, and would bear pointing out in the caption. Every basis covector is "orthogonal" to all but one basis vector. (I assume you are referring to V∗×V→K as a bilinear pairing. I'd avoid the notation ⟨⋅,⋅⟩ for this.) And yes, when an "inner product" ⟨⋅,⋅⟩ (correctly termed a symmetric bilinear form in this context) is used for the purpose, it allows us to identify vectors with covectors (because given u∈V∗, there is a unique x∈V such that u(⋅)=⟨x,⋅⟩ and vice versa), and we then do generally think of them as being in the same space, even if it is "really" two spaces with a bijective mapping. — Quondum 16:40, 6 September 2012 (UTC)
- It may make life easier if I stay out of this for a while (and refrain from cluttering Rschwieb's talk page). If there are any modifications anyone has to propose, just list them here (I'm watching) or on my talk page and I'll take care of the diagram. Thanks for this very stimulating and interesting and discussion, bye for now... Maschen (talk) 16:47, 6 September 2012 (UTC)
School Project[edit]
Hey there- I am doing a school project on Wikipedia and Sockpuppets. Do you mind giving your personal opinions on the following questions?
1. Why do you think people use sockpuppets/vandalise on Wikipedia?
2.How does it make you feel when you see a page vandalised?
3. What do you think is going through the mind of a sock puppeteer?
Thank you! --Ice Cream is really tasty (talk) 12:42, 19 September 2012 (UTC)
- Hi there! That sounds like a pretty good school project, actually :)
- 1) I can imagine there are hundreds of unrelated reasons, so this is a pretty deep question! First of all, there are probably people out there who actually want to damage what is in articles, but I think it's pretty hard to understand their motives, and they are already pretty strange people. The vast majority of vandals (+socks) do what they do for another reason, that is, they think it's funny. This can range from actual humor that's just mischevous (like changing "was a famous mathematician" to "was a famous moustachematican" if the guy has a funny moustache) to much more serious vandalism. I said they think it's funny because I really don't think the more serious vandal/sock behavior which is disruptive and offensive is actually funny. For some of these people, it is funny to "be a person who spoils things". You can probably find a book on vandalism which explains that aspect better than I can. The best I can guess is they "like the attention" that they think they get from the action.
- 2) It was a little obnoxious at first, but now that I've seen a wide spectrum of the dumb stuff vandals do, it's not so bad. I've found that there are far more people who correct things than spoil things, and in most cases vandalism is up only momentarily. The really dumb vandals can even be counteracted by computer programs.
- 3) Let's talk about two breeds of sockpuppeteers. The first type is easy to understand: they just want to inflate their importance by making it look like a lot of people agree with them. The second type, the type that just wants to cause chaos (this is a type of vandalism), is harder to understand. I don't think I can offer much help understanding the second type. I guess that the chaos sockpuppeteers take abnormal enjoyment in "being a spoiler" and "having people's attention". Wasting your time makes their day, for some reason.
- Hope this helps, and good luck on your project. Rschwieb (talk) 13:08, 19 September 2012 (UTC)
- Sadly, the OP is a socking troll. Tijfo098 (talk) 19:04, 19 September 2012 (UTC)
- That's too bad (and half expected) :) Still, it is a good school project idea, and I'm keeping this to point people to if they have the same question! Rschwieb (talk) 19:56, 19 September 2012 (UTC)
- Sadly, the OP is a socking troll. Tijfo098 (talk) 19:04, 19 September 2012 (UTC)
Hi[edit]
-> User talk:YohanN7/Representation theory of the Lorentz group#Discussions from Rschwieb's talk page
Hello,
I was intensionally that I have suppressed the case of local rings: IMO, it adds only the equivalence of projectivity and freeness in this case, which is not the subject of the article. But if you think it should be left, I'll not object. D.Lazard (talk) 22:56, 26 October 2012 (UTC)
- Hmm, well it's not a case, I think you still must be being bewildered by what used to be there! The case is that "local ring (without noetherian) makes f.g. flats free". I think that is just as nice as the "noetherian ring makes f.g. flats projective." Rschwieb (talk) 00:18, 27 October 2012 (UTC)
- Sorry, I missed the non Noetherian case. D.Lazard (talk) 08:24, 27 October 2012 (UTC)
TeX superscripts[edit]
It was a "lexing error" because that's the message I got when I tried to use it. I've used it before without a problem, but when I typed I got a lexing error. Then I tried Failed to parse (syntax error): {\displaystyle a^{-1}</math and got a "lexing error". If you can tell me how to fix this, I'd appreciate it. Wait, I have an idea. Maybe <math>a^-^1} . Nope, that didn't work either. Rick Norwood (talk) 18:34, 12 November 2012 (UTC)
I visited the article and now I understand your comment. If it was I who removed that caret, I apologize. Thanks for catching it and fixing it. Rick Norwood (talk) 18:48, 12 November 2012 (UTC)
- Well the incurred typo was a problem too, but I really was interested in why you altered in in other places too.
- displays fine for me, and it would for you too in the above paragraph if you put another > next to your </math. Rschwieb (talk) 18:50, 12 November 2012 (UTC)
Thanks. I'll fix it in the article. Rick Norwood (talk) 19:04, 12 November 2012 (UTC)
I'm still having trouble. I'll try copy and paste of your version above. Rick Norwood (talk) 19:09, 12 November 2012 (UTC)
- You might see help:displaying a formula. Use curly brackets to group everything in the subscript as Rschwieb has done:
a^{-1}. Maschen (talk) 19:12, 12 November 2012 (UTC)
Well, that worked, though I'm still baffled why it didn't work before (even when I didn't forget the close wedge bracket). Thanks to Maschen for the link to help. Rick Norwood (talk) 19:15, 12 November 2012 (UTC)
- Every once in a while the math rendering goes wiggy. I'm glad to hear it worked out. Rschwieb (talk) 19:31, 12 November 2012 (UTC)
Algebras induced on dual vector spaces[edit]
Given the dual G∗ of a vector space G (over ℝ), we have the action of a dual vector on a vector: ⋅ : G∗ × G → ℝ (by definition), and we can choose a basis for G and can determine the reciprocal basis of G∗. Do you know of any results relating further algebraic structure on the vector space, to structure on the dual vector space? An obvious relation is ℝ-bilinearity of the action: (αw)⋅v=w⋅(αv)=α(w⋅v) and distributivity. A bilinear form on G seems to directly induce a bilinear form on G∗. Given additional structure such as a bilinear product ∘ : G × G → G or related structure, are you aware of induced relations on the action or an induced operation in the dual vector space? — Quondum 15:39, 26 November 2012 (UTC)
- I think you might find this link useful. Search "dual space." in the search field. I can spout a few things off the top of my head that I'm not confident about. I think the dual space and the second dual should always have the same dimension (even for infinite dimensions.) All three are always isomorphic, but the better thing to have is natural isomorphisms. The original space is always naturally isomorphic to its second dual, but not to its first dual. If the vector space has an inner product, then there is a natural isomorphism to the first dual. (I'm unsure if finite dimensionality matters here.)
- I don't think I can give you a satisfactory answer about how bilinear forms on G relate to those on G*. If G has an inner product, I'm tempted to belive they are identical, but otherwise I have no idea. Rschwieb (talk) 18:25, 26 November 2012 (UTC)
- Thanks. Lots there for me to go through before I come up for breath again. It seems to have a lot on duality, seems to go into exterior algebra extensively as well, and seems pretty readable to boot. At a glance, it seems to be pretty thorough/rigorous; just what I need, even if it might not give me all the answers that I want on a plate. — Quondum 09:29, 27 November 2012 (UTC)
- After some cogitation I have come up with the proposition that there is no "further structure" induced for a nondegenerate real Clifford algebra (regarded as a ℝ-vector space and a ring), aside from a natural the decomposition into the scalar and non-scalar subspaces, and from this the scalar product (defined in the GA article); not even the exterior product. With one curious exception: in exactly three dimensions, there is a natural decomposition into four subspaces, corresponding to the grades of the exterior algebra. I'm not too sure what use this is, but at least it has elevated my regard for the scalar projection operator and the scalar product as being "natural". — Quondum 08:38, 7 December 2012 (UTC)
- Thanks. Lots there for me to go through before I come up for breath again. It seems to have a lot on duality, seems to go into exterior algebra extensively as well, and seems pretty readable to boot. At a glance, it seems to be pretty thorough/rigorous; just what I need, even if it might not give me all the answers that I want on a plate. — Quondum 09:29, 27 November 2012 (UTC)
Jacobson's division ring problem[edit]
Hint (a): Consider the expression t of the form t = ysy–1 – xsx–1, with x and y related. As you would have assumed from the symbols, take s ∈ S and x,y ∈ D ∖ S.
You'll need some trial-and-error, so this may still be frustrating. The next hint (b) will give the relationship between x and y. — Quondum 05:17, 31 December 2012 (UTC)
- Erck. I see the proof of the Cartan–Brauer–Hua theorem on math.SE is taken almost straight from Paul M. Cohn, Algebra, p. 344. Horrible: mine is much prettier. I've seen another as well, complicated in that it uses another theorem. Seeing as mine does not appear to be the standard proof, I think you'll appreciate its elegance more if you let me give you clue (c) first – which, after all, is barely more than I've already given you. — Quondum 11:07, 1 January 2013 (UTC)
- That is Cohn's proof, really? Then the poster is less honest than he appears (or just lucky) :) After this is all over, I'll certainly be looking to see how Lam presented it. Anyhow, I could definitely use that hint (I tried several things for y but had no luck. To me it seemed unlikely that I'd be able to invert anything of the form a+b, so I mainly was focused on products of x,s and their inverses as candidates for y.) Rschwieb (talk) 14:26, 2 January 2013 (UTC)
- Think again: you don't have to invert it; just cancel it. (b) y = x + 1. (c) Then consider the expression ty, substitute t and y and simplify. Consider what you're left with. You should be able to slot your before and after observations into what I've said on my page (2012-12-17T20:37) to produce the whole proof without further trouble. — Quondum 18:14, 2 January 2013 (UTC)
- Thanks, I got it with that hint :) This approach is very simple. As I examine Lam's exercises, it looks like you have rediscovered Brauer's proof :) That's something to be proud of! I can't believe I didn't try x+1... but it goes to show me that when I write off stuff too early, I can close doors on myself. (This happens in chess, too.)
- I see what you meant about the proofs given in Lam's lesson being more eomplicated. I think this is because he is drawing an analogy with the "Lie" version he gives earlier. Brauer's approach appears in the exercises. If you don't have access to that whole chapter, I might be able to obtain copies for you. Lam is typically an excellent expositor, so I think you'd enjoy it. Rschwieb (talk) 15:09, 11 January 2013 (UTC)
- No, Lam's proof is simple, essentially the same as mine: (13.17) referring to (13.13). Various other authors have unnecessarily complicated proofs. I only have access to a Google preview. Thanks for the accolade, but I'm not too sure how much of it is warranted. All I did was to consider a given proof too clunky, and I progressively reworked it, stripping out superfluous complexity while preserving the chain of logic.
- I see that I still haven't managed to bait you with the generalization. So far, I think it might generalize to rings without (nonzero) zero-divisors instead of division rings, in which a set U of units exists that generates the ring via addition and where U−1 are also units, an example being Hurwitz quaternions. I'm having a little difficulty with the intersection lemma, but if it holds, this would be a neat and particularly powerful generalization. — Quondum 18:39, 11 January 2013 (UTC)
- Think again: you don't have to invert it; just cancel it. (b) y = x + 1. (c) Then consider the expression ty, substitute t and y and simplify. Consider what you're left with. You should be able to slot your before and after observations into what I've said on my page (2012-12-17T20:37) to produce the whole proof without further trouble. — Quondum 18:14, 2 January 2013 (UTC)
I remember you had mentioned generalization, but at the time I didn't see what part generalizes. All elements being invertible played a very prominent role in the proof. Which steps are you thinking can be generalized? Faith and Lam hint at a few generalizations, but I think they are pretty limited. Rschwieb (talk) 19:27, 11 January 2013 (UTC)
- I assume that you have the proof that I emailed to you. I would like to generalize it by replacing the division ring requirement with an absence of zero divisors, and the stabilization by the entire group of units by the existence of a set of units that satisfies two requirements: generation the ring through addition and producing units when 1 is subtracted. I see only the intersection lemma as a possible weak point. — Quondum 21:26, 11 January 2013 (UTC)
- Here is an interesting article. I haven't verified it, but I'm guessing it's fine. It has a simple proof of the theorem where D is can be replaced with any ring extension L of (the division ring) S. (That would only entail, as you might expect, that S is a unital subring of L, and that's all!). That seems to beat generalization along the dimension of D to death. Now, of course, one wonders how much we can alter S's nature. Rschwieb (talk) 22:03, 11 January 2013 (UTC)
- Yes, very nice, and it probably goes further than I intended, except in the direction of generalizing S. It requires stabilization ∀d∈D:dS⊆Sd, which is prettier and more general than dSd−1⊆S (I had this in mind as a possibility: it does not rely on units). Perhaps we can replace S as a division ring with a zero-divisor-free ring, or better? I will need to look at this proof for a while to actually understand it. BTW: "S is a unital subring of L" → "S is a division subring of L", surely? — Quondum 07:01, 12 January 2013 (UTC)
- Yes: I meant to emphasize "the (division ring) S as a unital subring of L."
- I think the first baby-step to understanding changes to S is this: Can S be just any subring of D? The answer to this is probably "no". Since I know you don't need distractions at the moment, you might sit back and let me look for counterexamples. Let me know when the pressure is off again! Rschwieb (talk) 15:50, 12 January 2013 (UTC)
- Yes, very nice, and it probably goes further than I intended, except in the direction of generalizing S. It requires stabilization ∀d∈D:dS⊆Sd, which is prettier and more general than dSd−1⊆S (I had this in mind as a possibility: it does not rely on units). Perhaps we can replace S as a division ring with a zero-divisor-free ring, or better? I will need to look at this proof for a while to actually understand it. BTW: "S is a unital subring of L" → "S is a division subring of L", surely? — Quondum 07:01, 12 January 2013 (UTC)
- Here is an interesting article. I haven't verified it, but I'm guessing it's fine. It has a simple proof of the theorem where D is can be replaced with any ring extension L of (the division ring) S. (That would only entail, as you might expect, that S is a unital subring of L, and that's all!). That seems to beat generalization along the dimension of D to death. Now, of course, one wonders how much we can alter S's nature. Rschwieb (talk) 22:03, 11 January 2013 (UTC)
Helping someone with quaternions[edit]
Do you think you could help this guy? I am trying to get you involved on math.SE. Rschwieb (talk) 15:10, 11 January 2013 (UTC)
- Who's "you"? You're on your own page here. I posted a partial answer on math.SE (but am unfamiliar with the required style/guidelines): higher-level problem solving required. Give me a few months before prodding me too hard in this direction; my plate is rather full at the moment (contracted project overdue, international relocation about to happen...). — Quondum 16:21, 11 January 2013 (UTC)
- Ah! Forgot I was on my own talkpage :) OK, thanks for the update. Rschwieb (talk) 17:27, 11 January 2013 (UTC)
Disambiguation link notification for January 12[edit]
Hi. Thank you for your recent edits. Wikipedia appreciates your help. We noticed though that when you edited Torsion (algebra), you added a link pointing to the disambiguation page Regular element (check to confirm | fix with Dab solver). Such links are almost always unintended, since a disambiguation page is merely a list of "Did you mean..." article titles. Read the FAQ • Join us at the DPL WikiProject.
It's OK to remove this message. Also, to stop receiving these messages, follow these opt-out instructions. Thanks, DPL bot (talk) 11:52, 12 January 2013 (UTC)
Create template: Clifford algebra?[edit]
Hi! I know you have extensive knowledge in this area, so thought to ask: do you think this is a good idea to integrate such articles together? It could include articles on GA, APS, STA, and spinors; there doesn't seem to be a template:spinor, recently I may have overloaded the template:tensors with spinor-related/-biased links, although there is a Template:Algebra of Physical Space. I'm not sure if this has been discussed before (and haven’t had much chance to look..). Thanks, M∧Ŝc2ħεИτlk 22:05, 31 January 2013 (UTC)
Lorentz reps[edit]
Hi R!
Now a substantial part of what I wrote some time ago has found its place in Representation theory of the Lorentz group. So, the highly appreciated effort you and Q put in by helping me wasn't completely in vain.
Some of the mathematical parts that have not (yet) gone into any article can go pretty much unaltered into existing articles, particularly into bispinor. I am preparing the ground for it now. If I get the time, other mathematical parts might go into a separate article, describing an alternative formalism, based entirely of tensor products (and suitable quotients) of SL(2;C) reps. This formalism is used just as much as the one in the present article.
The physics part might also become something. Who knows? What I do know is that is an identified need (for instance here and here to be precise) for an overview article making this particular description (no classical field, no Lagrangian) of QFT. It's a monstrous undertaking so it will have to wait. Cheers! YohanN7 (talk) 21:29, 22 February 2013 (UTC)
Reply at Lie bracket[edit]
Hi, I left a reply for you at Talk:Lie_bracket_of_vector_fields#unexplained_notation_in_Properties_section. Cheers, AxelBoldt (talk) 19:00, 20 April 2013 (UTC)
Muphrid from math stack exchange[edit]
Hi Rschwieb, was there something you wanted to discuss? Muphrid15 (talk) 16:47, 16 May 2013 (UTC)
- Hello! Firstly, because of our common interest of Clifford algebras, I was just hoping to attract your attention to the little group that works on here. Because of your solutions at m.SE, I thought your input would be valuable, if you offered it from time to time. There's no pressure, just a casual invitation.
- Secondly, we were just coming off of this question. Honestly it looks a little crankish to me. Too florid: too metaphysical. He lost my attention when he said: Am I on to something here? If we could build a Clifford algebra multiplication device with laser beams on a light table, would that not reveal the true nature of Clifford algebra? And in the process, reveal something interesting about how our mind works?. Without commenting there, I just wanted to communicate that we might do better ignoring this guy.
- Anyhow, glad to have a second point of contact with you. If you contribute to the math pages here, I hope you find the editors helpful. Rschwieb (talk) 17:15, 16 May 2013 (UTC)
- Yeah, for sure. Ages ago I wrote a section on rotations with GA rotors, but I think that was too much of a soupy mess of math than anything anyone could've appreciated, at the time. A CA/GA group around here is exciting to me, and I'll be keeping an eye on what's going on and how I might be able to chip in.
- As far as that person on m.se, yeah, just a bit off in space there. What I like about GA is how we start with this algebra and it doesn't inherently mean anything--it isn't until we start attaching geometric significance to the elements of the algebra that we get a powerful formalism for doing problems in that regime. But talking about that and the human brain? Goodness gracious. Thanks for the invitation! Muphrid15 (talk) 17:50, 16 May 2013 (UTC)
- I think GA has a little "crank magnetism" due to its underdog status. Fortunately, there is plenty of substance to using it, and interest from big names. That bodes well for its survival. Anyway, glad to have you here! Let me know if I can be of any help... Rschwieb (talk) 13:04, 17 May 2013 (UTC)
Fractionalization[edit]
Not to distract you from sprucing up the GA page (or life itself), but out of interest for something a bit different...
Do you happen to have experience and resources on fractional calculus applied to differential geometry? Namely fractional form spaces, fractional exterior derivatives, fractional exterior covariant derivatives, etc? Or even a fractional geometric calculus? There is a plentiful literature on the fractional calculus even with physical applications but so little on fractional differential forms etc, which is a shame since it looks so fascinating... I wish I had the time and expertise to write these WP articles, recently drafted this (hardly much of a draft) where a few papers can be found. Anyway thanks.
Before you mention it, indeed it would be better to upgrade the present GA and geometric calculus articles before any fractionalization... M∧Ŝc2ħεИτlk 19:20, 20 May 2013 (UTC)
- Nope... I've never heard of fractional calculus, and I barely have any understanding of differential geometry, so I wouldn't be of much help. I've heard of "taking the square root of an operator" before, though. It struck me that it was probably well studied in operator theory, but the wiki page does not seem to support that idea. Beyond Hadamard, I didn't recognize any of the names in the references as "big names." But naturally, my lack of recognition might just be a sign of my unfamiliarity with the field :) Good luck! Rschwieb (talk) 10:34, 21 May 2013 (UTC)
- Absolutely not one encounter of FC?... No matter, thanks anyway!! It's entirely inessential for now anyway: even if the articles could be created, the literature is apparently so scrimp they would be nuked by "lack-of-source" or "POV" deletionists!
- It doesn't matter..... but another thing I forgot to ask concerning "fractionalization" was the possibility of describing fractals using GA, which easily accounts for all natural number dimensions. (Fractals have non-integer dimensions greater than their topological dimension - not just rational- but transcendental-valued in general). I.e, between a 2d bivector and 3d trivector would be an infinite continuum of subspaces, all the real number dimensions between 2 and 3, like the surface of a crumpled sheet of paper or leaf etc. Integration would replace summation over k-blades for k ∈ ℝ.
- Is there any way? (I asked a couple of Dr's and a Prof at uni a few months back - they said they haven't encountered any... and asked at the WP ref desk with the conclusion that there probably isn't). These things are fun to speculate about IMO. Best, M∧Ŝc2ħεИτlk 23:30, 21 May 2013 (UTC)
- I think you are forgetting how new I am to GA :) While I can pick up the algebra rather quickly, I still know almost nothing about the calculus, because I'm really rusty at multidimensional calculus (and rather ignorant of differential geometry.) I do look forward to seeing what develops from this idea :) Rschwieb (talk) 13:36, 22 May 2013 (UTC)
- @Maschen: Fractional calculus appears to work with fractional powers of operators over a differential manifold. As such, it does not seek to change the domain of the operators, being fields over these manifolds. The way I see your objective, there would be no call for modifying the underlying GA to describe fractals etc., only of the operators (e.g. ∇k). To be more concrete, fractals have some measure that scales as a fractional power of scale, but the fractal lives in a space that has a whole number of dimensions. Similarly, fractional calculus is applied over a discrete number of variables. A corollary is that a GA with blades of a fractional number of dimensions is an unrelated exercise either to fractals or to fractional calculus. What Rschwieb may be able to back me up on is that the idea of extending a real CA to work on a fractional number of dimensions probably just does not make sense, or at least will be an unexplored area of immense complexity. Fractional exponentiation (with a real exponent) may be possible in a GA, but with difficulties due to the problem of choosing a princple branch of the function (see Exponentiation to get a flavour for a GA over one a 1-d vector space, also known as complex or hyperbolic numbers). However, this does not lead to k-blades with reak k as you describe. So, while GA applied to fractional calculus and fractals probably makes sense, relating these to fractional-k blades probably doesn't. — Quondum 18:40, 22 May 2013 (UTC)
- I think you are forgetting how new I am to GA :) While I can pick up the algebra rather quickly, I still know almost nothing about the calculus, because I'm really rusty at multidimensional calculus (and rather ignorant of differential geometry.) I do look forward to seeing what develops from this idea :) Rschwieb (talk) 13:36, 22 May 2013 (UTC)
- Is there any way? (I asked a couple of Dr's and a Prof at uni a few months back - they said they haven't encountered any... and asked at the WP ref desk with the conclusion that there probably isn't). These things are fun to speculate about IMO. Best, M∧Ŝc2ħεИτlk 23:30, 21 May 2013 (UTC)
- Well the speculation is likely to be wrong and misguided. (And forbidden by WP:talk page guideline gabble anyway). Concerning your (Quondum) edit summary, I am not stating that fractional calculus integrated into GA would describe fractals - I meant the two things (fractals in GA and FC in GA) separately. I have more to say but simply don't have the time for now. Thanks anyway Rschwieb and Quondum for feedback. M∧Ŝc2ħεИτlk 15:01, 23 May 2013 (UTC)
- For clarity, in my edit summary I meant separation of a fractional basis of GA from the concepts of fractals and a FC in GC. The latter two I took as self-evidently distinct. — Quondum 17:11, 23 May 2013 (UTC)
Premature closing of MathSci's RfE against D.Lazard by Future Perfect at Sunrise?[edit]
I wish to notify you of a discussion that you were involved in.[7] Thanks. A Quest For Knowledge (talk) 15:42, 22 May 2013 (UTC)
Universal group ring property[edit]
A proof with too many details in some places and not enough details in others. One technicality to keep in mind is that these are all finite linear combinations (that's really what "linear combination" means, but it doesn't hurt to emphasize).
Let be a group homomorphism of G into an F algebra A. We claim that there is an algebra homomorphism extending f called . Furthermore, we can prove the map is given by .
Proof: By the universal property of vector spaces, any assignment of a basis of F[G] into another F-vector space extends uniquely to an F-linear map. Clearly f maps a basis of F[G] into the vector space A, and so the universal property of vector spaces grants us that the suggested map is an F-linear transformation. Explicitly, for any x,y in F[G] and alpha, beta in F.
The only things that remain are to show that is multiplicative as well, and sends identity to identity. We compute:
Thus, the extension is multiplicative. It is truly an extension since .
Finally, the identity maps to the identity. First note that the identity of F[G] is just . The multiplicative identity of A is necessarily the identity of the group of units of A, and this identity must be shared by all subgroups, in particular, the image of f. Since f is a group homomorphism, it preserves this identity. Furthermore, . QED
In summary, it was no great surprise that there was a unique linear extension of f. The interesting thing gained was that since f is multiplicative on G, the extension is multiplicative on F[G]. Rschwieb (talk) 13:14, 5 August 2013 (UTC)
Is a torsion-free module over a semihereditary ring flat?[edit]
It's so if the ring is an integral domain (i.e., Prufer domain.) I'm just curious, but also it would be nice to have a discussion of the non-domain case in flat module. -- Taku (talk) 00:20, 6 August 2013 (UTC)
- That's an interesting question, but I'm not sure because there isn't a standard definition of torsion-free for rings outside of domains. Do you have a particular definition in mind?
- Have you been past Torsionless_module yet? If not, check out Chase's theorem as it appears there. That explains the connection between torsionless modules and semihereditary rings once and for all.
- I'm not very knowledgeable about torsionfree/torsionless modules, but I don't think there is a very strong connection between them even for commutative domains. Torsionfree --> torsionless for domains, but the article says Q is not a torsionless Z module (but it is flat hence torsionfree). It just happens that torsionfree=torsionless over Prufer domains, but I don't kno wif it can be dissected into something finer. Hope this is useful! Rschwieb (talk) 13:39, 6 August 2013 (UTC)
- Ah, I see: it's about definitions. But flat module claims "flat" implies "torsion-free" for any commutative ring. So, my question should make sense? The definition at torsion-free module seems like a standard one. If so, flat module should make note that that is indeed the definition used there. I have to look at some texts to familiarize myself with the matter. -- Taku (talk) 15:32, 8 August 2013 (UTC)
- I remember adding to torsionfree and torsionless module articles, and I wonder if I put that in or not. Take a look at Lam's text, page 127. He offers a definition of torsion-freeness that indeed generalizes flatness. For future reference, projective modules are torsionfree, but I'm not sure if flat modules are torsionfree... Rschwieb (talk) 17:03, 8 August 2013 (UTC)
- I think I remember toying with the idea of using Lam's "torsion-free" definition. As much as I like his versions of stuff, I think I decided against it in the end. It is one of few definitions he gives that I can't say I see in other places. The main definition for torsion-free that I see is "if r is a regular element and mr=0 then m=0" and "the annihilator of m in R is an essential right ideal." I don't think either one of these is equivalent to Lam's definition. And 'oh boy' I've been overlooking the definition that already exists at Torsion_free_module. I'm not fluent with Tor so I don't know how it's related to previous stuff I said. Rschwieb (talk) 17:09, 8 August 2013 (UTC)
Banned user suggesting edits[edit]
Mathsci is now posting on his own talk page to suggest edits. I have reported this at Wikipedia:Administrators'_noticeboard#Banned_user_suggesting_edits and thought it proper to mention that you had been receiving messages from him. You will see at that board why I find the situation somehwat unsatisfactory. Deltahedron (talk) 19:31, 9 February 2014 (UTC)
- Now referred to Wikipedia:Arbitration/Requests/Enforcement#Mathsci by another user. Deltahedron (talk) 07:33, 10 February 2014 (UTC)
Response re: gravitomagenetism[edit]
I responded to you on my talk page. Fresheneesz (talk) 21:58, 29 August 2014 (UTC)
Clifford Algebra[edit]
Hi, I have't forgotten that you wanted to discuss a bit further. I'd like that too. I'm on sort of a semi-Wiki-break right now, but, in the meanwhile, could you elaborate on
- By the way, I'm interested in seeing (if you have an example in mind) an illustrative example of leveraging basis elements of a complex space that square to -1. That sounds like an interesting benefit that might normally be passed over in pure math texts.
a bit? I'm not sure exactly what you mean, and there might be no mathematical significance, but there is surely physical significance to be extracted. The complexification is made partly for convenience, partly for the Clifford algebra to actually encompass the physicist convention for the Lie algebra, and partly to encompass transformations that come from O(3, 1), not SO+(3, 1). Actually, not even the full Mn(C) suffices. In order to encompass time reversal, one must have the set of all antilinear transformations as well. These are constructed using simply composition of complex conjugation and an ordinary complex linear transformation. Best! YohanN7 (talk) 20:28, 15 September 2014 (UTC)
One of the first things to note is that under any invertible linear transformation (and in particular Lorentz transformations, but also including a transformation that takes the original real-valued bilinear form with a particular signature to the "standard form") of the underlying vector space, each of the gammas will retain their square, either 1 or −1. Since they retain their square, one might as well (in the physical equations, like the Dirac equation) keep the old gammas in the new frame, because it is their squares that is important. This is part of showing Lorentz invariance of the relativistic equations. There is a little bit of this in Gamma matrices. There is more in a draft for Dirac algebra which you can access from my front page. (Don't hold me responsible for the latter![]() I wrote it quite some time ago, and it is full of bugs and not ready for the actual (quite poor) article.) YohanN7 (talk) 20:48, 15 September 2014 (UTC)
I wrote it quite some time ago, and it is full of bugs and not ready for the actual (quite poor) article.) YohanN7 (talk) 20:48, 15 September 2014 (UTC)
Slightly off topic: The physics of special relativity lies in the Lorentz group. This is either of O(3, 1) or O(1, 3), these two are isomorphic. But the corresponding Clifford algebras are not isomorphic. This is another reason to not single out a real Clifford algebra (and mix in talk about quaternions and stuff in the relevant section of the article). Also, I have read one of Hestenes papers (mentioned by someone on the Clifford algebra talk page or the Spinor article talk page, don't remember) on the Dirac equation couched in a real Clifford algebra. It strikes me as being a somewhat convoluted approach, the "fifth gamma matrix" is defined without the factor i (as is otherwise common practice) and is christened i and works like the imaginary number. YohanN7 (talk) 21:39, 15 September 2014 (UTC)
Ring axioms[edit]
I am intrigued by the claim that the axiom of commutativity of addition in a ring can be omitted – i.e. that it follows from the other ring axioms. In particular, I have not found any flaw, and I do not follow the edit summary in the subsequent revert. Do you have any insight here? —Quondum 20:17, 14 April 2015 (UTC)
- @Quondum : Yes, it's a peculiar fact that the underlying group (of a ring with identity) can be proven to be abelian from the other axioms. Because it *is* a bit of a surprise, and also because rings have a natural categorical description as monoids in the category of abelian groups, ring theorists do not see any merit in thinning out the ring axioms any further. There are a few math.SE posts on this topic that you might enjoy. Here's one, and here's another one. Rschwieb (talk) 12:24, 17 April 2015 (UTC)
- Thanks, that clarifies it for me. I suppose it is the surprise of it that got me. That alone might be worth a footnote relating to redundant axioms in the article. —Quondum 02:55, 18 April 2015 (UTC)
Hi,
You appear to be eligible to vote in the current Arbitration Committee election. The Arbitration Committee is the panel of editors responsible for conducting the Wikipedia arbitration process. It has the authority to enact binding solutions for disputes between editors, primarily related to serious behavioural issues that the community has been unable to resolve. This includes the ability to impose site bans, topic bans, editing restrictions, and other measures needed to maintain our editing environment. The arbitration policy describes the Committee's roles and responsibilities in greater detail. If you wish to participate, you are welcome to review the candidates' statements and submit your choices on the voting page. For the Election committee, MediaWiki message delivery (talk) 13:46, 23 November 2015 (UTC)
I notice that the page you contributed was moved to idempotent (ring theory). The link on your user page to idempotent element now ends up elsewhere, so you may wish to tweak it. —Quondum 19:04, 13 July 2016 (UTC)
Thanks for the heads up :) Not sure I'll undertake any action... feeling a bit lazy about it. Rschwieb (talk) 16:37, 14 July 2016 (UTC)
ArbCom Elections 2016: Voting now open![edit]
Hello, Rschwieb. Voting in the 2016 Arbitration Committee elections is open from Monday, 00:00, 21 November through Sunday, 23:59, 4 December to all unblocked users who have registered an account before Wednesday, 00:00, 28 October 2016 and have made at least 150 mainspace edits before Sunday, 00:00, 1 November 2016.
The Arbitration Committee is the panel of editors responsible for conducting the Wikipedia arbitration process. It has the authority to impose binding solutions to disputes between editors, primarily for serious conduct disputes the community has been unable to resolve. This includes the authority to impose site bans, topic bans, editing restrictions, and other measures needed to maintain our editing environment. The arbitration policy describes the Committee's roles and responsibilities in greater detail.
If you wish to participate in the 2016 election, please review the candidates' statements and submit your choices on the voting page. MediaWiki message delivery (talk) 22:08, 21 November 2016 (UTC)
I tried to cling to the terminology as used in the article besides this pic, and I slightly oppose to your terminology of "rejection normal to the plane".
I prefer to deprecate "rejection" at all, and prefer to talk about projections on orthogonal subspaces, i.e., about projections on the plane and its normal, respectively; and I think that the latter object is no "rejection normal to the plane", but either the mentioned "projection on the normal of the plane", or a "rejection on the plane".
Addendum 06:36, 17 August 2017 (UTC): I truly enjoy Quondum's last edits, introducing different prepositions (onto, from) for the two verbs (project and reject), but maintaining a single object (plane), which is referred to.
In any case, I will not interfere with your edits. Cheers. Purgy (talk) 17:51, 16 August 2017 (UTC)
- Purgy, I'd like to mention that as a general principle, the first place to talk about any specific edit is preferably on the talk page of the article, rather than on the talk page of an editor (unless it does not relate to the content of the edit, such as if the issue is behaviour). This is the kind of thing that benefits from maximum exposure by those who are interested: your initial comment being put there would have invited others to add their perspective. My own edits were simply the result of a literature check, which made it easy :) —Quondum 12:18, 17 August 2017 (UTC)
ArbCom 2019 election voter message[edit]
Definition of zero divisors in Ring (mathematics)[edit]
(Regarding this revert.) With the definition on Zero divisor I see how the original statement makes sense. However, in the paragraph above my edit, zero divisors are defined to be nonzero. Confusingly, there is a footnote on that definition that is inconsistent with regard to that. I suppose one should then remove the 'nonzero' in the definition of zero divisors in Ring (mathematics). What do you think?
Btw: Hope I'm doing this right, it's my first attempt at contributing to Wikipedia :) Framebundle (talk) 20:59, 18 September 2020 (UTC)
- Yes, I think bringing the Ring article in line with the Zero divisor article would be the way to do it with minimal impact. Rschwieb (talk) 17:08, 21 September 2020 (UTC)






















![{\displaystyle {\hat {f)):F[G]\to A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466f6b62abb08cc8b06952a217757c27e49cc6ad)



![{\displaystyle {\hat {f))([\sum _{h}\alpha _{h}h][\sum _{k}\beta _{k}k])={\hat {f))(\sum _{g}(\sum _{hk=g}\alpha _{h}\beta _{k})g)=\sum _{g}(\sum _{hk=g}\alpha _{h}\beta _{k})f(g)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abebf7719ed351bd18d4a5ee19427d973e9da497)

![{\displaystyle =[\sum _{h}\alpha _{h}f(h)][\sum _{k}\beta _{k}f(k)]={\hat {f))(\sum _{h}\alpha _{h}h){\hat {f))(\sum _{k}\beta _{k}k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bae4ed3326418029da87aa4f2168ccaa228b849)


