| Part of a series on |
| Physical cosmology |
|---|
 |
The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time.[1] It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies (which are bound to each other by gravity) recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.
Cosmic expansion is a key feature of Big Bang cosmology. It can be modeled mathematically with the Friedmann–Lemaître–Robertson–Walker metric (FLRW), where it corresponds to an increase in the scale of the spatial part of the universe's spacetime metric tensor (which governs the size and geometry of spacetime). Within this framework, the separation of objects over time is associated with the expansion of space itself. However, this is not a generally covariant description but rather only a choice of coordinates. Contrary to common misconception, it is equally valid to adopt a description in which space does not expand and objects simply move apart while under the influence of their mutual gravity.[2][3][4] Although cosmic expansion is often framed as a consequence of general relativity, it is also predicted by Newtonian gravity.[5][6]
According to inflation theory, during the inflationary epoch about 10−32 of a second after the Big Bang, the universe suddenly expanded, and its volume increased by a factor of at least 1078 (an expansion of distance by a factor of at least 1026 in each of the three dimensions). This would be equivalent to expanding an object 1 nanometer across (10−9 m, about half the width of a molecule of DNA) to one approximately 10.6 light-years across (about 1017 m, or 62 trillion miles). Cosmic expansion subsequently decelerated to much slower rates, until around 9.8 billion years after the Big Bang (4 billion years ago) it began to gradually expand more quickly, and is still doing so. Physicists have postulated the existence of dark energy, appearing as a cosmological constant in the simplest gravitational models, as a way to explain this late-time acceleration. According to the simplest extrapolation of the currently favored cosmological model, the Lambda-CDM model, this acceleration becomes dominant in the future.
History
[edit]In 1912–1914, Vesto M. Slipher discovered that light from remote galaxies was redshifted,[7][8] a phenomenon later interpreted as galaxies receding from the Earth. In 1922, Alexander Friedmann used the Einstein field equations to provide theoretical evidence that the universe is expanding.[9]
Swedish astronomer Knut Lundmark was the first person to find observational evidence for expansion, in 1924. According to Ian Steer of the NASA/IPAC Extragalactic Database of Galaxy Distances, "Lundmark's extragalactic distance estimates were far more accurate than Hubble's, consistent with an expansion rate (Hubble constant) that was within 1% of the best measurements today."[10]
In 1927, Georges Lemaître independently reached a similar conclusion to Friedmann on a theoretical basis, and also presented observational evidence for a linear relationship between distance to galaxies and their recessional velocity.[11] Edwin Hubble observationally confirmed Lundmark's and Lemaître's findings in 1929.[12] Assuming the cosmological principle, these findings would imply that all galaxies are moving away from each other.
Astronomer Walter Baade recalculated the size of the known universe in the 1940s, doubling the previous calculation made by Hubble in 1929.[13][14][15] He announced this finding to considerable astonishment at the 1952 meeting of the International Astronomical Union in Rome. For most of the second half of the 20th century, the value of the Hubble constant was estimated to be between 50 and 90 km⋅s−1⋅Mpc−1.
On 13 January 1994, NASA formally announced a completion of its repairs related to the main mirror of the Hubble Space Telescope, allowing for sharper images and, consequently, more accurate analyses of its observations.[16] Shortly after the repairs were made, Wendy Freedman's 1994 Key Project analyzed the recession velocity of M100 from the core of the Virgo Cluster, offering a Hubble constant measurement of 80±17 km⋅s−1⋅Mpc−1.[17] Later the same year, Adam Riess et al. used an empirical method of visual-band light-curve shapes to more finely estimate the luminosity of Type Ia supernovae. This further minimized the systematic measurement errors of the Hubble constant, to 67±7 km⋅s−1⋅Mpc−1. Reiss's measurements on the recession velocity of the nearby Virgo Cluster more closely agree with subsequent and independent analyses of Cepheid variable calibrations of Type Ia supernova, which estimates a Hubble constant of 73±7 km⋅s−1⋅Mpc−1.[18] In 2003, David Spergel's analysis of the cosmic microwave background during the first year observations of the Wilkinson Microwave Anisotropy Probe satellite (WMAP) further agreed with the estimated expansion rates for local galaxies, 72±5 km⋅s−1⋅Mpc−1.[19]
Structure of cosmic expansion
[edit]The universe at the largest scales is observed to be homogeneous (the same everywhere) and isotropic (the same in all directions), consistent with the cosmological principle. These constraints demand that any expansion of the universe accord with Hubble's law, in which objects recede from each observer with velocities proportional to their positions with respect to that observer. That is, recession velocities scale with (observer-centered) positions according to
where the Hubble rate quantifies the rate of expansion. is a function of cosmic time.
Dynamics of cosmic expansion
[edit]
The expansion of the universe can be understood as a consequence of an initial impulse (possibly due to inflation), which sent the contents of the universe flying apart. The mutual gravitational attraction of the matter and radiation within the universe gradually slows this expansion over time, but expansion nevertheless continues due to momentum left over from the initial impulse. Also, certain exotic relativistic fluids, such as dark energy and inflation, exert gravitational repulsion in the cosmological context, which accelerates the expansion of the universe. A cosmological constant also has this effect.
Mathematically, the expansion of the universe is quantified by the scale factor, , which is proportional to the average separation between objects, such as galaxies. The scale factor is a function of time and is conventionally set to be at the present time. Because the universe is expanding, is smaller in the past and larger in the future. Extrapolating back in time with certain cosmological models will yield a moment when the scale factor was zero; our current understanding of cosmology sets this time at 13.787 ± 0.020 billion years ago. If the universe continues to expand forever, the scale factor will approach infinity in the future. It is also possible in principle for the universe to stop expanding and begin to contract, which corresponds to the scale factor decreasing in time.
The scale factor is a parameter of the FLRW metric, and its time evolution is governed by the Friedmann equations. The second Friedmann equation,
shows how the contents of the universe influence its expansion rate. Here, is the gravitational constant, is the energy density within the universe, is the pressure, is the speed of light, and is the cosmological constant. A positive energy density leads to deceleration of the expansion, , and a positive pressure further decelerates expansion. On the other hand, sufficiently negative pressure with leads to accelerated expansion, and the cosmological constant also accelerates expansion. Nonrelativistic matter is essentially pressureless, with , while a gas of ultrarelativistic particles (such as a photon gas) has positive pressure . Negative-pressure fluids, like dark energy, are not experimentally confirmed, but the existence of dark energy is inferred from astronomical observations.
Distances in the expanding universe
[edit]Comoving coordinates
[edit]In an expanding universe, it is often useful to study the evolution of structure with the expansion of the universe factored out. This motivates the use of comoving coordinates, which are defined to grow proportionally with the scale factor. If an object is moving only with the Hubble flow of the expanding universe, with no other motion, then it remains stationary in comoving coordinates. The comoving coordinates are the spatial coordinates in the FLRW metric.
Shape of the universe
[edit]The universe is a four-dimensional spacetime, but within a universe that obeys the cosmological principle, there is a natural choice of three-dimensional spatial surface. These are the surfaces on which observers who are stationary in comoving coordinates agree on the age of the universe. In a universe governed by special relativity, such surfaces would be hyperboloids, because relativistic time dilation means that rapidly receding distant observers' clocks are slowed, so that spatial surfaces must bend "into the future" over long distances. However, within general relativity, the shape of these comoving synchronous spatial surfaces is affected by gravity. Current observations are consistent with these spatial surfaces being geometrically flat (so that, for example, the angles of a triangle add up to 180 degrees).
Cosmological horizons
[edit]An expanding universe typically has a finite age. Light, and other particles, can have propagated only a finite distance. The comoving distance that such particles can have covered over the age of the universe is known as the particle horizon, and the region of the universe that lies within our particle horizon is known as the observable universe.
If the dark energy that is inferred to dominate the universe today is a cosmological constant, then the particle horizon converges to a finite value in the infinite future. This implies that the amount of the universe that we will ever be able to observe is limited. Many systems exist whose light can never reach us, because there is a cosmic event horizon induced by the repulsive gravity of the dark energy.
Within the study of the evolution of structure within the universe, a natural scale emerges, known as the Hubble horizon. Cosmological perturbations much larger than the Hubble horizon are not dynamical, because gravitational influences do not have time to propagate across them, while perturbations much smaller than the Hubble horizon are straightforwardly governed by Newtonian gravitational dynamics.
Consequences of cosmic expansion
[edit]Velocities and redshifts
[edit]An object's peculiar velocity is its velocity with respect to the comoving coordinate grid, i.e., with respect to the average expansion-associated motion of the surrounding material. It is a measure of how a particle's motion deviates from the Hubble flow of the expanding universe. The peculiar velocities of nonrelativistic particles decay as the universe expands, in inverse proportion with the cosmic scale factor. This can be understood as a self-sorting effect. A particle that is moving in some direction gradually overtakes the Hubble flow of cosmic expansion in that direction, asymptotically approaching material with the same velocity as its own.
More generally, the peculiar momenta of both relativistic and nonrelativistic particles decay in inverse proportion with the scale factor. For photons, this leads to the cosmological redshift. While the cosmological redshift is often explained as the stretching of photon wavelengths due to "expansion of space", it is more naturally viewed as a consequence of the Doppler effect.[3]
Temperature
[edit]The universe cools as it expands. This follows from the decay of particles' peculiar momenta, as discussed above. It can also be understood as adiabatic cooling. The temperature of ultrarelativistic fluids, often called "radiation" and including the cosmic microwave background, scales inversely with the scale factor (i.e. ). The temperature of nonrelativistic matter drops more sharply, scaling as the inverse square of the scale factor (i.e. ).
Density
[edit]The contents of the universe dilute as it expands. The number of particles within a comoving volume remains fixed (on average), while the volume expands. For nonrelativistic matter, this implies that the energy density drops as , where is the scale factor.
For ultrarelativistic particles ("radiation"), the energy density drops more sharply, as . This is because in addition to the volume dilution of the particle count, the energy of each particle (including the rest mass energy) also drops significantly due to the decay of peculiar momenta.
In general, we can consider a perfect fluid with pressure , where is the energy density. The parameter is the equation of state parameter. The energy density of such a fluid drops as
Nonrelativistic matter has while radiation has . For an exotic fluid with negative pressure, like dark energy, the energy density drops more slowly; if it remains constant in time. If , corresponding to phantom energy, the energy density grows as the universe expands.
Expansion history
[edit]
Cosmic inflation
[edit]Inflation is a period of accelerated expansion hypothesized to have occurred at a time of around 10−32 seconds. It would have been driven by the inflaton, a field that has a positive-energy false vacuum state. Inflation was originally proposed to explain the absence of exotic relics predicted by grand unified theories, such as magnetic monopoles, because the rapid expansion would have diluted such relics. It was subsequently realized that the accelerated expansion would also solve the horizon problem and the flatness problem. Additionally, quantum fluctuations during inflation would have created initial variations in the density of the universe, which gravity later amplified to yield the observed spectrum of matter density variations.[citation needed]
During inflation, the cosmic scale factor grew exponentially in time. In order to solve the horizon and flatness problems, inflation must have lasted long enough that the scale factor grew by at least a factor of e60 (about 1026).[citation needed]
Radiation epoch
[edit]The history of the universe after inflation but before a time of about 1 second is largely unknown.[20] However, the universe is known to have been dominated by ultrarelativistic Standard Model particles, conventionally called radiation, by the time of neutrino decoupling at about 1 second.[21] During radiation domination, cosmic expansion decelerated, with the scale factor growing proportionally with the square root of the time.
Matter epoch
[edit]Since radiation redshifts as the universe expands, eventually nonrelativistic matter came to dominate the energy density of the universe. This transition happened at a time of about 50 thousand years after the Big Bang. During the matter-dominated epoch, cosmic expansion also decelerated, with the scale factor growing as the 2/3 power of the time (). Also, gravitational structure formation is most efficient when nonrelativistic matter dominates, and this epoch is responsible for the formation of galaxies and the large-scale structure of the universe.
Dark energy
[edit]Around 3 billion years ago, at a time of about 11 billion years, dark energy is believed to have begun to dominate the energy density of the universe. This transition came about because dark energy does not dilute as the universe expands, instead maintaining a constant energy density. Similarly to inflation, dark energy drives accelerated expansion, such that the scale factor grows exponentially in time.
Measuring the expansion rate
[edit]
The most direct way to measure the expansion rate is to independently measure the recession velocities and the distances of distant objects, such as galaxies. The ratio between these quantities gives the Hubble rate, in accordance with Hubble's law. Typically, the distance is measured using a standard candle, which is an object or event for which the intrinsic brightness is known. The object's distance can then be inferred from the observed apparent brightness. Meanwhile, the recession speed is measured through the redshift. Hubble used this approach for his original measurement of the expansion rate, by measuring the brightness of Cepheid variable stars and the redshifts of their host galaxies. More recently, using Type Ia supernovae, the expansion rate was measured to be H0 = 73.24±1.74 (km/s)/Mpc.[22] This means that for every million parsecs of distance from the observer, recessional velocity of objects at that distance increases by about 73 kilometres per second (160,000 mph).
Supernovae are observable at such great distances that the light travel time therefrom can approach the age of the universe. Consequently, they can be used to measure not only the present-day expansion rate but also the expansion history. In work that was awarded the 2011 Nobel Prize in Physics, supernova observations were used to determine that cosmic expansion is accelerating in the present epoch.[23]
By assuming a cosmological model, e.g. the Lambda-CDM model, another possibility is to infer the present-day expansion rate from the sizes of the largest fluctuations seen in the cosmic microwave background. A higher expansion rate would imply a smaller characteristic size of CMB fluctuations, and vice versa. The Planck collaboration measured the expansion rate this way and determined H0 = 67.4±0.5 (km/s)/Mpc.[24] There is a disagreement between this measurement and the supernova-based measurements, known as the Hubble tension.
A third option proposed recently is to use information from gravitational wave events (especially those involving the merger of neutron stars, like GW170817), to measure the expansion rate.[25][26] Such measurements do not yet have the precision to resolve the Hubble tension.
In principle, the cosmic expansion history can also be measured by studying how redshifts, distances, fluxes, angular positions, and angular sizes of astronomical objects change over the course of the time that they are being observed. These effects are too small to have yet been detected. However, changes in redshift or flux could be observed by the Square Kilometre Array or Extremely Large Telescope in the mid-2030s.[27]
Conceptual considerations and misconceptions
[edit]Measuring distances in expanding space
[edit]At cosmological scales, the present universe conforms to Euclidean space, what cosmologists describe as geometrically flat, to within experimental error.[28]
Consequently, the rules of Euclidean geometry associated with Euclid's fifth postulate hold in the present universe in 3D space. It is, however, possible that the geometry of past 3D space could have been highly curved. The curvature of space is often modeled using a non-zero Riemann curvature tensor in curvature of Riemannian manifolds. Euclidean "geometrically flat" space has a Riemann curvature tensor of zero.
"Geometrically flat" space has three dimensions and is consistent with Euclidean space. However, spacetime has four dimensions; it is not flat according to Einstein's general theory of relativity. Einstein's theory postulates that "matter and energy curve spacetime, and there is enough matter and energy to provide for curvature."[29]
In part to accommodate such different geometries, the expansion of the universe is inherently general-relativistic. It cannot be modeled with special relativity alone: Though such models exist, they may be at fundamental odds with the observed interaction between matter and spacetime seen in the universe.
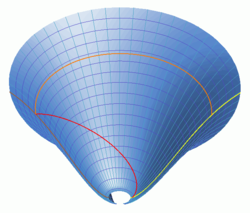
The images to the right show two views of spacetime diagrams that show the large-scale geometry of the universe according to the ΛCDM cosmological model. Two of the dimensions of space are omitted, leaving one dimension of space (the dimension that grows as the cone gets larger) and one of time (the dimension that proceeds "up" the cone's surface). The narrow circular end of the diagram corresponds to a cosmological time of 700 million years after the Big Bang, while the wide end is a cosmological time of 18 billion years, where one can see the beginning of the accelerating expansion as a splaying outward of the spacetime, a feature that eventually dominates in this model. The purple grid lines mark cosmological time at intervals of one billion years from the Big Bang. The cyan grid lines mark comoving distance at intervals of one billion light-years in the present era (less in the past and more in the future). The circular curling of the surface is an artifact of the embedding with no physical significance and is done for illustrative purposes; a flat universe does not curl back onto itself. (A similar effect can be seen in the tubular shape of the pseudosphere.)
The brown line on the diagram is the worldline of Earth (or more precisely its location in space, even before it was formed). The yellow line is the worldline of the most distant known quasar. The red line is the path of a light beam emitted by the quasar about 13 billion years ago and reaching Earth at the present day. The orange line shows the present-day distance between the quasar and Earth, about 28 billion light-years, which is a larger distance than the age of the universe multiplied by the speed of light, ct.
According to the equivalence principle of general relativity, the rules of special relativity are locally valid in small regions of spacetime that are approximately flat. In particular, light always travels locally at the speed c; in the diagram, this means, according to the convention of constructing spacetime diagrams, that light beams always make an angle of 45° with the local grid lines. It does not follow, however, that light travels a distance ct in a time t, as the red worldline illustrates. While it always moves locally at c, its time in transit (about 13 billion years) is not related to the distance traveled in any simple way, since the universe expands as the light beam traverses space and time. The distance traveled is thus inherently ambiguous because of the changing scale of the universe. Nevertheless, there are two distances that appear to be physically meaningful: the distance between Earth and the quasar when the light was emitted, and the distance between them in the present era (taking a slice of the cone along the dimension defined as the spatial dimension). The former distance is about 4 billion light-years, much smaller than ct, whereas the latter distance (shown by the orange line) is about 28 billion light-years, much larger than ct. In other words, if space were not expanding today, it would take 28 billion years for light to travel between Earth and the quasar, while if the expansion had stopped at the earlier time, it would have taken only 4 billion years.
The light took much longer than 4 billion years to reach us though it was emitted from only 4 billion light-years away. In fact, the light emitted towards Earth was actually moving away from Earth when it was first emitted; the metric distance to Earth increased with cosmological time for the first few billion years of its travel time, also indicating that the expansion of space between Earth and the quasar at the early time was faster than the speed of light. None of this behavior originates from a special property of metric expansion, but rather from local principles of special relativity integrated over a curved surface.
Topology of expanding space
[edit]Over time, the space that makes up the universe is expanding. The words 'space' and 'universe', sometimes used interchangeably, have distinct meanings in this context. Here 'space' is a mathematical concept that stands for the three-dimensional manifold into which our respective positions are embedded, while 'universe' refers to everything that exists, including the matter and energy in space, the extra dimensions that may be wrapped up in various strings, and the time through which various events take place. The expansion of space is in reference to this 3D manifold only; that is, the description involves no structures such as extra dimensions or an exterior universe.[30]
The ultimate topology of space is a posteriori – something that in principle must be observed – as there are no constraints that can simply be reasoned out (in other words there cannot be any a priori constraints) on how the space in which we live is connected or whether it wraps around on itself as a compact space. Though certain cosmological models such as Gödel's universe even permit bizarre worldlines that intersect with themselves, ultimately the question as to whether we are in something like a "Pac-Man universe", where if traveling far enough in one direction would allow one to simply end up back in the same place like going all the way around the surface of a balloon (or a planet like the Earth), is an observational question that is constrained as measurable or non-measurable by the universe's global geometry. At present, observations are consistent with the universe having infinite extent and being a simply connected space, though cosmological horizons limit our ability to distinguish between simple and more complicated proposals. The universe could be infinite in extent or it could be finite; but the evidence that leads to the inflationary model of the early universe also implies that the "total universe" is much larger than the observable universe. Thus any edges or exotic geometries or topologies would not be directly observable, since light has not reached scales on which such aspects of the universe, if they exist, are still allowed. For all intents and purposes, it is safe to assume that the universe is infinite in spatial extent, without edge or strange connectedness.[31]
Regardless of the overall shape of the universe, the question of what the universe is expanding into is one that does not require an answer, according to the theories that describe the expansion; the way we define space in our universe in no way requires additional exterior space into which it can expand, since an expansion of an infinite expanse can happen without changing the infinite extent of the expanse. All that is certain is that the manifold of space in which we live simply has the property that the distances between objects are getting larger as time goes on. This only implies the simple observational consequences associated with the metric expansion explored below. No "outside" or embedding in hyperspace is required for an expansion to occur. The visualizations often seen of the universe growing as a bubble into nothingness are misleading in that respect. There is no reason to believe there is anything "outside" the expanding universe into which the universe expands.
Even if the overall spatial extent is infinite and thus the universe cannot get any "larger", we still say that space is expanding because, locally, the characteristic distance between objects is increasing. As an infinite space grows, it remains infinite.
Density of universe during expansion
[edit]Despite being extremely dense when very young and during part of its early expansion – far denser than is usually required to form a black hole – the universe did not re-collapse into a black hole. This is because commonly used calculations for gravitational collapse are usually based upon objects of relatively constant size, such as stars, and do not apply to rapidly expanding space such as the Big Bang.[citation needed][dubious – discuss]
Effects of expansion on small scales
[edit]The expansion of space is sometimes described as a force that acts to push objects apart. Though this is an accurate description of the effect of the cosmological constant, it is not an accurate picture of the phenomenon of expansion in general.[32]

In addition to slowing the overall expansion, gravity causes local clumping of matter into stars and galaxies. Once objects are formed and bound by gravity, they "drop out" of the expansion and do not subsequently expand under the influence of the cosmological metric, there being no force compelling them to do so.
There is no difference between the inertial expansion of the universe and the inertial separation of nearby objects in a vacuum; the former is simply a large-scale extrapolation of the latter.
Once objects are bound by gravity, they no longer recede from each other. Thus, the Andromeda Galaxy, which is bound to the Milky Way Galaxy, is actually falling towards us and is not expanding away. Within the Local Group, the gravitational interactions have changed the inertial patterns of objects such that there is no cosmological expansion taking place. Beyond the Local Group, the inertial expansion is measurable, though systematic gravitational effects imply that larger and larger parts of space will eventually fall out of the "Hubble Flow" and end up as bound, non-expanding objects up to the scales of superclusters of galaxies. Such future events are predicted by knowing the precise way the Hubble Flow is changing as well as the masses of the objects to which we are being gravitationally pulled. Currently, the Local Group is being gravitationally pulled towards either the Shapley Supercluster or the "Great Attractor", with which we would eventually merge if dark energy were not acting.
A consequence of metric expansion being due to inertial motion is that a uniform local "explosion" of matter into a vacuum can be locally described by the FLRW geometry, the same geometry that describes the expansion of the universe as a whole and was also the basis for the simpler Milne universe, which ignores the effects of gravity. In particular, general relativity predicts that light will move at the speed c with respect to the local motion of the exploding matter, a phenomenon analogous to frame dragging.
The situation changes somewhat with the introduction of dark energy or a cosmological constant. A cosmological constant due to a vacuum energy density has the effect of adding a repulsive force between objects that is proportional (not inversely proportional) to distance. Unlike inertia it actively "pulls" on objects that have clumped together under the influence of gravity, and even on individual atoms. However, this does not cause the objects to grow steadily or to disintegrate; unless they are very weakly bound, they will simply settle into an equilibrium state that is slightly (undetectably) larger than it would otherwise have been. As the universe expands and the matter in it thins, the gravitational attraction decreases (since it is proportional to the density), while the cosmological repulsion increases. Thus, the ultimate fate of the ΛCDM universe is a near-vacuum expanding at an ever-increasing rate under the influence of the cosmological constant. However, gravitationally bound objects like the Milky Way do not expand, and the Andromeda Galaxy is moving fast enough towards us that it will still merge with the Milky Way in around 3 billion years.
Metric expansion and speed of light
[edit]At the end of the early universe's inflationary period, all the matter and energy in the universe was set on an inertial trajectory consistent with the equivalence principle and Einstein's general theory of relativity. This is when the precise and regular form of the universe's expansion had its origin (that is, matter in the universe is separating because it was separating in the past due to the inflaton field).[citation needed]
While special relativity prohibits objects from moving faster than light with respect to a local reference frame where spacetime can be treated as flat and unchanging, it does not apply to situations where spacetime curvature or evolution in time become important. These situations are described by general relativity, which allows the separation between two distant objects to increase faster than the speed of light, although the definition of "distance" here is somewhat different from that used in an inertial frame. The definition of distance used here is the summation or integration of local comoving distances, all done at constant local proper time. For example, galaxies that are farther than the Hubble radius, approximately 4.5 gigaparsecs or 14.7 billion light-years, away from us have a recession speed that is faster than the speed of light. Visibility of these objects depends on the exact expansion history of the universe. Light that is emitted today from galaxies beyond the more-distant cosmological event horizon, about 5 gigaparsecs or 16 billion light-years, will never reach us, although we can still see the light that these galaxies emitted in the past. Because of the high rate of expansion, it is also possible for a distance between two objects to be greater than the value calculated by multiplying the speed of light by the age of the universe. These details are a frequent source of confusion among amateurs and even professional physicists.[33] Due to the non-intuitive nature of the subject and what has been described by some as "careless" choices of wording, certain descriptions of the metric expansion of space and the misconceptions to which such descriptions can lead are an ongoing subject of discussion within the fields of education and communication of scientific concepts.[34][35][36][37]
Common analogies for cosmic expansion
[edit]The expansion of the universe is often illustrated with conceptual models where an expanding object is taken to represent expanding space. These models can be misleading to the extent that they give the false impression that expanding space must carry objects with it. In reality, the expansion of the universe can alternatively be thought of as corresponding only to the inertial motion of objects away from one another.
In the "ant on a rubber rope model" one imagines an ant (idealized as pointlike) crawling at a constant speed on a perfectly elastic rope that is constantly stretching. If we stretch the rope in accordance with the ΛCDM scale factor and think of the ant's speed as the speed of light, then this analogy is conceptually accurate – the ant's position over time will match the path of the red line on the embedding diagram above.
In the "rubber sheet model", one replaces the rope with a flat two-dimensional rubber sheet that expands uniformly in all directions. The addition of a second spatial dimension allows for the possibility of showing local perturbations of the spatial geometry by local curvature in the sheet.
In the "balloon model" the flat sheet is replaced by a spherical balloon that is inflated from an initial size of zero (representing the Big Bang). A balloon has positive Gaussian curvature, even though observations suggest that the real universe is spatially flat, but this inconsistency can be eliminated by making the balloon very large so that it is locally flat within the limits of observation. This analogy is potentially confusing since it could wrongly suggest that the Big Bang took place at the center of the balloon. In fact points off the surface of the balloon have no meaning, even if they were occupied by the balloon at an earlier time or will be occupied later.
In the "raisin bread model", one imagines a loaf of raisin bread expanding in an oven. The loaf (space) expands as a whole, but the raisins (gravitationally bound objects) do not expand; they merely move farther away from each other. This analogy has the disadvantage of wrongly implying that the expansion has a center and an edge.
See also
[edit]References
[edit]- ^ Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". The New York Times. Retrieved 21 February 2017.
- ^ Peacock (2008), arXiv:0809.4573
- ^ a b Bunn & Hogg, American Journal of Physics 77, pp. 688–694 (2009), arXiv:0808.1081
- ^ Lewis, Australian Physics 53(3), pp. 95–100 (2016), arXiv:1605.08634
- ^ Tipler, Monthly Notices of the Royal Astronomical Society 282(1), pp. 206–210 (1996).
- ^ Gibbons & Ellis, Classical and Quantum Gravity 31 (2), 025003 (2014), arXiv:1308.1852
- ^ Slipher, V. M. (1913). "The Radial Velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1 (8): 56–57. Bibcode:1913LowOB...2...56S.
- ^ "Vesto Slipher – American astronomer".
- ^ Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik. 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902. translated in Friedmann, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.
- ^ Steer, Ian (October 2012). "Who discovered Universe expansion?". Nature. 490 (7419): 176. arXiv:1212.1359. doi:10.1038/490176c. ISSN 1476-4687. PMID 23060180. S2CID 47038783.
- ^ Lemaître, Georges (1927). "Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques" [A homogeneous universe of constant mass and increasing radius accounting for the radial speed of extra-galactic nebulae]. Annales de la Société Scientifique de Bruxelles. A47: 49–59. Bibcode:1927ASSB...47...49L.
- ^ "Astronomer sleuth solves mystery of Big Cosmos discovery". Space.com. 14 November 2011.
- ^ Baade, W. (1944) "The resolution of Messier 32, NGC 205, and the central region of the Andromeda nebula". ApJ 100. pp. 137–146
- ^ Baade, W. (1956) "The period–luminosity relation of the Cepheids". PASP 68. pp. 5–16
- ^ Allen, Nick. "Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade". The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007. Retrieved 19 November 2011.
- ^ Trauger, J. T. (1994). ""The on-orbit performance of WFPC2"". Astrophysical Journal Letters. 435: L3. Bibcode:1994ApJ...435L...3T. doi:10.1086/187580.
- ^ Freedman, W. L. "The HST Key Project to Measure the Hubble Constant". www.stsci.edu. 813 Santa Barbara Street, Pasadena, California 91101.: Carnegie Observatories. Retrieved 17 June 2023.
((cite web)): CS1 maint: location (link) - ^ Riess, Adam G. (January 1995). ""Using Type IA supernova light curve shapes to measure the Hubble constant"". The Astrophysical Journal. 438: L17. arXiv:astro-ph/9410054. Bibcode:1995ApJ...438L..17R. doi:10.1086/187704. S2CID 118938423.
- ^ Spergel, D. N. (September 2003). "First-Year Wilkinson Microwave Anisotropy Probe (WMAP)1 Observations: Determination of Cosmological Parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
- ^ Allahverdi et al., Open J. Astrophys. 4, 1 (2021), arXiv:2006.16182
- ^ de Salas et al., Physical Review D. 92, 123534 (2015), arXiv:1511.00672
- ^ Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; Casertano, Stefano; Filippenko, Alexei V.; Tucker, Brad E.; Reid, Mark J.; Jones, David O.; Silverman, Jeffrey M.; Chornock, Ryan; Challis, Peter; Yuan, Wenlong; Brown, Peter J.; Foley, Ryan J. (2016). "A 2.4% Determination of the Local Value of the Hubble Constant". The Astrophysical Journal. 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ...826...56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.
- ^ "The Nobel Prize in Physics 2011". NobelPrize.org. Retrieved 17 June 2023.
- ^ Collaboration, Planck (2020). "Planck 2018 results. VI. Cosmological parameters". Astronomy & Astrophysics. 641: A6. arXiv:1807.06209. Bibcode:2020A&A...641A...6P. doi:10.1051/0004-6361/201833910. S2CID 119335614.
- ^ Lerner, Louise (22 October 2018). "Gravitational waves could soon provide measure of universe's expansion". Phys.org. Retrieved 22 October 2018.
- ^ Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). "A two per cent Hubble constant measurement from standard sirens within five years". Nature. 562 (7728): 545–547. arXiv:1712.06531. Bibcode:2018Natur.562..545C. doi:10.1038/s41586-018-0606-0. PMID 30333628. S2CID 52987203.
- ^ Bolejko, Krzysztof; Wang, Chengyi; Lewis, Geraint F. (2019). "Direct detection of the cosmic expansion: The redshift drift and the flux drift". arXiv:1907.04495 [astro-ph.CO].
- ^ Krauss, Lawrence M. (2012). A Universe from Nothing. Free Press. p. 82. ISBN 9781451624458.
- ^ Castelvecchi, Davide. "What Do You Mean, The Universe Is Flat? (Part I)". Scientific American Blog Network. Retrieved 17 June 2023.
- ^ Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press. p. 73. ISBN 9780691019338.
- ^ Rothstein, Dave (23 April 2003). "What is the universe expanding into?". Ask an Astronomer. Archived from the original on 8 June 2020. Retrieved 28 April 2017.
- ^ Pons, J. M.; Talavera, P. (2021). "On cosmological expansion and local physics". General Relativity and Gravitation. 53 (11): 105. arXiv:2011.01216. Bibcode:2021GReGr..53..105P. doi:10.1007/s10714-021-02874-4. S2CID 226236696.
- ^ Davis, Tamara M.; Lineweaver, Charles H. (2004). "Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the Universe". Publications of the Astronomical Society of Australia. 21 (1): 97–109. arXiv:astro-ph/0310808. Bibcode:2004PASA...21...97D. doi:10.1071/AS03040. ISSN 1323-3580. S2CID 13068122.
- ^ Whiting, Alan B. (2004). "The Expansion of Space: Free Particle Motion and the Cosmological Redshift". The Observatory. 124: 174. arXiv:astro-ph/0404095. Bibcode:2004Obs...124..174W.
- ^ Bunn, E. F.; Hogg, D. W. (2009). "The kinematic origin of the cosmological redshift". American Journal of Physics. 77 (8): 688–694. arXiv:0808.1081. Bibcode:2009AmJPh..77..688B. doi:10.1119/1.3129103. S2CID 1365918.
- ^ Baryshev, Yu. V. (2008). "Expanding Space: The Root of Conceptual Problems of the Cosmological Physics". Practical Cosmology. 2: 20–30. arXiv:0810.0153. Bibcode:2008pc2..conf...20B.
- ^ Peacock, J. A. (2008). "A diatribe on expanding space". arXiv:0809.4573 [astro-ph].
Printed references
[edit]- Eddington, Arthur. The Expanding Universe: Astronomy's 'Great Debate', 1900–1931. Press Syndicate of the University of Cambridge, 1933.
- Liddle, Andrew R. and Lyth, David H. Cosmological Inflation and Large-Scale Structure. Cambridge University Press, 2000.
- Lineweaver, Charles H. and Davis, Tamara M. "Misconceptions about the Big Bang", Scientific American, March 2005 (non-free content).
- Mook, Delo E. and Thomas Vargish. Inside Relativity. Princeton University Press, 1991.
External links
[edit]- Swenson, Jim, Answer to a question about the expanding universe Archived 11 January 2009 at the Wayback Machine
- Felder, Gary, "The Expanding universe".
- NASA's WMAP team offers an "Explanation of the universal expansion" at an elementary level.
- Hubble Tutorial from the University of Wisconsin Physics Department Archived 9 June 2014 at the Wayback Machine
- Expanding raisin bread from the University of Winnipeg: an illustration, but no explanation
- "Ant on a balloon" analogy to explain the expanding universe at "Ask an Astronomer" (the astronomer who provides this explanation is not specified).
| Background | |
|---|---|
| History of cosmological theories | |
| Past universe | |
| Present universe | |
| Future universe | |
| Components | |
| Structure formation | |
| Experiments | |